Repairable Systems Analysis Through Simulation
Having introduced some of the basic theory and terminology for repairable systems in Introduction to Repairable Systems, we will now examine the steps involved in the analysis of such complex systems. We will begin by examining system behavior through a sequence of discrete deterministic events and expand the analysis using discrete event simulation.
Simple Repairs
Deterministic View, Simple Series
To first understand how component failures and simple repairs affect the system and to visualize the steps involved, let's begin with a very simple deterministic example with two components, [math]\displaystyle{ A\,\! }[/math] and [math]\displaystyle{ B\,\! }[/math], in series.
Component [math]\displaystyle{ A\,\! }[/math] fails every 100 hours and component [math]\displaystyle{ B\,\! }[/math] fails every 120 hours. Both require 10 hours to get repaired. Furthermore, assume that the surviving component stops operating when the system fails (thus not aging). NOTE: When a failure occurs in certain systems, some or all of the system's components may or may not continue to accumulate operating time while the system is down. For example, consider a transmitter-satellite-receiver system. This is a series system and the probability of failure for this system is the probability that any of the subsystems fail. If the receiver fails, the satellite continues to operate even though the receiver is down. In this case, the continued aging of the components during the system inoperation must be taken into consideration, since this will affect their failure characteristics and have an impact on the overall system downtime and availability.
The system behavior during an operation from 0 to 300 hours would be as shown in the figure below.
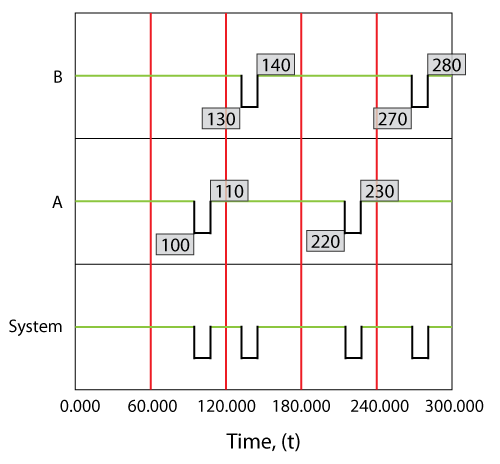
Specifically, component [math]\displaystyle{ A\,\! }[/math] would fail at 100 hours, causing the system to fail. After 10 hours, component [math]\displaystyle{ A\,\! }[/math] would be restored and so would the system. The next event would be the failure of component [math]\displaystyle{ B\,\! }[/math]. We know that component [math]\displaystyle{ B\,\! }[/math] fails every 120 hours (or after an age of 120 hours). Since a component does not age while the system is down, component [math]\displaystyle{ B\,\! }[/math] would have reached an age of 120 when the clock reaches 130 hours. Thus, component [math]\displaystyle{ B\,\! }[/math] would fail at 130 hours and be repaired by 140 and so forth. Overall in this scenario, the system would be failed for a total of 40 hours due to four downing events (two due to [math]\displaystyle{ A\,\! }[/math] and two due to [math]\displaystyle{ B\,\! }[/math] ). The overall system availability (average or mean availability) would be [math]\displaystyle{ 260/300=0.86667\,\! }[/math]. Point availability is the availability at a specific point time. In this deterministic case, the point availability would always be equal to 1 if the system is up at that time and equal to zero if the system is down at that time.
Operating Through System Failure
In the prior section we made the assumption that components do not age when the system is down. This assumption applies to most systems. However, under special circumstances, a unit may age even while the system is down. In such cases, the operating profile will be different from the one presented in the prior section. The figure below illustrates the case where the components operate continuously, regardless of the system status.
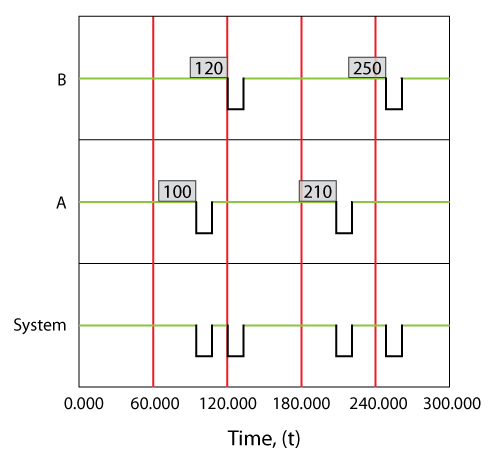
Effects of Operating Through Failure
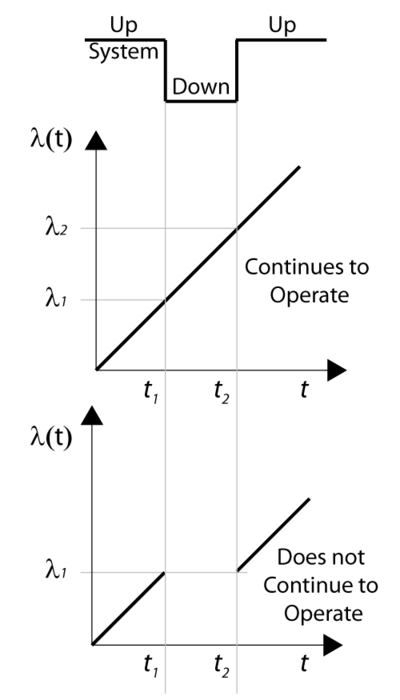
Consider a component with an increasing failure rate, as shown in the figure below. In the case that the component continues to operate through system failure, then when the system fails at [math]\displaystyle{ {{t}_{1}}\,\! }[/math] the surviving component's failure rate will be [math]\displaystyle{ {{\lambda }_{1}}\,\! }[/math], as illustrated in figure below. When the system is restored at [math]\displaystyle{ {{t}_{2}}\,\! }[/math], the component would have aged by [math]\displaystyle{ {{t}_{2}}-{{t}_{1}}\,\! }[/math] and its failure rate would now be [math]\displaystyle{ {{\lambda }_{2}}\,\! }[/math].
In the case of a component that does not operate through failure, then the surviving component would be at the same failure rate, [math]\displaystyle{ {{\lambda }_{1}},\,\! }[/math] when the system resumes operation.
Deterministic View, Simple Parallel
Consider the following system where [math]\displaystyle{ A\,\! }[/math] fails every 100, [math]\displaystyle{ B\,\! }[/math] every 120, [math]\displaystyle{ C\,\! }[/math] every 140 and [math]\displaystyle{ D\,\! }[/math] every 160 time units. Each takes 10 time units to restore. Furthermore, assume that components do not age when the system is down.
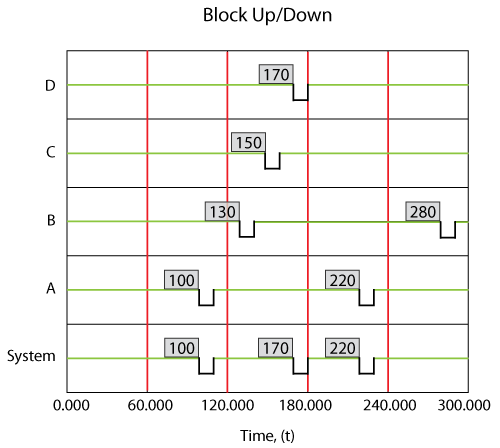
A deterministic system view is shown in the figure below. The sequence of events is as follows:
- At 100, [math]\displaystyle{ A\,\! }[/math] fails and is repaired by 110. The system is failed.
- At 130, [math]\displaystyle{ B\,\! }[/math] fails and is repaired by 140. The system continues to operate.
- At 150, [math]\displaystyle{ C\,\! }[/math] fails and is repaired by 160. The system continues to operate.
- At 170, [math]\displaystyle{ D\,\! }[/math] fails and is repaired by 180. The system is failed.
- At 220, [math]\displaystyle{ A\,\! }[/math] fails and is repaired by 230. The system is failed.
- At 280, [math]\displaystyle{ B\,\! }[/math] fails and is repaired by 290. The system continues to operate.
- End at 300.
Additional Notes
It should be noted that we are dealing with these events deterministically in order to better illustrate the methodology. When dealing with deterministic events, it is possible to create a sequence of events that one would not expect to encounter probabilistically. One such example consists of two units in series that do not operate through failure but both fail at exactly 100, which is highly unlikely in a real-world scenario. In this case, the assumption is that one of the events must occur at least an infinitesimal amount of time ( [math]\displaystyle{ dt)\,\! }[/math] before the other. Probabilistically, this event is extremely rare, since both randomly generated times would have to be exactly equal to each other, to 15 decimal points. In the rare event that this happens, BlockSim would pick the unit with the lowest ID value as the first failure. BlockSim assigns a unique numerical ID when each component is created. These can be viewed by selecting the Show Block ID option in the Diagram Options window.
Deterministic Views of More Complex Systems
Even though the examples presented are fairly simplistic, the same approach can be repeated for larger and more complex systems. The reader can easily observe/visualize the behavior of more complex systems in BlockSim using the Up/Down plots. These are the same plots used in this chapter. It should be noted that BlockSim makes these plots available only when a single simulation run has been performed for the analysis (i.e., Number of Simulations = 1). These plots are meaningless when doing multiple simulations because each run will yield a different plot.
Probabilistic View, Simple Series
In a probabilistic case, the failures and repairs do not happen at a fixed time and for a fixed duration, but rather occur randomly and based on an underlying distribution, as shown in the following figures.
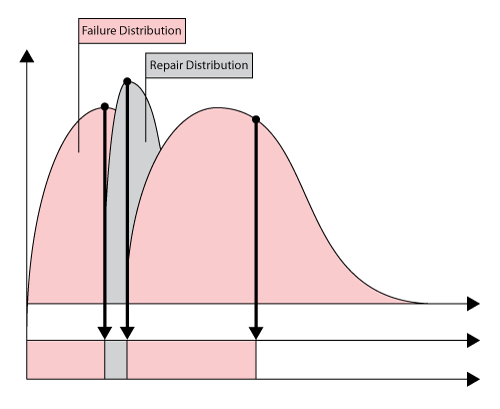
We use discrete event simulation in order to analyze (understand) the system behavior. Discrete event simulation looks at each system/component event very similarly to the way we looked at these events in the deterministic example. However, instead of using deterministic (fixed) times for each event occurrence or duration, random times are used. These random times are obtained from the underlying distribution for each event. As an example, consider an event following a 2-parameter Weibull distribution. The cdf of the 2-parameter Weibull distribution is given by:
- [math]\displaystyle{ F(T)=1-{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}}\,\! }[/math]
The Weibull reliability function is given by:
- [math]\displaystyle{ \begin{align} R(T)= & 1-F(t) \\ = & {{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}} \end{align}\,\! }[/math]
Then, to generate a random time from a Weibull distribution with a given [math]\displaystyle{ \eta \,\! }[/math] and [math]\displaystyle{ \beta \,\! }[/math], a uniform random number from 0 to 1, [math]\displaystyle{ {{U}_{R}}[0,1]\,\! }[/math], is first obtained. The random time from a Weibull distribution is then obtained from:
- [math]\displaystyle{ {{T}_{R}}=\eta \cdot {{\left\{ -\ln \left[ {{U}_{R}}[0,1] \right] \right\}}^{\tfrac{1}{\beta }}}\,\! }[/math]
To obtain a conditional time, the Weibull conditional reliability function is given by:
- [math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)}=\frac{{{e}^{-{{\left( \tfrac{T+t}{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}}}\,\! }[/math]
Or:
- [math]\displaystyle{ R(t|T)={{e}^{-\left[ {{\left( \tfrac{T+t}{\eta } \right)}^{\beta }}-{{\left( \tfrac{T}{\eta } \right)}^{\beta }} \right]}}\,\! }[/math]
The random time would be the solution for [math]\displaystyle{ t\,\! }[/math] for [math]\displaystyle{ R(t|T)={{U}_{R}}[0,1]\,\! }[/math].
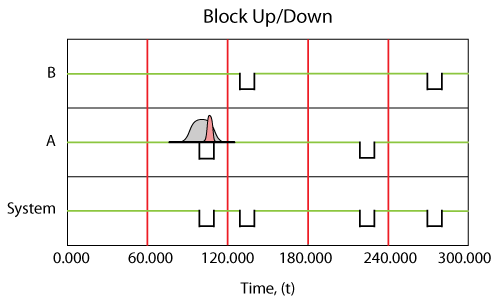
To illustrate the sequence of events, assume a single block with a failure and a repair distribution. The first event, [math]\displaystyle{ {{E}_{{{F}_{1}}}}\,\! }[/math], would be the failure of the component. Its first time-to-failure would be a random number drawn from its failure distribution, [math]\displaystyle{ {{T}_{{{F}_{1}}}}\,\! }[/math]. Thus, the first failure event, [math]\displaystyle{ {{E}_{{{F}_{1}}}}\,\! }[/math], would be at [math]\displaystyle{ {{T}_{{{F}_{1}}}}\,\! }[/math]. Once failed, the next event would be the repair of the component, [math]\displaystyle{ {{E}_{{{R}_{1}}}}\,\! }[/math]. The time to repair the component would now be drawn from its repair distribution, [math]\displaystyle{ {{T}_{{{R}_{1}}}}\,\! }[/math]. The component would be restored by time [math]\displaystyle{ {{T}_{{{F}_{1}}}}+{{T}_{{{R}_{1}}}}\,\! }[/math]. The next event would now be the second failure of the component after the repair, [math]\displaystyle{ {{E}_{{{F}_{2}}}}\,\! }[/math]. This event would occur after a component operating time of [math]\displaystyle{ {{T}_{{{F}_{2}}}}\,\! }[/math] after the item is restored (again drawn from the failure distribution), or at [math]\displaystyle{ {{T}_{{{F}_{1}}}}+{{T}_{{{R}_{1}}}}+{{T}_{{{F}_{2}}}}\,\! }[/math]. This process is repeated until the end time. It is important to note that each run will yield a different sequence of events due to the probabilistic nature of the times. To arrive at the desired result, this process is repeated many times and the results from each run (simulation) are recorded. In other words, if we were to repeat this 1,000 times, we would obtain 1,000 different values for [math]\displaystyle{ {{E}_{{{F}_{1}}}}\,\! }[/math], or [math]\displaystyle{ \left[ {{E}_{{{F}_{{{1}_{1}}}}}},{{E}_{{{F}_{{{1}_{2}}}}}},...,{{E}_{{{F}_{{{1}_{1,000}}}}}} \right]\,\! }[/math]. The average of these values, [math]\displaystyle{ \left( \tfrac{1}{1000}\underset{i=1}{\overset{1,000}{\mathop{\sum }}}\,{{E}_{{{F}_{{{1}_{i}}}}}} \right)\,\! }[/math], would then be the average time to the first event, [math]\displaystyle{ {{E}_{{{F}_{1}}}}\,\! }[/math], or the mean time to first failure (MTTFF) for the component. Obviously, if the component were to be 100% renewed after each repair, then this value would also be the same for the second failure, etc.
General Simulation Results
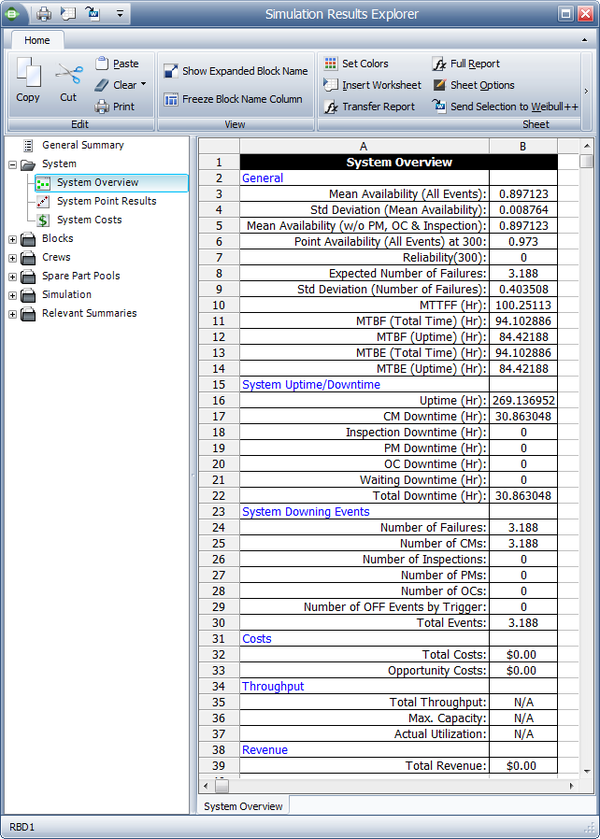
To further illustrate this, assume that components A and B in the prior example had normal failure and repair distributions with their means equal to the deterministic values used in the prior example and standard deviations of 10 and 1 respectively. That is, [math]\displaystyle{ {{F}_{A}}\tilde{\ }N(100,10),\,\! }[/math] [math]\displaystyle{ {{F}_{B}}\tilde{\ }N(120,10),\,\! }[/math] [math]\displaystyle{ {{R}_{A}}={{R}_{B}}\tilde{\ }N(10,1)\,\! }[/math]. The settings for components C and D are not changed. Obviously, given the probabilistic nature of the example, the times to each event will vary. If one were to repeat this [math]\displaystyle{ X\,\! }[/math] number of times, one would arrive at the results of interest for the system and its components. Some of the results for this system and this example, over 1,000 simulations, are provided in the figure below and explained in the next sections.
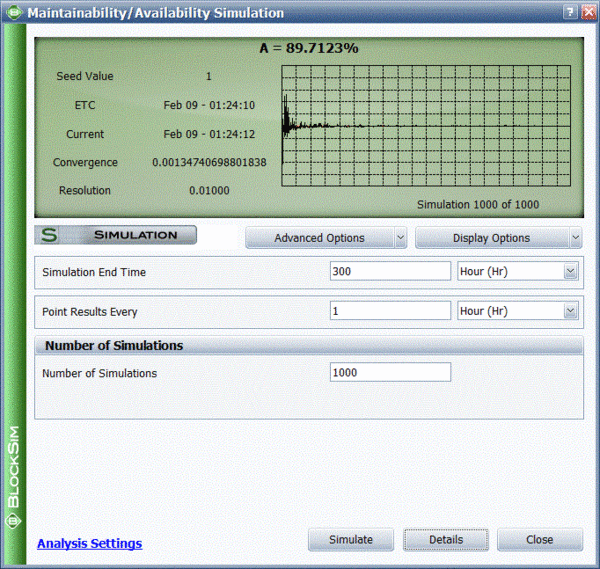
The simulation settings are shown in the figure below.
General
Mean Availability (All Events), [math]\displaystyle{ {{\overline{A}}_{ALL}}\,\! }[/math]
This is the mean availability due to all downing events, which can be thought of as the operational availability. It is the ratio of the system uptime divided by the total simulation time (total time). For this example:
- [math]\displaystyle{ \begin{align} {{\overline{A}}_{ALL}}= & \frac{Uptime}{TotalTime} \\ = & \frac{269.137}{300} \\ = & 0.8971 \end{align}\,\! }[/math]
Std Deviation (Mean Availability)
This is the standard deviation of the mean availability of all downing events for the system during the simulation.
Mean Availability (w/o PM, OC & Inspection), [math]\displaystyle{ {{\overline{A}}_{CM}}\,\! }[/math]
This is the mean availability due to failure events only and it is 0.971 for this example. Note that for this case, the mean availability without preventive maintenance, on condition maintenance and inspection is identical to the mean availability for all events. This is because no preventive maintenance actions or inspections were defined for this system. We will discuss the inclusion of these actions in later sections.
Downtimes caused by PM and inspections are not included. However, if the PM or inspection action results in the discovery of a failure, then these times are included. As an example, consider a component that has failed but its failure is not discovered until the component is inspected. Then the downtime from the time failed to the time restored after the inspection is counted as failure downtime, since the original event that caused this was the component's failure.
Point Availability (All Events), [math]\displaystyle{ A\left( t \right)\,\! }[/math]
This is the probability that the system is up at time [math]\displaystyle{ t\,\! }[/math]. As an example, to obtain this value at [math]\displaystyle{ t\,\! }[/math] = 300, a special counter would need to be used during the simulation. This counter is increased by one every time the system is up at 300 hours. Thus, the point availability at 300 would be the times the system was up at 300 divided by the number of simulations. For this example, this is 0.930, or 930 times out of the 1000 simulations the system was up at 300 hours.
Reliability (Fail Events), [math]\displaystyle{ R(t)\,\! }[/math]
This is the probability that the system has not failed by time [math]\displaystyle{ t\,\! }[/math]. This is similar to point availability with the major exception that it only looks at the probability that the system did not have a single failure. Other (non-failure) downing events are ignored. During the simulation, a special counter again must be used. This counter is increased by one (once in each simulation) if the system has had at least one failure up to 300 hours. Thus, the reliability at 300 would be the number of times the system did not fail up to 300 divided by the number of simulations. For this example, this is 0 because the system failed prior to 300 hours 1000 times out of the 1000 simulations.
It is very important to note that this value is not always the same as the reliability computed using the analytical methods, depending on the redundancy present. The reason that it may differ is best explained by the following scenario:
Assume two units in parallel. The analytical system reliability, which does not account for repairs, is the probability that both units fail. In this case, when one unit goes down, it does not get repaired and the system fails after the second unit fails. In the case of repairs, however, it is possible for one of the two units to fail and get repaired before the second unit fails. Thus, when the second unit fails, the system will still be up due to the fact that the first unit was repaired.
Expected Number of Failures, [math]\displaystyle{ {{N}_{F}}\,\! }[/math]
This is the average number of system failures. The system failures (not downing events) for all simulations are counted and then averaged. For this case, this is 3.188, which implies that a total of 3,188 system failure events occurred over 1000 simulations. Thus, the expected number of system failures for one run is 3.188. This number includes all failures, even those that may have a duration of zero.
Std Deviation (Number of Failures)
This is the standard deviation of the number of failures for the system during the simulation.
MTTFF
MTTFF is the mean time to first failure for the system. This is computed by keeping track of the time at which the first system failure occurred for each simulation. MTTFF is then the average of these times. This may or may not be identical to the MTTF obtained in the analytical solution for the same reasons as those discussed in the Point Reliability section. For this case, this is 100.2511. This is fairly obvious for this case since the mean of one of the components in series was 100 hours.
It is important to note that for each simulation run, if a first failure time is observed, then this is recorded as the system time to first failure. If no failure is observed in the system, then the simulation end time is used as a right censored (suspended) data point. MTTFF is then computed using the total operating time until the first failure divided by the number of observed failures (constant failure rate assumption). Furthermore, and if the simulation end time is much less than the time to first failure for the system, it is also possible that all data points are right censored (i.e., no system failures were observed). In this case, the MTTFF is again computed using a constant failure rate assumption, or:
- [math]\displaystyle{ MTTFF=\frac{2\cdot ({{T}_{S}})\cdot N}{\chi _{0.50;2}^{2}}\,\! }[/math]
where [math]\displaystyle{ {{T}_{S}}\,\! }[/math] is the simulation end time and [math]\displaystyle{ N\,\! }[/math] is the number of simulations. One should be aware that this formulation may yield unrealistic (or erroneous) results if the system does not have a constant failure rate. If you are trying to obtain an accurate (realistic) estimate of this value, then your simulation end time should be set to a value that is well beyond the MTTF of the system (as computed analytically). As a general rule, the simulation end time should be at least three times larger than the MTTF of the system.
MTBF (Total Time)
This is the mean time between failures for the system based on the total simulation time and the expected number of system failures. For this example:
- [math]\displaystyle{ \begin{align} MTBF (Total Time)= & \frac{TotalTime}{{N}_{F}} \\ = & \frac{300}{3.188} \\ = & 94.102886 \end{align}\,\! }[/math]
MTBF (Uptime)
This is the mean time between failures for the system, considering only the time that the system was up. This is calculated by dividing system uptime by the expected number of system failures. You can also think of this as the mean uptime. For this example:
- [math]\displaystyle{ \begin{align} MTBF (Uptime)= & \frac{Uptime}{{N}_{F}} \\ = & \frac{269.136952}{3.188} \\ = & 84.42188 \end{align}\,\! }[/math]
MTBE (Total Time)
This is the mean time between all downing events for the system, based on the total simulation time and including all system downing events. This is calculated by dividing the simulation run time by the number of downing events ([math]\displaystyle{ {{N}_{AL{{L}_{Down}}}}\,\! }[/math]).
MTBE (Uptime)
his is the mean time between all downing events for the system, considering only the time that the system was up. This is calculated by dividing system uptime by the number of downing events ([math]\displaystyle{ {{N}_{AL{{L}_{Down}}}}\,\! }[/math]).
System Uptime/Downtime
Uptime, [math]\displaystyle{ {{T}_{UP}}\,\! }[/math]
This is the average time the system was up and operating. This is obtained by taking the sum of the uptimes for each simulation and dividing it by the number of simulations. For this example, the uptime is 269.137. To compute the Operational Availability, [math]\displaystyle{ {{A}_{o}},\,\! }[/math] for this system, then:
- [math]\displaystyle{ {{A}_{o}}=\frac{{{T}_{UP}}}{{{T}_{S}}}\,\! }[/math]
CM Downtime, [math]\displaystyle{ {{T}_{C{{M}_{Down}}}}\,\! }[/math]
This is the average time the system was down for corrective maintenance actions (CM) only. This is obtained by taking the sum of the CM downtimes for each simulation and dividing it by the number of simulations. For this example, this is 30.863. To compute the Inherent Availability, [math]\displaystyle{ {{A}_{I}},\,\! }[/math] for this system over the observed time (which may or may not be steady state, depending on the length of the simulation), then:
- [math]\displaystyle{ {{A}_{I}}=\frac{{{T}_{S}}-{{T}_{C{{M}_{Down}}}}}{{{T}_{S}}}\,\! }[/math]
Inspection Downtime
This is the average time the system was down due to inspections. This is obtained by taking the sum of the inspection downtimes for each simulation and dividing it by the number of simulations. For this example, this is zero because no inspections were defined.
PM Downtime, [math]\displaystyle{ {{T}_{P{{M}_{Down}}}}\,\! }[/math]
This is the average time the system was down due to preventive maintenance (PM) actions. This is obtained by taking the sum of the PM downtimes for each simulation and dividing it by the number of simulations. For this example, this is zero because no PM actions were defined.
OC Downtime, [math]\displaystyle{ {{T}_{O{{C}_{Down}}}}\,\! }[/math]
This is the average time the system was down due to on-condition maintenance (PM) actions. This is obtained by taking the sum of the OC downtimes for each simulation and dividing it by the number of simulations. For this example, this is zero because no OC actions were defined.
Waiting Downtime, [math]\displaystyle{ {{T}_{W{{ait}_{Down}}}}\,\! }[/math]
This is the amount of time that the system was down due to crew and spare part wait times or crew conflict times. For this example, this is zero because no crews or spare part pools were defined.
Total Downtime, [math]\displaystyle{ {{T}_{Down}}\,\! }[/math]
This is the downtime due to all events. In general, one may look at this as the sum of the above downtimes. However, this is not always the case. It is possible to have actions that overlap each other, depending on the options and settings for the simulation. Furthermore, there are other events that can cause the system to go down that do not get counted in any of the above categories. As an example, in the case of standby redundancy with a switch delay, if the settings are to reactivate the failed component after repair, the system may be down during the switch-back action. This downtime does not fall into any of the above categories but it is counted in the total downtime.
For this example, this is identical to [math]\displaystyle{ {{T}_{C{{M}_{Down}}}}\,\! }[/math].
System Downing Events
System downing events are events associated with downtime. Note that events with zero duration will appear in this section only if the task properties specify that the task brings the system down or if the task properties specify that the task brings the item down and the item’s failure brings the system down.
Number of Failures, [math]\displaystyle{ {{N}_{{{F}_{Down}}}}\,\! }[/math]
This is the average number of system downing failures. Unlike the Expected Number of Failures, [math]\displaystyle{ {{N}_{F}},\,\! }[/math] this number does not include failures with zero duration. For this example, this is 3.188.
Number of CMs, [math]\displaystyle{ {{N}_{C{{M}_{Down}}}}\,\! }[/math]
This is the number of corrective maintenance actions that caused the system to fail. It is obtained by taking the sum of all CM actions that caused the system to fail divided by the number of simulations. It does not include CM events of zero duration. For this example, this is 3.188. Note that this may differ from the Number of Failures, [math]\displaystyle{ {{N}_{{{F}_{Down}}}}\,\! }[/math]. An example would be a case where the system has failed, but due to other settings for the simulation, a CM is not initiated (e.g., an inspection is needed to initiate a CM).
Number of Inspections, [math]\displaystyle{ {{N}_{{{I}_{Down}}}}\,\! }[/math]
This is the number of inspection actions that caused the system to fail. It is obtained by taking the sum of all inspection actions that caused the system to fail divided by the number of simulations. It does not include inspection events of zero duration. For this example, this is zero.
Number of PMs, [math]\displaystyle{ {{N}_{P{{M}_{Down}}}}\,\! }[/math]
This is the number of PM actions that caused the system to fail. It is obtained by taking the sum of all PM actions that caused the system to fail divided by the number of simulations. It does not include PM events of zero duration. For this example, this is zero.
Number of OCs, [math]\displaystyle{ {{N}_{O{{C}_{Down}}}}\,\! }[/math]
This is the number of OC actions that caused the system to fail. It is obtained by taking the sum of all OC actions that caused the system to fail divided by the number of simulations. It does not include OC events of zero duration. For this example, this is zero.
Number of OFF Events by Trigger, [math]\displaystyle{ {{N}_{O{{FF}_{Down}}}}\,\! }[/math]
This is the total number of events where the system is turned off by state change triggers. An OFF event is not a system failure but it may be included in system reliability calculations. For this example, this is zero.
Total Events, [math]\displaystyle{ {{N}_{AL{{L}_{Down}}}}\,\! }[/math]
This is the total number of system downing events. It also does not include events of zero duration. It is possible that this number may differ from the sum of the other listed events. As an example, consider the case where a failure does not get repaired until an inspection, but the inspection occurs after the simulation end time. In this case, the number of inspections, CMs and PMs will be zero while the number of total events will be one.
Costs and Throughput
Cost and throughput results are discussed in later sections.
Note About Overlapping Downing Events
It is important to note that two identical system downing events (that are continuous or overlapping) may be counted and viewed differently. As shown in Case 1 of the following figure, two overlapping failure events are counted as only one event from the system perspective because the system was never restored and remained in the same down state, even though that state was caused by two different components. Thus, the number of downing events in this case is one and the duration is as shown in CM system. In the case that the events are different, as shown in Case 2 of the figure below, two events are counted, the CM and the PM. However, the downtime attributed to each event is different from the actual time of each event. In this case, the system was first down due to a CM and remained in a down state due to the CM until that action was over. However, immediately upon completion of that action, the system remained down but now due to a PM action. In this case, only the PM action portion that kept the system down is counted.

System Point Results
The system point results, as shown in the figure below, shows the Point Availability (All Events), [math]\displaystyle{ A\left( t \right)\,\! }[/math], and Point Reliability, [math]\displaystyle{ R(t)\,\! }[/math], as defined in the previous section. These are computed and returned at different points in time, based on the number of intervals selected by the user. Additionally, this window shows [math]\displaystyle{ (1-A(t))\,\! }[/math], [math]\displaystyle{ (1-R(t))\,\! }[/math], [math]\displaystyle{ \text{Labor Cost(t)}\,\! }[/math],[math]\displaystyle{ \text{Part Cost(t)}\,\! }[/math], [math]\displaystyle{ Cost(t)\,\! }[/math], [math]\displaystyle{ Mean\,\! }[/math] [math]\displaystyle{ A(t)\,\! }[/math], [math]\displaystyle{ Mean\,\! }[/math] [math]\displaystyle{ A({{t}_{i}}-{{t}_{i-1}})\,\! }[/math], [math]\displaystyle{ System\,\! }[/math], [math]\displaystyle{ Failures(t)\,\! }[/math], [math]\displaystyle{ \text{System Off Events by Trigger(t)}\,\! }[/math] and [math]\displaystyle{ Throughput(t)\,\! }[/math].
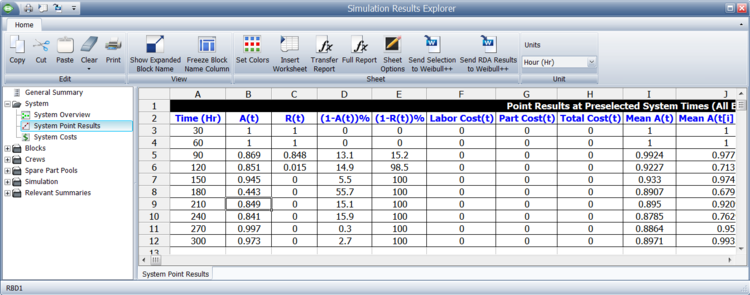
The number of intervals shown is based on the increments set. In this figure, the number of increments set was 300, which implies that the results should be shown every hour. The results shown in this figure are for 10 increments, or shown every 30 hours.
Results by Component
Simulation results for each component can also be viewed. The figure below shows the results for component A. These results are explained in the sections that follow.
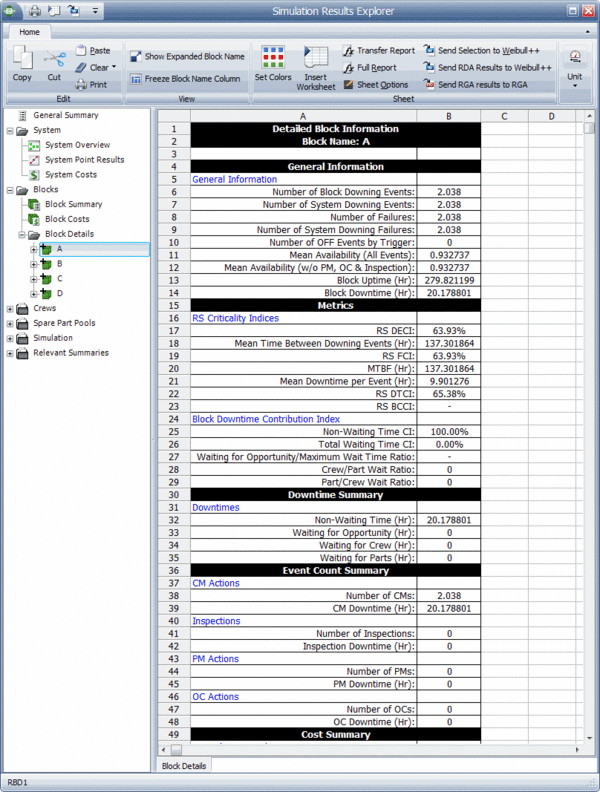
General Information
Number of Block Downing Events, [math]\displaystyle{ Componen{{t}_{NDE}}\,\! }[/math]
This the number of times the component went down (failed). It includes all downing events.
Number of System Downing Events, [math]\displaystyle{ Componen{{t}_{NSDE}}\,\! }[/math]
This is the number of times that this component's downing caused the system to be down. For component [math]\displaystyle{ A\,\! }[/math], this is 2.038. Note that this value is the same in this case as the number of component failures, since the component A is reliability-wise in series with components D and components B, C. If this were not the case (e.g., if they were in a parallel configuration, like B and C), this value would be different.
Number of Failures, [math]\displaystyle{ Componen{{t}_{NF}}\,\! }[/math]
This is the number of times the component failed and does not include other downing events. Note that this could also be interpreted as the number of spare parts required for CM actions for this component. For component [math]\displaystyle{ A\,\! }[/math], this is 2.038.
Number of System Downing Failures, [math]\displaystyle{ Componen{{t}_{NSDF}}\,\! }[/math]
This is the number of times that this component's failure caused the system to be down. Note that this may be different from the Number of System Downing Events. It only counts the failure events that downed the system and does not include zero duration system failures.
Number of OFF events by Trigger, [math]\displaystyle{ Componen{{t}_{OFF}}\,\! }[/math]
The total number of events where the block is turned off by state change triggers. An OFF event is not a failure but it may be included in system reliability calculations.
Mean Availability (All Events), [math]\displaystyle{ {{\overline{A}}_{AL{{L}_{Component}}}}\,\! }[/math]
This has the same definition as for the system with the exception that this accounts only for the component.
Mean Availability (w/o PM, OC & Inspection), [math]\displaystyle{ {{\overline{A}}_{C{{M}_{Component}}}}\,\! }[/math]
The mean availability of all downing events for the block, not including preventive, on condition or inspection tasks, during the simulation.
Block Uptime, [math]\displaystyle{ {{T}_{Componen{{t}_{UP}}}}\,\! }[/math]
This is tThe total amount of time that the block was up (i.e., operational) during the simulation. For component [math]\displaystyle{ A\,\! }[/math], this is 279.8212.
Block Downtime, [math]\displaystyle{ {{T}_{Componen{{t}_{Down}}}}\,\! }[/math]
This is the average time the component was down for any reason. For component [math]\displaystyle{ A\,\! }[/math], this is 20.1788.
Block Downtime shows the total amount of time that the block was down (i.e., not operational) during the simulation.
Metrics
RS DECI
The ReliaSoft Downing Event Criticality Index for the block. This is a relative index showing the percentage of times that a downing event of the block caused the system to go down (i.e., the number of system downing events caused by the block divided by the total number of system downing events). For component [math]\displaystyle{ A\,\! }[/math], this is 63.93%. This implies that 63.93% of the times that the system went down, the system failure was due to the fact that component [math]\displaystyle{ A\,\! }[/math] went down. This is obtained from:
- [math]\displaystyle{ \begin{align} RSDECI=\frac{Componen{{t}_{NSDE}}}{{{N}_{AL{{L}_{Down}}}}} \end{align}\,\! }[/math]
Mean Time Between Downing Events
This is the mean time between downing events of the component, which is computed from:
- [math]\displaystyle{ MTBDE=\frac{{{T}_{Componen{{t}_{UP}}}}}{Componen{{t}_{NDE}}}\,\! }[/math]
For component [math]\displaystyle{ A\,\! }[/math], this is 137.3019.
RS FCI
ReliaSoft's Failure Criticality Index (RS FCI) is a relative index showing the percentage of times that a failure of this component caused a system failure. For component [math]\displaystyle{ A\,\! }[/math], this is 63.93%. This implies that 63.93% of the times that the system failed, it was due to the fact that component [math]\displaystyle{ A\,\! }[/math] failed. This is obtained from:
- [math]\displaystyle{ \begin{align} RSFCI=\frac{Componen{{t}_{NSDF}}+{{F}_{ZD}}}{{{N}_{F}}} \end{align}\,\! }[/math]
[math]\displaystyle{ {{F}_{ZD}}\,\! }[/math] is a special counter of system failures not included in [math]\displaystyle{ Componen{{t}_{NSDF}}\,\! }[/math]. This counter is not explicitly shown in the results but is maintained by the software. The reason for this counter is the fact that zero duration failures are not counted in [math]\displaystyle{ Componen{{t}_{NSDF}}\,\! }[/math] since they really did not down the system. However, these zero duration failures need to be included when computing RS FCI.
It is important to note that for both RS DECI and RS FCI, and if overlapping events are present, the component that caused the system event gets credited with the system event. Subsequent component events that do not bring the system down (since the system is already down) do not get counted in this metric.
MTBF, [math]\displaystyle{ MTB{{F}_{C}}\,\! }[/math]
Mean time between failures is the mean (average) time between failures of this component, in real clock time. This is computed from:
- [math]\displaystyle{ MTB{{F}_{C}}=\frac{{{T}_{S}}-CFDowntime}{Componen{{t}_{NF}}}\,\! }[/math]
[math]\displaystyle{ CFDowntime\,\! }[/math] is the downtime of the component due to failures only (without PM, OC and inspection). The discussion regarding what is a failure downtime that was presented in the section explaining Mean Availability (w/o PM & Inspection) also applies here. For component [math]\displaystyle{ A\,\! }[/math], this is 137.3019. Note that this value could fluctuate for the same component depending on the simulation end time. As an example, consider the deterministic scenario for this component. It fails every 100 hours and takes 10 hours to repair. Thus, it would be failed at 100, repaired by 110, failed at 210 and repaired by 220. Therefore, its uptime is 280 with two failure events, MTBF = 280/2 = 140. Repeating the same scenario with an end time of 330 would yield failures at 100, 210 and 320. Thus, the uptime would be 300 with three failures, or MTBF = 300/3 = 100. Note that this is not the same as the MTTF (mean time to failure), commonly referred to as MTBF by many practitioners.
Mean Downtime per Event, [math]\displaystyle{ MDPE\,\! }[/math]
Mean downtime per event is the average downtime for a component event. This is computed from:
- [math]\displaystyle{ MDPE=\frac{{{T}_{Componen{{t}_{Down}}}}}{Componen{{t}_{NDE}}}\,\! }[/math]
RS DTCI
The ReliaSoft Downtime Criticality Index for the block. This is a relative index showing the contribution of the block to the system’s downtime (i.e., the system downtime caused by the block divided by the total system downtime).
RS BCCI
The ReliaSoft Block Cost Criticality Index for the block. This is a relative index showing the contribution of the block to the total costs (i.e., the total block costs divided by the total costs).
Non-Waiting Time CI
A relative index showing the contribution of repair times to the block’s total downtime. (The ratio of the time that the crew is actively working on the item to the total down time).
Total Waiting Time CI
A relative index showing the contribution of wait factor times to the block’s total downtime. Wait factors include crew conflict times, crew wait times and spare part wait times. (The ratio of downtime not including active repair time).
Waiting for Opportunity/Maximum Wait Time Ratio
A relative index showing the contribution of crew conflict times. This is the ratio of the time spent waiting for the crew to respond (not including crew logistic delays) to the total wait time (not including the active repair time).
Crew/Part Wait Ratio
The ratio of the crew and part delays. A value of 100% means that both waits are equal. A value greater than 100% indicates that the crew delay was in excess of the part delay. For example, a value of 200% would indicate that the wait for the crew is two times greater than the wait for the part.
Part/Crew Wait Ratio
The ratio of the part and crew delays. A value of 100% means that both waits are equal. A value greater than 100% indicates that the part delay was in excess of the crew delay. For example, a value of 200% would indicate that the wait for the part is two times greater than the wait for the crew.
Downtime Summary
Non-Waiting Time
Time that the block was undergoing active maintenance/inspection by a crew. If no crew is defined, then this will return zero.
Waiting for Opportunity
The total downtime for the block due to crew conflicts (i.e., time spent waiting for a crew while the crew is busy with another task). If no crew is defined, then this will return zero.
Waiting for Crew
The total downtime for the block due to crew wait times (i.e., time spent waiting for a crew due to logistical delay). If no crew is defined, then this will return zero.
Waiting for Parts
The total downtime for the block due to spare part wait times. If no spare part pool is defined then this will return zero.
Other Results of Interest
The remaining component (block) results are similar to those defined for the system with the exception that now they apply only to the component.
Subdiagrams and Multi Blocks in Simulation
Any subdiagrams and multi blocks that may be present in the BlockSim RBD are expanded and/or merged into a single diagram before the system is simulated. As an example, consider the system shown in the figure below.
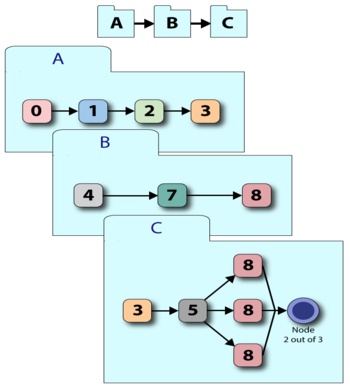
BlockSim will internally merge the system into a single diagram before the simulation, as shown in the figure below. This means that all the failure and repair properties of the items in the subdiagrams are also considered.
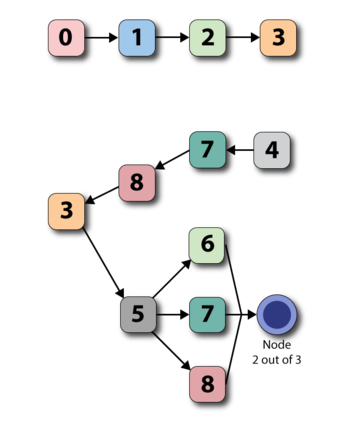
In the case of multi blocks, the blocks are also fully expanded before simulation. This means that unlike the analytical solution, the execution speed (and memory requirements) for a multi block representing ten blocks in series is identical to the representation of ten individual blocks in series.
Containers in Simulation
Standby Containers
When you simulate a diagram that contains a standby container, the container acts as the switch mechanism (as shown below) in addition to defining the standby relationships and the number of active units that are required. The container's failure and repair properties are really that of the switch itself. The switch can fail with a distribution, while waiting to switch or during the switch action. Repair properties restore the switch regardless of how the switch failed. Failure of the switch itself does not bring the container down because the switch is not really needed unless called upon to switch. The container will go down if the units within the container fail or the switch is failed when a switch action is needed. The restoration time for this is based on the repair distributions of the contained units and the switch. Furthermore, the container is down during a switch process that has a delay.
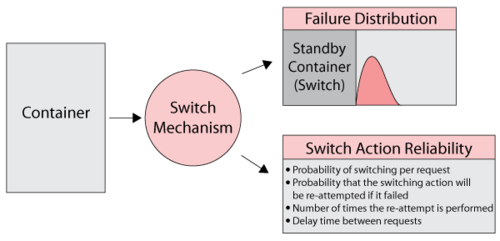
To better illustrate this, consider the following deterministic case.
- Units [math]\displaystyle{ A\,\! }[/math] and [math]\displaystyle{ B\,\! }[/math] are contained in a standby container.
- The standby container is the only item in the diagram, thus failure of the container is the same as failure of the system.
- [math]\displaystyle{ A\,\! }[/math] is the active unit and [math]\displaystyle{ B\,\! }[/math] is the standby unit.
- Unit [math]\displaystyle{ A\,\! }[/math] fails every 100 [math]\displaystyle{ tu\,\! }[/math] (active) and takes 10 [math]\displaystyle{ tu\,\! }[/math] to repair.
- [math]\displaystyle{ B\,\! }[/math] fails every 3 [math]\displaystyle{ tu\,\! }[/math] (active) and also takes 10 [math]\displaystyle{ tu\,\! }[/math] to repair.
- The units cannot fail while in quiescent (standby) mode.
- Furthermore, assume that the container (acting as the switch) fails every 30 [math]\displaystyle{ tu\,\! }[/math] while waiting to switch and takes 4 [math]\displaystyle{ tu\,\! }[/math] to repair. If not failed, the container switches with 100% probability.
- The switch action takes 7 [math]\displaystyle{ tu\,\! }[/math] to complete.
- After repair, unit [math]\displaystyle{ A\,\! }[/math] is always reactivated.
- The container does not operate through system failure and thus the components do not either.
Keep in mind that we are looking at two events on the container. The container down and container switch down.
The system event log is shown in the figure below and is as follows:
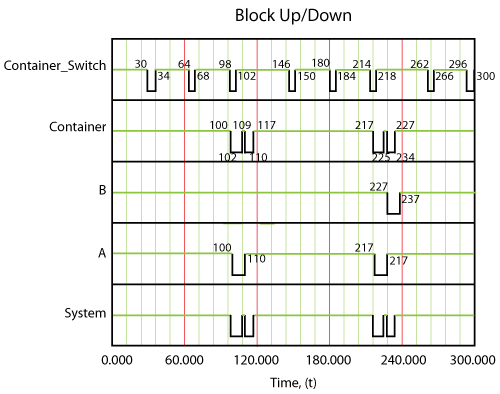
- At 30, the switch fails and gets repaired by 34. The container switch is failed and being repaired; however, the container is up during this time.
- At 64, the switch fails and gets repaired by 68. The container is up during this time.
- At 98, the switch fails. It will be repaired by 102.
- At 100, unit [math]\displaystyle{ A\,\! }[/math] fails. Unit [math]\displaystyle{ A\,\! }[/math] attempts to activate the switch to go to [math]\displaystyle{ B\,\! }[/math] ; however, the switch is failed.
- At 102, the switch is operational.
- From 102 to 109, the switch is in the process of switching from unit [math]\displaystyle{ A\,\! }[/math] to unit [math]\displaystyle{ B\,\! }[/math]. The container and system are down from 100 to 109.
- By 110, unit [math]\displaystyle{ A\,\! }[/math] is fixed and the system is switched back to [math]\displaystyle{ A\,\! }[/math] from [math]\displaystyle{ B\,\! }[/math]. The return switch action brings the container down for 7 [math]\displaystyle{ tu\,\! }[/math], from 110 to 117. During this time, note that unit [math]\displaystyle{ B\,\! }[/math] has only functioned for 1 [math]\displaystyle{ tu\,\! }[/math], 109 to 110.
- At 146, the switch fails and gets repaired by 150. The container is up during this time.
- At 180, the switch fails and gets repaired by 184. The container is up during this time.
- At 214, the switch fails and gets repaired by 218.
- At 217, unit [math]\displaystyle{ A\,\! }[/math] fails. The switch is failed at this time.
- At 218, the switch is operational and the system is switched to unit [math]\displaystyle{ B\,\! }[/math] within 7 [math]\displaystyle{ tu\,\! }[/math]. The container is down from 218 to 225.
- At 225, unit [math]\displaystyle{ B\,\! }[/math] takes over. After 2 [math]\displaystyle{ tu\,\! }[/math] of operation at 227, unit [math]\displaystyle{ B\,\! }[/math] fails. It will be restored by 237.
- At 227, unit [math]\displaystyle{ A\,\! }[/math] is repaired and the switchback action to unit [math]\displaystyle{ A\,\! }[/math] is initiated. By 234, the system is up.
- At 262, the switch fails and gets repaired by 266. The container is up during this time.
- At 296, the switch fails and gets repaired by 300. The container is up during this time.
The system results are shown in the figure below and discussed next.
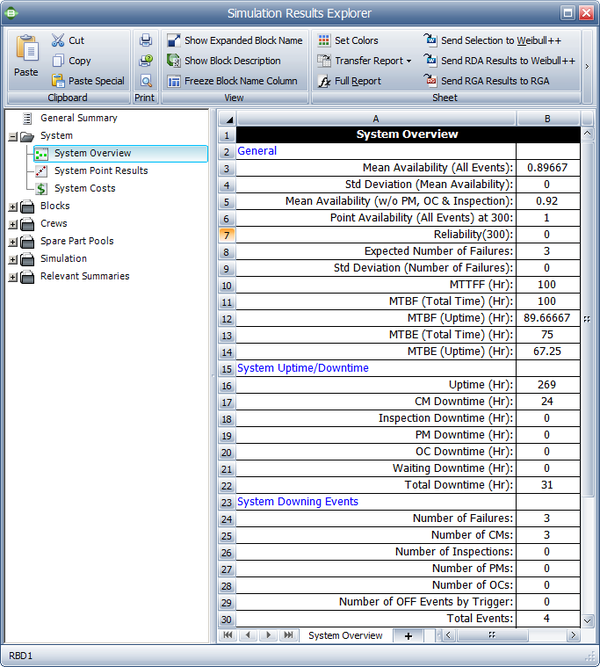
- 1. System CM Downtime is 24.
- a) CM downtime includes all downtime due to failures as well as the delay in switching from a failed active unit to a standby unit. It does not include the switchback time from the standby to the restored active unit. Thus, the times from 100 to 109, 217 to 225 and 227 to 234 are included. The time to switchback, 110 to 117, is not included.
- 2. System Total Downtime is 31.
- a) It includes the CM downtime and the switchback downtime.
- 3. Number of System Failures is 3.
- a) It includes the failures at 100, 217 and 227.
- b) This is the same as the number of CM downing events.
- 4. The Total Downing Events are 4.
- a) This includes the switchback downing event at 110.
- 5. The Mean Availability (w/o PM and Inspection) does not include the downtime due to the switchback event.
- 1. System CM Downtime is 24.
Additional Rules and Assumptions for Standby Containers
- 1) A container will only attempt to switch if there is an available non-failed item to switch to. If there is no such item, it will then switch if and when an item becomes available. The switch will cancel the action if it gets restored before an item becomes available.
- a) As an example, consider the case of unit [math]\displaystyle{ A\,\! }[/math] failing active while unit [math]\displaystyle{ B\,\! }[/math] failed in a quiescent mode. If unit [math]\displaystyle{ B\,\! }[/math] gets restored before unit [math]\displaystyle{ A\,\! }[/math], then the switch will be initiated. If unit [math]\displaystyle{ A\,\! }[/math] is restored before unit [math]\displaystyle{ B\,\! }[/math], the switch action will not occur.
- 2) In cases where not all active units are required, a switch will only occur if the failed combination causes the container to fail.
- a) For example, if [math]\displaystyle{ A\,\! }[/math], [math]\displaystyle{ B\,\! }[/math], and [math]\displaystyle{ C\,\! }[/math] are in a container for which one unit is required to be operating and [math]\displaystyle{ A\,\! }[/math] and [math]\displaystyle{ B\,\! }[/math] are active with [math]\displaystyle{ C\,\! }[/math] on standby, then the failure of either [math]\displaystyle{ A\,\! }[/math] or [math]\displaystyle{ B\,\! }[/math] will not cause a switching action. The container will switch to [math]\displaystyle{ C\,\! }[/math] only if both [math]\displaystyle{ A\,\! }[/math] and [math]\displaystyle{ B\,\! }[/math] are failed.
- 3) If the container switch is failed and a switching action is required, the switching action will occur after the switch has been restored if it is still required (i.e., if the active unit is still failed).
- 4) If a switch fails during the delay time of the switching action based on the reliability distribution (quiescent failure mode), the action is still carried out unless a failure based on the switch probability/restarts occurs when attempting to switch.
- 5) During switching events, the change from the operating to quiescent distribution (and vice versa) occurs at the end of the delay time.
- 6) The option of whether components operate while the system is down is defined at component level now (This is different from BlockSim 7, in which this option of the contained items inherit from container). Two rules here:
- a) If a path inside the container is down, blocks inside the container that are in that path do not continue to operate.
- b) Blocks that are up do not continue to operate while the container is down.
- 7) A switch can have a repair distribution and maintenance properties without having a reliability distribution.
- a) This is because maintenance actions are performed regardless of whether the switch failed while waiting to switch (reliability distribution) or during the actual switching process (fixed probability).
- 8) A switch fails during switching when the restarts are exhausted.
- 9) A restart is executed every time the switch fails to switch (based on its fixed probability of switching).
- 10) If a delay is specified, restarts happen after the delay.
- 11) If a container brings the system down, the container is responsible for the system going down (not the blocks inside the container).
- 1) A container will only attempt to switch if there is an available non-failed item to switch to. If there is no such item, it will then switch if and when an item becomes available. The switch will cancel the action if it gets restored before an item becomes available.
Load Sharing Containers
When you simulate a diagram that contains a load sharing container, the container defines the load that is shared. A load sharing container has no failure or repair distributions. The container itself is considered failed if all the blocks inside the container have failed (or [math]\displaystyle{ k\,\! }[/math] blocks in a [math]\displaystyle{ k\,\! }[/math] -out-of- [math]\displaystyle{ n\,\! }[/math] configuration).
To illustrate this, consider the following container with items [math]\displaystyle{ A\,\! }[/math] and [math]\displaystyle{ B\,\! }[/math] in a load sharing redundancy.
Assume that [math]\displaystyle{ A\,\! }[/math] fails every 100 [math]\displaystyle{ tu\,\! }[/math] and [math]\displaystyle{ B\,\! }[/math] every 120 [math]\displaystyle{ tu\,\! }[/math] if both items are operating and they fail in half that time if either is operating alone (i.e., the items age twice as fast when operating alone). They both get repaired in 5 [math]\displaystyle{ tu\,\! }[/math].
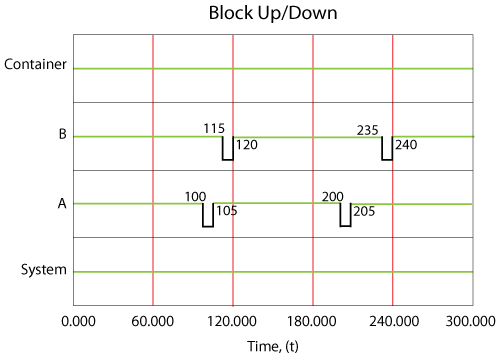
The system event log is shown in the figure above and is as follows:
- 1. At 100, [math]\displaystyle{ A\,\! }[/math] fails. It takes 5 [math]\displaystyle{ tu\,\! }[/math] to restore [math]\displaystyle{ A\,\! }[/math].
- 2. From 100 to 105, [math]\displaystyle{ B\,\! }[/math] is operating alone and is experiencing a higher load.
- 3. At 115, [math]\displaystyle{ B\,\! }[/math] fails. would normally be expected to fail at 120, however:
- a) From 0 to 100, it accumulated the equivalent of 100 [math]\displaystyle{ tu\,\! }[/math] of damage.
- b) From 100 to 105, it accumulated 10 [math]\displaystyle{ tu\,\! }[/math] of damage, which is twice the damage since it was operating alone. Put another way, [math]\displaystyle{ B\,\! }[/math] aged by 10 [math]\displaystyle{ tu\,\! }[/math] over a period of 5 [math]\displaystyle{ tu\,\! }[/math].
- c) At 105, [math]\displaystyle{ A\,\! }[/math] is restored but [math]\displaystyle{ B\,\! }[/math] has only 10 [math]\displaystyle{ tu\,\! }[/math] of life remaining at this point.
- d) [math]\displaystyle{ B\,\! }[/math] fails at 115.
- 4. At 120, [math]\displaystyle{ B\,\! }[/math] is repaired.
- 5. At 200, [math]\displaystyle{ A\,\! }[/math] fails again. [math]\displaystyle{ A\,\! }[/math] would normally be expected to fail at 205; however, the failure of [math]\displaystyle{ B\,\! }[/math] at 115 to 120 added additional damage to [math]\displaystyle{ A\,\! }[/math]. In other words, the age of [math]\displaystyle{ A\,\! }[/math] at 115 was 10; by 120 it was 20. Thus it reached an age of 100 95 [math]\displaystyle{ tu\,\! }[/math] later at 200.
- 6. [math]\displaystyle{ A\,\! }[/math] is restored by 205.
- 7. At 235, [math]\displaystyle{ B\,\! }[/math] fails. [math]\displaystyle{ B\,\! }[/math] would normally be expected to fail at 240; however, the failure of [math]\displaystyle{ A\,\! }[/math] at 200 caused the reduction.
- a) At 200, [math]\displaystyle{ B\,\! }[/math] had an age of 80.
- b) By 205, [math]\displaystyle{ B\,\! }[/math] had an age of 90.
- c) [math]\displaystyle{ B\,\! }[/math] fails 30 [math]\displaystyle{ tu\,\! }[/math] later at 235.
- 8. The system itself never failed.
Additional Rules and Assumptions for Load Sharing Containers
- 1. The option of whether components operate while the system is down is defined at component level now (This is different from BlockSim 7, in which this option of the contained items inherit from container). Two rules here:
- a) If a path inside the container is down, blocks inside the container that are in that path do not continue to operate.
- b) Blocks that are up do not continue to operate while the container is down.
- 2. If a container brings the system down, the block that brought the container down is responsible for the system going down. (This is the opposite of standby containers.)
- 1. The option of whether components operate while the system is down is defined at component level now (This is different from BlockSim 7, in which this option of the contained items inherit from container). Two rules here:
State Change Triggers
Consider a case where you have two generators, and one (A) is primary while the other (B) is standby. If A fails, you will turn B on. When A is repaired, it then becomes the standby. State change triggers (SCT) allow you to simulate this case. You can specify events that will activate and/or deactivate the block during simulation. The figure below shows the options for state change triggers in the Block Properties window.
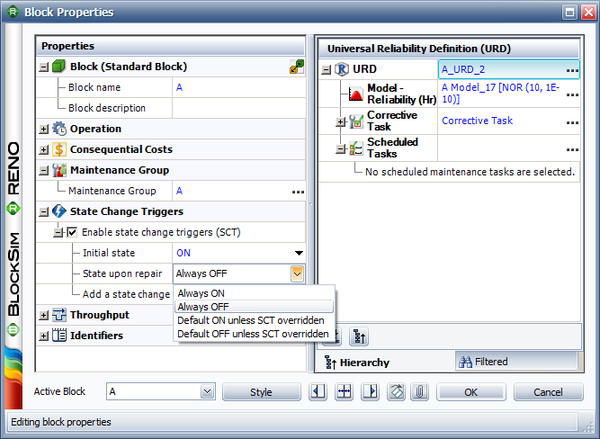
Once you have enabled state change triggers for a block, there are several options.
- Initial state allows you to specify the initial state for the block, either ON or OFF.
- State upon repair allows you to specify the state of the block after its repair. There are four choices: Always ON, Always OFF, Default ON unless SCT Overridden and Default OFF unless SCT Overridden. In the Assumptions sections, we will explain what these choices mean and illustrate them using an example.
- Add a state change trigger allows you to add a state change trigger to the block.
The state change trigger can either activate or deactivate the block when items in specified maintenance groups go down or are restored. To define the state change trigger, specify the triggering event (i.e., an item goes down or an item is restored), the state change (i.e., the block is activated or deactivated) and the maintenance group(s) in which the triggering event must happen in order to trigger the state change. Note that the current block does not need to be part of the specified maintenance group(s) to use this functionality.
The State Change Trigger window is shown in the figure below:
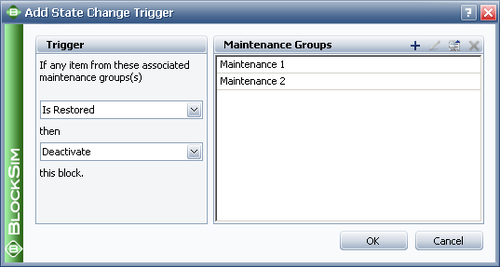
Assumptions
- A block cannot trigger events on itself. For example, if Block 1 is the only block that belongs to MG 1 and Block 1 is set to be turned ON or OFF based on MG 1, this trigger is ignored.
- OFF events cannot trigger other events. This means that things cannot be turned OFF in cascade. For example, if Block 1 going down turns OFF Block 2 and Block 2 going down turns OFF Block 3, a failure by Block 1 will not turn OFF Block 3. Block 3 would have to be directly associated with downing events of Block 1 for this to happen. The reason for this restriction is that allowing OFF events to trigger other events can cause circular reference problems. For example, four blocks A, B, C and D are in parallel. Block A belongs to MG A and initially it is ON. Block B belongs to MG B and its initial status is also ON. Block C belongs to MG C and its initial status is OFF. Block D belongs to MG D and its initial status is ON. A failure of Block A will turn OFF Block B. Then Block B will turn Block C ON and finally C will turn OFF Block D. However, if an OFF event for Block D will turn Block B ON, and an ON event for Block B will turn Block C OFF, and an OFF event for Block C will turn Block D ON, then there is a circular reference problem.
- Upon restoration states:
- Always ON: Upon restoration, the block will always be on.
- Always OFF: Upon restoration, the block will always be off.
- Default ON unless SCT overridden: Upon restoration, the block will be on unless a request is made to turn this block off while the block is down and the request is still applicable at the time of restoration. For example, assume Block A's state upon repair is ON unless SCT overridden. If a failure of Block B triggers a request to turn Block A off but Block A is down, when the maintenance for Block A is completed, Block A will be turned off if Block B is still down.
- Default off unless SCT overridden: Upon restoration, the block will be off unless a request is made to turn this block on while the block is down and the request is still applicable at the time of restoration
- Maintenance while block is off: Maintenance tasks will be performed. At the end of the maintenance, "upon restoration" rules will be checked to determine the state of the block.
- Assumptions for phases: In Versions 10 and earlier, the state of a block (on/off) was determined at the beginning of each phase based on the "Initial state" setting of the block for that phase. Starting in Version 11, the state of the block transfers across phases instead of resetting based on initial settings.
- If there are multiple triggering requests put on a block when it is down, only the latest one is considered. The latest request will cancel all requests before it. For example, Block A fails at 20 and is down until 70. Block B fails at 30 and Block C fails at 40. Block A has state change triggers enabled such that it will be activated when Block B fails and it will be deactivated when Block C fails. Thus from 20 to 70, at 30, Block B will put a request on Block A to turn it ON and at 40, Block C will put another request to turn it OFF. In this case, according to our assumption, the request from Block C at 40 will cancel the request from Block B at 30. In the end, only the request from Block C will be considered. Thus, Block A will be turned OFF at 70 when it is done with repair.
Example: Using SCT for Standby Rotation
This example illustrates the use of state change triggers in BlockSim (Version 8 and above) by using a simple standby configuration. Note that this example could also be done using the standby container functionality in BlockSim.
More specifically, the following settings are illustrated:
- State Upon Repair: Default OFF unless SCT overridden
- Activate a block if any item from these associated maintenance group(s) goes down
Problem Statement
Assume three devices A, B and C in a standby redundancy (or only one unit is needed for system operation). The system begins with device A working. When device A fails, B is turned on and repair actions are initiated on A. When B fails, C is turned on and so forth.
BlockSim Solution
The BlockSim model of this system is shown in the figure below.
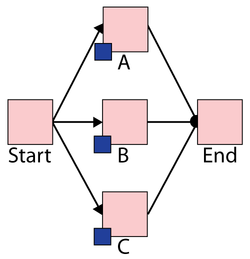
- The failure distributions of all three blocks follow a Weibull distribution with Beta = 1.5 and Eta = 1,000 hours.
- The repair distributions of the three blocks follow a Weibull distribution with Beta = 1.5 and Eta = 100 hours.
- After repair, the blocks are "as good as new."
There are three maintenance groups, 2_A, 2_B and 2_C, set as follows:
- Block A belongs to maintenance group 2_A.
- It has a state change trigger.
- The initial state is ON and the state upon repair is "Default OFF unless SCT overridden."
- If any item from maintenance group 2_C goes down, then activate this block.
- It has a state change trigger.
- Block B belongs to maintenance group 2_B.
- It has a state change trigger.
- The initial state is OFF and the state upon repair is "Default OFF unless SCT overridden."
- If any item from maintenance group 2_A goes down, then activate this block.
- It has a state change trigger.
- Block C belongs to maintenance group 2_C.
- It has a state change trigger.
- The initial state is OFF and the state upon repair is "Default OFF unless SCT overridden."
- If any item from maintenance group 2_B goes down, then activate this block.
- It has a state change trigger.
- All blocks A, B and C are as good as new after repair.
System Events
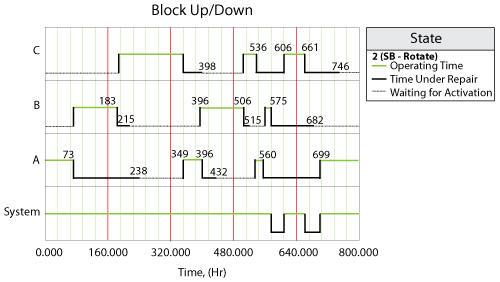
The system event log for a single run through the simulation algorithm is shown in the Block Up/Down plot below, and is as follows:
- At 73 hours, Block A fails and activates Block B.
- At 183 hours, Block B fails and activates Block C.
- At 215 hours, Block B is done with repair. At this time, Block C is operating, so according to the settings, Block B is standby.
- At 238 hours, Block A is done with repair. At this time, Block C is operating. Thus Block A is standby.
- At 349 hours, Block C fails and activates Block A.
- At 396 hours, Block A fails and activates Block B.
- At 398 hours, Block C is done with repair. At this time, Block B is operating. Thus Block C is standby.
- At 432 hours, Block A is done with repair. At this time, Block B is operating. Thus Block A is standby.
- At 506 hours, Block B fails and activates Block C.
- At 515 hours, Block B is done with repair and stays standby because Block C is operating.
- At 536 hours, Block C fails and activates Block A.
- At 560 hours, Block A fails and activates Block B.
- At 575 hours, Block B fails and makes a request to activate Block C. However, Block C is under repair at the time. Thus when Block C is done with repair at 606 hours, the OFF setting is overridden and it is operating immediately.
- At 661 hours, Block C fails and makes a request to activate Block A. However, Block A is under repair at the time. Thus when Block A is done with repair at 699 hours, the OFF setting is overridden and it is operating immediately.
- Block B and Block C are done with repair at 682 hours and at 746 hours respectively. However, at these two time points, Block A is operating. Thus they are both standby upon repair according to the settings.
Discussion
Even though the examples and explanations presented here are deterministic, the sequence of events and logic used to view the system is the same as the one that would be used during simulation. The difference is that the process would be repeated multiple times during simulation and the results presented would be the average results over the multiple runs.
Additionally, multiple metrics and results are presented and defined in this chapter. Many of these results can also be used to obtain additional metrics not explicitly given in BlockSim's Simulation Results Explorer. As an example, to compute mean availability with inspections but without PMs, the explicit downtimes given for each event could be used. Furthermore, all of the results given are for operating times starting at zero to a specified end time (although the components themselves could have been defined with a non-zero starting age). Results for a starting time other than zero could be obtained by running two simulations and looking at the difference in the detailed results where applicable. As an example, the difference in uptimes and downtimes can be used to determine availabilities for a specific time window.
