|
|
| (28 intermediate revisions by 5 users not shown) |
| Line 1: |
Line 1: |
| {| class="FCK__ShowTableBorders" border="0" cellspacing="0" cellpadding="0" align="center"; style="width:100%;" | | <noinclude>{{Banner Weibull Examples}}{{Navigation box}} |
| |-
| | ''These examples appear in the [[The_Normal_Distribution|Life Data Analysis Reference book]].'' |
| | valign="middle" align="left" bgcolor=EEEDF7|[[Image:Weibull-Examples-banner.png|400px|center]]
| | </noinclude> |
| |}
| | The following examples illustrate the different types of life data that can be analyzed in Weibull++ using the normal distribution. For more information on the different types of life data, see [[Life Data Classification]]. |
|
| |
|
| Fourteen units were reliability tested and the following life test data were obtained:
| |
|
| |
|
| | ===Complete Data Example=== |
| | 6 units are tested to failure. The following failure times data are obtained: 12125, 11260, 12080, 12825, 13550 and 14670 hours. Assuming that the data are normally distributed, do the following: |
|
| |
|
| {|align="center" border=1 cellspacing=1
| |
| |-
| |
| |colspan="2" style="text-align:center"|Table 8.1 -The test data for Example 2
| |
| |-
| |
| !Data point index
| |
| !Time-to-failure
| |
| |-
| |
| |1 ||5
| |
| |-
| |
| |2 ||10
| |
| |-
| |
| |3 ||15
| |
| |-
| |
| |4 ||20
| |
| |-
| |
| |5 ||25
| |
| |-
| |
| |6 ||30
| |
| |-
| |
| |7||35
| |
| |-
| |
| |8||40
| |
| |-
| |
| |9||50
| |
| |-
| |
| |10||60
| |
| |-
| |
| |11||70
| |
| |-
| |
| |12||80
| |
| |-
| |
| |13||90
| |
| |-
| |
| |14||100
| |
| |}
| |
|
| |
|
| | '''Objectives''' |
|
| |
|
| Assuming the data follow a normal distribution, estimate the parameters and determine the correlation coefficient, <math>\rho </math> , using rank regression on Y.
| | :1. Find the parameters for the data set, using the Rank Regression on X (RRX) parameter estimation method |
| | :2. Obtain the probability plot for the data with 90%, two-sided Type 1 confidence bounds. |
| | :3. Obtain the ''pdf'' plot for the data. |
| | :4. Using the Quick Calculation Pad (QCP), determine the reliability for a mission of 11,000 hours, as well as the upper and lower two-sided 90% confidence limit on this reliability. |
| | :5. Using the QCP, determine the MTTF, as well as the upper and lower two-sided 90% confidence limit on this MTTF. |
| | :6. Obtain tabulated values for the failure rate for 10 different mission end times. The mission end times are 1,000 to 10,000 hours, using increments of 1,000 hours. |
|
| |
|
| ====Solution====
| |
| Construct a table like the one shown next.
| |
|
| |
|
| <center><math>\overset{{}}{\mathop{\text{Table 8}\text{.2 - Least Squares Analysis}}}\,</math></center>
| | '''Solution''' |
|
| |
| <center><math>\begin{matrix}
| |
| \text{N} & \text{T}_{i} & \text{F(T}_{i}\text{)} & \text{y}_{i} & \text{T}_{i}^{2} & \text{y}_{i}^{2} & \text{T}_{i}\text{ y}_{i} \\
| |
| \text{1} & \text{5} & \text{0}\text{.0483} & \text{-1}\text{.6619} & \text{25} & \text{2}\text{.7619} & \text{-8}\text{.3095} \\
| |
| \text{2} & \text{10} & \text{0}\text{.1170} & \text{-1}\text{.1901} & \text{100} & \text{1}\text{.4163} & \text{-11}\text{.9010} \\
| |
| \text{3} & \text{15} & \text{0}\text{.1865} & \text{-0}\text{.8908} & \text{225} & \text{0}\text{.7935} & \text{-13}\text{.3620} \\
| |
| \text{4} & \text{20} & \text{0}\text{.2561} & \text{-0}\text{.6552} & \text{400} & \text{0}\text{.4292} & \text{-13}\text{.1030} \\
| |
| \text{5} & \text{25} & \text{0}\text{.3258} & \text{-0}\text{.4512} & \text{625} & \text{0}\text{.2036} & \text{-11}\text{.2800} \\
| |
| \text{6} & \text{30} & \text{0}\text{.3954} & \text{-0}\text{.2647} & \text{900} & \text{0}\text{.0701} & \text{-7}\text{.9422} \\
| |
| \text{7} & \text{35} & \text{0}\text{.4651} & \text{-0}\text{.0873} & \text{1225} & \text{0}\text{.0076} & \text{-3}\text{.0542} \\
| |
| \text{8} & \text{40} & \text{0}\text{.5349} & \text{0}\text{.0873} & \text{1600} & \text{0}\text{.0076} & \text{3}\text{.4905} \\
| |
| \text{9} & \text{50} & \text{0}\text{.6046} & \text{0}\text{.2647} & \text{2500} & \text{0}\text{.0701} & \text{13}\text{.2370} \\
| |
| \text{10} & \text{60} & \text{0}\text{.6742} & \text{0}\text{.4512} & \text{3600} & \text{0}\text{.2036} & \text{27}\text{.0720} \\
| |
| \text{11} & \text{70} & \text{0}\text{.7439} & \text{0}\text{.6552} & \text{4900} & \text{0}\text{.4292} & \text{45}\text{.8605} \\
| |
| \text{12} & \text{80} & \text{0}\text{.8135} & \text{0}\text{.8908} & \text{6400} & \text{0}\text{.7935} & \text{71}\text{.2640} \\
| |
| \text{13} & \text{90} & \text{0}\text{.8830} & \text{1}\text{.1901} & \text{8100} & \text{1}\text{.4163} & \text{107}\text{.1090} \\
| |
| \text{14} & \text{100} & \text{0}\text{.9517} & \text{1}\text{.6619} & \text{10000} & \text{2}\text{.7619} & \text{166}\text{.1900} \\
| |
| \mathop{}_{}^{} & \text{630} & {} & \text{0} & \text{40600} & \text{11}\text{.3646} & \text{365}\text{.2711} \\
| |
| \end{matrix}</math></center>
| |
|
| |
|
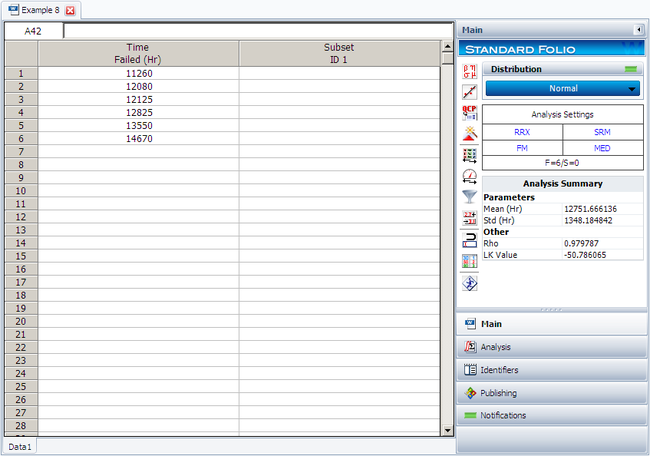
| | The following figure shows the data as entered in Weibull++, as well as the calculated parameters. |
|
| |
|
| :• The median rank values ( <math>F({{T}_{i}})</math> ) can be found in rank tables, available in many statistical texts, or they can be estimated by using the Quick Statistical Reference in Weibull++.
| |
| :• The <math>{{y}_{i}}</math> values were obtained from standardized normal distribution's area tables by entering for <math>F(z)</math> and getting the corresponding <math>z</math> value ( <math>{{y}_{i}}</math> ). As with the median rank values, these standard normal values can be obtained with the Quick Statistical Reference.
| |
| Given the values in Table 8.2, calculate <math>\widehat{a}</math> and <math>\widehat{b}</math> using Eqns. (aan) and (bbn):
| |
|
| |
|
| ::<math>\begin{align} | | [[Image:Normal Distribution Example 8 Data.png|center|650px| ]] |
| & \widehat{b}= & \frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{T}_{i}}{{y}_{i}}-(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{T}_{i}})(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}})/14}{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,T_{i}^{2}-{{(\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{T}_{i}})}^{2}}/14} \\
| |
| & & \\
| |
| & \widehat{b}= & \frac{365.2711-(630)(0)/14}{40,600-{{(630)}^{2}}/14}=0.02982
| |
| \end{align}</math>
| |
|
| |
|
| :and:
| |
|
| |
|
| ::<math>\widehat{a}=\overline{y}-\widehat{b}\overline{T}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\widehat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{T}_{i}}}{N}</math>
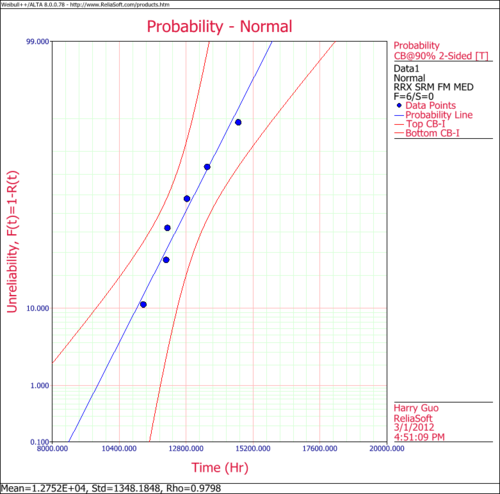
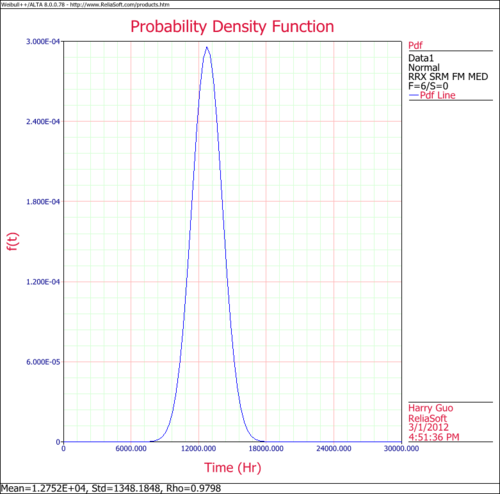
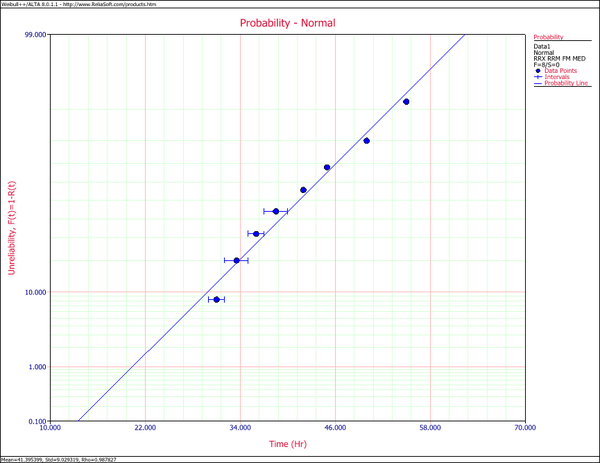
| | The following figures show the probability plot with the 90% two-sided confidence bounds and the ''pdf'' plot. |
|
| |
|
| :or:
| |
|
| |
|
| ::<math>\widehat{a}=\frac{0}{14}-(0.02982)\frac{630}{14}=-1.3419</math> | | [[Image:Normal Distribution Example 8 Probability Plot.png|center|500px|Probability Plot ]] |
|
| |
|
| Therefore, from Eqn. (bn):
| |
|
| |
|
| ::<math>\widehat{\sigma}=\frac{1}{\hat{b}}=\frac{1}{0.02982}=33.5367</math> | | [[Image:Normal Distribution Example 8 pdf Plot.png|center|500px|PDF Plot ]] |
|
| |
|
| :and from Eqn. (an):
| |
|
| |
|
| ::<math>\widehat{\mu }=-\widehat{a}\cdot \widehat{\sigma }=-(-1.3419)\cdot 33.5367\simeq 45</math>
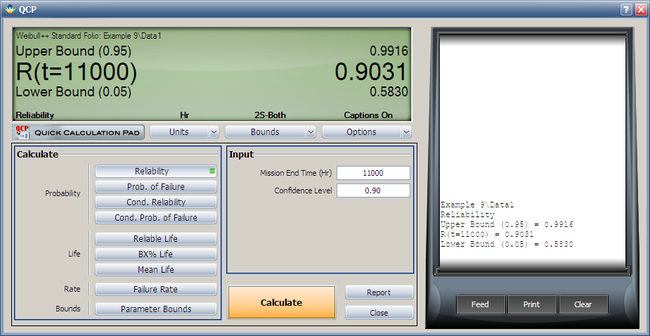
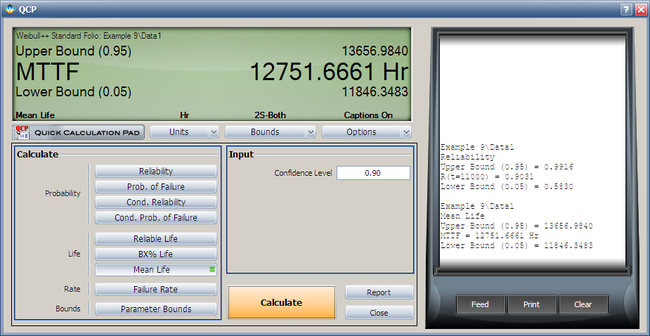
| | Both the reliability and MTTF can be easily obtained from the QCP. The QCP, with results, for both cases is shown in the next two figures. |
|
| |
|
| or <math>\widehat{\mu }=45</math> hours <math>.</math>
| |
|
| |
|
| The correlation coefficient can be estimated using Eqn. (RHOn):
| | [[Image:Normal Distribution Example 9 QCP 1.png|center|650px| ]] |
|
| |
|
| ::<math>\widehat{\rho }=0.979</math>
| |
|
| |
|
| The preceding example can be repeated using Weibull++ .
| | [[Image:Normal Distribution Example 9 QCP 2.png|center|650px| ]] |
|
| |
|
| :• Create a new folio for Times-to-Failure data, and enter the data given in Table 8.1.
| |
| :• Choose Normal from the Distributions list.
| |
| :• Go to the Analysis page and select Rank Regression on Y (RRY).
| |
| :• Click the Calculate icon located on the Main page.
| |
|
| |
|
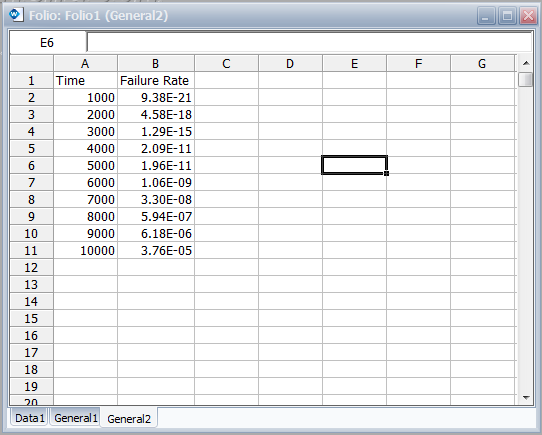
| [[Image:weibullfolio1.png|thumb|center|400px| ]] | | To obtain tabulated values for the failure rate, use the Analysis Workbook or General Spreadsheet features that are included in Weibull++. (For more information on these features, please refer to the Weibull++ User's Guide. For a step-by-step example on creating Weibull++ reports, please see the [http://www.reliasoft.tv/weibull/startguide/weibull_qsg_2.html Quick Start Guide]). The following worksheet shows the mission times and the corresponding failure rates. |
|
| |
|
| The probability plot is shown next.
| |
|
| |
|
| [[Image:weibullfolioplot1st.png|thumb|center|400px| ]] | | [[Image:folio^E.png|center|550px]] |
| ===Weibull Normal Distribution Example===
| |
| Using the data of Example 2 and assuming a normal distribution, estimate the parameters and determine the correlation coefficient, <math>\rho </math> , using rank regression on X.
| |
|
| |
|
| ====Solution==== | | ===Suspension Data Example=== |
| Table 8.2 constructed in Example 2 applies to this example also. Using the values on this table, we get:
| | 19 units are being reliability tested and the following is a table of their times-to-failure and suspensions. |
|
| |
|
| ::<math>\begin{align}
| | {|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" |
| \hat{b}= & \frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{T}_{i}}{{y}_{i}}-\tfrac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{T}_{i}}\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}}}{14}}{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,y_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}} \right)}^{2}}}{14}} \\
| | |- |
| \widehat{b}= & \frac{365.2711-(630)(0)/14}{11.3646-{{(0)}^{2}}/14}=32.1411
| | |colspan="3" style="text-align:center"| '''Non-Grouped Data Times-to-Failure Data with Suspensions''' |
| \end{align}</math>
| | |- |
| | | !Data point index |
| :and:
| | !Last Inspected |
| | | !State End Time |
| ::<math>\hat{a}=\overline{x}-\hat{b}\overline{y}=\frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{T}_{i}}}{14}-\widehat{b}\frac{\underset{i=1}{\overset{14}{\mathop{\sum }}}\,{{y}_{i}}}{14}</math>
| | |- |
| | | |1 ||F||2 |
| :or:
| | |- |
| | | |2 ||S||3 |
| ::<math>\widehat{a}=\frac{630}{14}-(32.1411)\frac{(0)}{14}=45</math>
| | |- |
| | | |3 ||F||5 |
| Therefore, from Eqn. (bnx):
| | |- |
| | | |4 ||S||7 |
| ::<math>\widehat{\sigma }=\widehat{b}=32.1411</math>
| | |- |
| | | |5 ||F||11 |
| :and from Eqn. (anx):
| | |- |
| | | |6 ||S||13 |
| ::<math>\widehat{\mu }=\widehat{a}=45\text{ hours}</math>
| | |- |
| | | |7||S||17 |
| The correlation coefficient is found using Eqn. (RHOn):
| | |- |
| | | |8||S||19 |
| ::<math>\widehat{\rho }=0.979</math>
| | |- |
| | | |9 ||F||23 |
| Note that the results for regression on X are not necessarily the same as the results for regression on Y. The only time when the two regressions are the same (i.e. will yield the same equation for a line) is when the data lie perfectly on a straight line.
| | |- |
| Using Weibull++ , Rank Regression on X (RRX) can be selected from the Analysis page.
| | |10 ||F||29 |
| | | |- |
| [[Image:weibullfolio1.png|thumb|center|400px| ]]
| | |11 ||S||31 |
| | | |- |
| The plot of the solution for this example is shown next.
| | |12 ||F||37 |
| | | |- |
| [[Image:weibullfolioplot1.png|thumb|center|400px| ]]
| | |13 ||S||41 |
| <math></math>
| | |- |
| | |14 ||F||43 |
| | |- |
| | |15||S||47 |
| | |- |
| | |16||S||53 |
| | |- |
| | |17||F||59 |
| | |- |
| | |18||S||61 |
| | |- |
| | |19||S||67 |
| | |} |
|
| |
|
| ====Weibull Normal Distribution Example====
| |
| Using the data of Example 2 and assuming a normal distribution, estimate the parameters using the MLE method.
| |
|
| |
| =====Solution=====
| |
| In this example we have non-grouped data without suspensions and without interval data. The partial derivatives of the normal log-likelihood function, <math>\Lambda ,</math> are given by:
| |
|
| |
|
| | Using the normal distribution and the maximum likelihood (MLE) parameter estimation method, the computed parameters are: |
|
| |
|
| ::<math>\begin{align} | | ::<math>\begin{align} |
| \frac{\partial \Lambda }{\partial \mu }= & \frac{1}{{{\sigma }^{2}}}\underset{i=1}{\overset{14}{\mathop \sum }}\,({{T}_{i}}-\mu )=0 \\
| | & \widehat{\mu }= & 48.07 \\ |
| \frac{\partial \Lambda }{\partial \sigma }= & \underset{i=1}{\overset{14}{\mathop \sum }}\,\left( \frac{{{T}_{i}}-\mu }{{{\sigma }^{3}}}-\frac{1}{\sigma } \right)=0
| | & {{{\hat{\sigma }}}_{T}}= & 28.41. |
| \end{align}</math> | | \end{align}\,\!</math> |
|
| |
|
|
| |
|
| (The derivations of these equations are presented in Appendix C.) Substituting the values of <math>{{T}_{i}}</math> and solving the above system simultaneously, we get <math>\widehat{\sigma }=29.58</math> hours <math>,</math> <math>\widehat{\mu }=45</math> hours <math>.</math>
| | If we analyze the data set with the rank regression on x (RRX) method, the computed parameters are: |
| | |
| The Fisher matrix is:
| |
| | |
| ::<math>\left[ \begin{matrix}
| |
| \widehat{Var}\left( \widehat{\mu } \right)=62.5000 & {} & \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right)=0.0000 \\
| |
| {} & {} & {} \\
| |
| \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right)=0.0000 & {} & \widehat{Var}\left( \widehat{\sigma } \right)=31.2500 \\
| |
| \end{matrix} \right]</math>
| |
| | |
|
| |
| Using Weibull++ , the MLE method can be selected from the Set Analysis page.
| |
| | |
| [[Image:weibullfolio1.png|thumb|center|400px| ]]
| |
| | |
| The plot of the solution for this example is shown next.
| |
| | |
| [[Image:weibullfolioplot1.png|thumb|center|400px| ]]
| |
| ====Weibull Normal Distribution Example====
| |
| Five units are put on a reliability test and experience failures at 12, 24, 28, 34, and 46 hours. Assuming a normal distribution, the MLE parameter estimates are calculated to be <math>\widehat{\mu }=28.8</math> and <math>\widehat{\sigma }=11.2143.</math> Calculate the two-sided 80% confidence bounds on these parameters using the likelihood ratio method.
| |
| =====Solution=====
| |
| The first step is to calculate the likelihood function for the parameter estimates:
| |
|
| |
|
| ::<math>\begin{align} | | ::<math>\begin{align} |
| L(\widehat{\mu },\widehat{\sigma })= & \underset{i=1}{\overset{N}{\mathop \prod }}\,f({{x}_{i}};\widehat{\mu },\widehat{\sigma })=\underset{i=1}{\overset{5}{\mathop \prod }}\,\frac{1}{\widehat{\sigma }\cdot \sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( \tfrac{{{x}_{i}}-\widehat{\mu }}{\widehat{\sigma }} \right)}^{2}}}} \\
| | & \widehat{\mu }= & 46.40 \\ |
| L(\widehat{\mu },\widehat{\sigma })= & \underset{i=1}{\overset{5}{\mathop \prod }}\,\frac{1}{11.2143\cdot \sqrt{2\pi }}\cdot {{e}^{-\tfrac{1}{2}{{\left( \tfrac{{{x}_{i}}-28.8}{11.2143} \right)}^{2}}}} \\
| | & {{{\hat{\sigma }}}_{T}}= & 28.64. |
| L(\widehat{\mu },\widehat{\sigma })= & 4.676897\times {{10}^{-9}}
| | \end{align}\,\!</math> |
| \end{align}</math> | |
|
| |
|
| where <math>{{x}_{i}}</math> are the original time-to-failure data points. We can now rearrange Eqn. (lratio3) to the form:
| |
|
| |
|
| ::<math>L(\mu ,\sigma )-L(\widehat{\mu },\widehat{\sigma })\cdot {{e}^{\tfrac{-\chi _{\alpha ;1}^{2}}{2}}}=0</math>
| | For the rank regression on y (RRY) method, the parameters are: |
| | |
| | |
| Since our specified confidence level, <math>\delta </math> , is 80%, we can calculate the value of the chi-squared statistic, <math>\chi _{0.8;1}^{2}=1.642374.</math> We can now substitute this information into the equation:
| |
|
| |
|
| ::<math>\begin{align} | | ::<math>\begin{align} |
| L(\mu ,\sigma )-L(\widehat{\mu },\widehat{\sigma })\cdot {{e}^{\tfrac{-\chi _{\alpha ;1}^{2}}{2}}}= & 0, \\
| | & \widehat{\mu }= & 47.34 \\ |
| \\ | | & {{{\hat{\sigma }}}_{T}}= & 29.96. |
| L(\mu ,\sigma )-4.676897\times {{10}^{-9}}\cdot {{e}^{\tfrac{-1.642374}{2}}}= & 0, \\
| | \end{align}\,\!</math> |
| \\
| |
| L(\mu ,\sigma )-2.057410\times {{10}^{-9}}= & 0.
| |
| \end{align}</math> | |
| | |
| | |
| It now remains to find the values of <math>\mu </math> and <math>\sigma </math> which satisfy this equation. This is an iterative process that requires setting the value of <math>\mu </math> and finding the appropriate values of <math>\sigma </math> , and vice versa.
| |
| | |
| The following table gives the values of <math>\sigma </math> based on given values of <math>\mu </math> .
| |
|
| |
|
| [[Image:tableofmu.gif|thumb|center|400px| ]]
| |
|
| |
|
| <math></math>
| | ===Interval Censored Data Example=== |
| [[Image:circleplot.gif|thumb|center|400px| ]]
| | 8 units are being reliability tested, and the following is a table of their failure times: |
|
| |
|
| | | {|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" |
| <center><math>\begin{matrix}
| |
| \text{ }\!\!\mu\!\!\text{ } & {{\text{ }\!\!\sigma\!\!\text{ }}_{\text{1}}} & {{\text{ }\!\!\sigma\!\!\text{ }}_{\text{2}}} & \text{ }\!\!\mu\!\!\text{ } & {{\text{ }\!\!\sigma\!\!\text{ }}_{\text{1}}} & {{\text{ }\!\!\sigma\!\!\text{ }}_{\text{2}}} \\
| |
| \text{22}\text{.0} & \text{12}\text{.045} & \text{14}\text{.354} & \text{29}\text{.0} & \text{7.849}& \text{19.909} \\
| |
| \text{22}\text{.5} & \text{11}\text{.004} & \text{15}\text{.310} & \text{29}\text{.5} & \text{7}\text{.876} & \text{17}\text{.889} \\
| |
| \text{23}\text{.0} & \text{10}\text{.341} & \text{15}\text{.894} & \text{30}\text{.0} & \text{7}\text{.935} & \text{17}\text{.844} \\
| |
| \text{23}\text{.5} & \text{9}\text{.832} & \text{16}\text{.328} & \text{30}\text{.5} & \text{8}\text{.025} & \text{17}\text{.776} \\
| |
| \text{24}\text{.0} & \text{9}\text{.418} & \text{16}\text{.673} & \text{31}\text{.0} & \text{8}\text{.147} & \text{17}\text{.683} \\
| |
| \text{24}\text{.5} & \text{9}\text{.074} & \text{16}\text{.954} & \text{31}\text{.5} & \text{8}\text{.304} & \text{17}\text{.562} \\
| |
| \text{25}\text{.0} & \text{8}\text{.784} & \text{17}\text{.186} & \text{32}\text{.0} & \text{8}\text{.498} & \text{17}\text{.411} \\
| |
| \text{25}\text{.5} & \text{8}\text{.542} & \text{17}\text{.377} & \text{32}\text{.5} & \text{8}\text{.732} & \text{17}\text{.227} \\
| |
| \text{26}\text{.0} & \text{8}\text{.340} & \text{17}\text{.534} & \text{33}\text{.0} & \text{9}\text{.012} & \text{17}\text{.004} \\
| |
| \text{26}\text{.5} & \text{8}\text{.176} & \text{17}\text{.661} & \text{33}\text{.5} & \text{9}\text{.344} & \text{16}\text{.734} \\
| |
| \text{27}\text{.0} & \text{8}\text{.047} & \text{17}\text{.760} & \text{34}\text{.0} & \text{9}\text{.742} & \text{16}\text{.403} \\
| |
| \text{27}\text{.5} & \text{7}\text{.950} & \text{17}\text{.833} & \text{34}\text{.5} & \text{10}\text{.229} & \text{15}\text{.990} \\
| |
| \text{28}\text{.0} & \text{7}\text{.885} & \text{17}\text{.882} & \text{35}\text{.0} & \text{10}\text{.854} & \text{15}\text{.444} \\
| |
| \text{28}\text{.5} & \text{7}\text{.852} & \text{17}\text{.907} & \text{35}\text{.5} & \text{11}\text{.772} & \text{14}\text{.609} \\
| |
| \end{matrix}</math></center>
| |
| | |
| This data set is represented graphically in the following contour plot:
| |
| | |
| (Note that this plot is generated with degrees of freedom <math>k=1</math> , as we are only determining bounds on one parameter. The contour plots generated in Weibull++ are done with degrees of freedom <math>k=2</math> , for use in comparing both parameters simultaneously.) As can be determined from the table, the lowest calculated value for <math>\sigma </math> is 7.849, while the highest is 17.909. These represent the two-sided 80% confidence limits on this parameter. Since solutions for the equation do not exist for values of <math>\mu </math> below 22 or above 35.5, these can be considered the two-sided 80% confidence limits for this parameter. In order to obtain more accurate values for the confidence limits on <math>\mu </math> , we can perform the same procedure as before, but finding the two values of <math>\mu </math> that correspond with a given value of <math>\sigma .</math> Using this method, we find that the two-sided 80% confidence limits on <math>\mu </math> are 21.807 and 35.793, which are close to the initial estimates of 22 and 35.5.
| |
| ====Weibull Normal Distribution Example====
| |
| For the data given in Example 5, determine the two-sided 80% confidence bounds on the time estimate for a reliability of 40%. The ML estimate for the time at <math>R(t)=40%</math> is 31.637.
| |
| =====Solution=====
| |
| In this example, we are trying to determine the two-sided 80% confidence bounds on the time estimate of 31.637. This is accomplished by substituting <math>R=0.40</math> and <math>\alpha =0.8</math> into Eqn. (normliketr), and varying <math>\sigma </math> until the maximum and minimum values of <math>t</math> are found. The following table gives the values of <math>t</math> based on given values of <math>\sigma </math> .
| |
| | |
| [[Image:tabletbasedonsigma.gif|thumb|center|400px| ]]
| |
| <math></math>
| |
| | |
| This data set is represented graphically in the following contour plot:
| |
| | |
| [[Image:ovalplot.gif|thumb|center|400px| ]]
| |
| | |
| | |
| As can be determined from the table, the lowest calculated value for <math>t</math> is 25.046, while the highest is 39.250. These represent the 80% confidence limits on the time at which reliability is equal to 40%.
| |
| ====Weibull Normal Distribution Example==== | |
| For the data given in Example 5, determine the two-sided 80% confidence bounds on the reliability estimate for <math>t=30</math> . The ML estimate for the reliability at <math>t=30</math> is 45.739%.
| |
| | |
| =====Solution=====
| |
| In this example, we are trying to determine the two-sided 80% confidence bounds on the reliability estimate of 45.739%. This is accomplished by substituting <math>t=30</math> and <math>\alpha =0.8</math> into Eqn. (normliketr), and varying <math>\sigma </math> until the maximum and minimum values of <math>R</math> are found. The following table gives the values of <math>R</math> based on given values of <math>\sigma </math> .
| |
| | |
| [[Image:tablerbasedonsigma.gif|thumb|center|400px| ]]
| |
| | |
| This data set is represented graphically in the following contour plot:
| |
| | |
| [[Image:crazyoplot.gif|thumb|center|400px| ]]
| |
| | |
| | |
| As can be determined from the table, the lowest calculated value for <math>R</math> is 24.776%, while the highest is 68.000%. These represent the 80% two-sided confidence limits on the reliability at <math>t=30</math> .
| |
| | |
| ==General Examples==
| |
| === Weibull Normal Distribution Example===
| |
| Six units are tested to failure with the following hours-to-failure data obtained: 12125, 11260, 12080, 12825, 13550 and 14670 hours. Assuming the data are normally distributed, do the following:
| |
| 8-1. Find the parameters for the data. (Use Rank Regression on X to duplicate the results shown in this example.)
| |
| 8-2. Obtain the probability plot for the data with 90%, two-sided Type 1 confidence bounds.
| |
| 8-3. Obtain the <math>pdf</math> plot for these data.
| |
| | |
| ====Solutions====
| |
| 8-1. The next figure shows the data as entered in Weibull++, as well as the calculated parameters.
| |
| | |
| <math></math>
| |
| [[Image:11260folio.png|thumb|center|400px| ]]
| |
| | |
| | |
| 8-2. Obtain the probability plot as before. To plot confidence bounds, from the Plot Options menu choose Confidence Bounds and then Show Confidence Bounds. On the Type and Settings page of the Confidence Bounds window, select Two Sided Bounds, make sure Type 1 is selected, and then enter 90 in the Confidence level, % box, and click OK, as shown next.
| |
| | |
| <math></math>
| |
| [[Image:11260CBS.png|thumb|center|400px| ]]
| |
| | |
| | |
| The following plot should appear on your screen:
| |
| | |
| <math></math>
| |
| [[Image:11260plot.png|thumb|center|400px| ]]
| |
| | |
| | |
| 8-3. From the Special Plot Type menu choose Pdf Plot. The following plot should appear on your screen.
| |
| | |
| [[Image:11260pdfplot.png|thumb|center|400px| ]]
| |
| <math></math>
| |
| | |
| ===Weibull Normal Distribution Example===
| |
| Using the data and results from the previous example (and RRX), do the following:
| |
| 9-1. Using the Quick Calculation Pad, determine the reliability for a mission of 11,000 hours, as well as the upper and lower two-sided 90% confidence limit on this reliability.
| |
| 9-2. Using the Quick Calculation Pad, determine the MTTF, as well as the upper and lower two-sided 90% confidence limit on this MTTF.
| |
| | |
| ==== Solutions====
| |
| Both of these results are easily obtained from the QCP. The QCP with results for both cases is shown in the next two figures.
| |
| | |
| {|align="center"
| |
| |-
| |
| |[[Image:qcpPOF.png|thumb|center|400px| ]] || [[Image:qcpmeanlife.png|thumb|center|400px| ]]
| |
| |}
| |
| | |
| ====Weibull Normal Distribution Example====
| |
| Using the data from Example 8, and using the rank regression on X analysis method (RRX), obtain tabulated values for the failure rate for 10 different mission end times. The mission end times are 1,000 to 10,000 hours, using increments of 1,000 hours.
| |
| ====Solution to Example 10====
| |
| This can be easily accomplished via the use of the Function Wizard, available in either Weibull++'s Reports or the General Spreadsheet. (For more information on these features, please refer to the Weibull++ User's Guide.) We will illustrate this using the General Spreadsheet.
| |
| | |
| First, click on Insert General Spread Sheet from the Folio menu.
| |
| | |
| [[Image:generalspreadsheeticon.png|thumb|center|400px]]
| |
| | |
| Type Time in cell A1 and Failure Rate in cell B1. Then enter 1000 through 10000 in cells A2 to A11. Finally, place the cursor into cell B2, as shown next.
| |
| | |
| [[Image:plainspreadsheet.png|thumb|center|400px| ]]
| |
| | |
| Open the Function Wizard by selecting Function Wizard from the Data menu or by clicking the Function Wizard icon.
| |
| | |
| [[Image:functionwizard.png|thumb|center|400px| ]]
| |
| | |
| Select FAILURERATE from the list of functions. Enter A2 for Time; this indicates that the time input for the equation will be obtained from the specified cell in the worksheet. To specify the existing Weibull++ analysis that the function result will be based on, click Select... to open the Select Folio/Data Sheet window and then navigate to the desired sheet.
| |
| | |
| [[Image:A2functionwizard.png|thumb|center|400px]]
| |
| | |
| [[Image:A2selectdatasheet.png|thumb|center|300px]]
| |
| | |
| Click OK to close the window and return to the Function Wizard. Click Add to Equation to update the box at the bottom of the window with the function code that will be inserted into the spreadsheet.
| |
| | |
| [[Image:functionwizardFR.png|thumb|center|400px]]
| |
| | |
| Click Insert to close the window and insert the function code into the active cell in the General Spreadsheet. Copy the function into cells B3 through B11. One way to do this is to position the mouse over the bottom right corner of cell B2 and when the cursor turns into a plus symbol (+), click and drag the mouse to cell B11. By selecting one of the cells that you copied the function into, you can see that the cell reference was updated to match the current row, as shown next with cell B11 selected. The results are as follows:
| |
| | |
| [[Image:folio^E.png|thumb|center|400px]]
| |
| | |
| ===Weibull Normal Distribution Example===
| |
| Eight units are being reliability tested and the following is a table of their times-to-failure:
| |
| | |
| | |
| {|align="center" border=1 cellspacing=1
| |
| |- | | |- |
| |colspan="3" style="text-align:center"| Table 8.3 - Non-Grouped Data Times-to-Failure with intervals (lnterval and left censored) | | |colspan="3" style="text-align:center"| '''Non-Grouped Interval Data''' |
| |- | | |- |
| !Data point index | | !Data point index |
| Line 378: |
Line 153: |
| |} | | |} |
|
| |
|
| ====Solution====
| |
| This is a sequence of interval times-to-failure. This data set can be entered into Weibull++ by creating a data sheet that can be used to analyze times-to-failure data with interval and left censored data.
| |
|
| |
|
| <math></math>
| | This is a sequence of interval times-to-failure data. Using the normal distribution and the maximum likelihood (MLE) parameter estimation method, the computed parameters are: |
| [[Image:lastinspected.png|thumb|center|400px| ]]
| |
| | |
| [[Image:lastinspectedsheet.png|thumb|center|400px]]
| |
| | |
| The computed parameters for maximum likelihood are:
| |
|
| |
|
| ::<math>\begin{align} | | ::<math>\begin{align} |
| & \widehat{\mu }= & 41.40 \\ | | & \widehat{\mu }= & 41.40 \\ |
| & {{{\hat{\sigma }}}_{T}}= & 7.740. | | & {{{\hat{\sigma }}}_{T}}= & 7.740. |
| \end{align}</math> | | \end{align}\,\!</math> |
| | |
|
| |
|
| For rank regression on x: | | For rank regression on x: |
| Line 398: |
Line 167: |
| & \widehat{\mu }= & 41.40 \\ | | & \widehat{\mu }= & 41.40 \\ |
| & {{{\hat{\sigma }}}_{T}}= & 9.03. | | & {{{\hat{\sigma }}}_{T}}= & 9.03. |
| \end{align}</math> | | \end{align}\,\!</math> |
|
| |
|
| For rank regression on y:
| | |
| | If we analyze the data set with the rank regression on y (RRY) parameter estimation method, the computed parameters are: |
|
| |
|
| ::<math>\begin{align} | | ::<math>\begin{align} |
| & \widehat{\mu }= & 41.39 \\ | | & \widehat{\mu }= & 41.39 \\ |
| & {{{\hat{\sigma }}}_{T}}= & 9.25. | | & {{{\hat{\sigma }}}_{T}}= & 9.25. |
| \end{align}</math> | | \end{align}\,\!</math> |
|
| |
|
|
| |
|
| A plot of the MLE solution is shown next.
| | The following plot shows the results if the data were analyzed using the rank regression on X (RRX) method. |
|
| |
|
| <math></math>
| |
| [[Image:lastinspectedplot.png|thumb|center|400px| ]]
| |
|
| |
|
| ===Weibull Normal Distribution Example===
| | [[Image:lastinspectedplot.png|center|600px| ]] |
| Eight units are being reliability tested and the following is a table of their times-to-failure:
| |
|
| |
|
| | ===Mixed Data Types Example=== |
| | Suppose our data set includes left and right censored, interval censored and complete data, as shown in the following table. |
|
| |
|
| {|align="center" border=1 cellspacing=1 | | {|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" |
| |- | | |- |
| |colspan="3" style="text-align:center"| Table 8.4 - Non-Grouped Data ,for Example 12
| | !colspan="5" style="text-align:center"| Grouped Data Times-to-Failure with Suspensions and Intervals (Interval, Left and Right Censored) |
| |- | | |- |
| !Data point index | | !Data point index |
| !State F or S | | !Number in State |
| | !Last Inspection |
| | !State (S or F) |
| !State End Time | | !State End Time |
| |- | | |- |
| |1 ||F||2 | | |1 ||1 ||10 ||F||10 |
| |- | | |- |
| |2 ||F||5 | | |2 ||1 ||20 ||S||20 |
| |- | | |- |
| |3 ||F||11 | | |3 ||2 ||0 ||F||30 |
| |- | | |- |
| |4 ||F||23 | | |4 ||2 ||40 ||F||40 |
| |- | | |- |
| |5 ||F||29 | | |5 ||1 ||50 ||F||50 |
| |- | | |- |
| |6 ||F||37 | | |6 ||1 ||60 ||S||60 |
| | |- |
| | |7 ||1 ||70 ||F||70 |
| |- | | |- |
| |7||F||43 | | |8 ||2 ||20 ||F||80 |
| |- | | |- |
| |8||F||59 | | |9 ||1 ||10 ||F||85 |
| | |- |
| | |10||1 ||100||F||100 |
| |} | | |} |
|
| |
|
| ==== Solution====
| | |
| This data set can be entered into Weibull++ by creating a Data Sheet appropriate for the entry of non-grouped times-to-failure data.
| | Using the normal distribution and the maximum likelihood (MLE) parameter estimation method, the computed parameters are: |
| The computed parameters for maximum likelihood are:
| |
|
| |
|
| ::<math>\begin{align} | | ::<math>\begin{align} |
| & \widehat{\mu }= & 26.13 \\ | | & \widehat{\mu }= & 48.11 \\ |
| & {{{\hat{\sigma }}}_{T}}= & 18.57 | | & {{{\hat{\sigma }}}_{T}}= & 26.42 |
| \end{align}</math> | | \end{align}\,\!</math> |
|
| |
|
|
| |
|
| For rank regression on x:
| | If we analyze the data set with the rank regression on x (RRX) method, the computed parameters are: |
|
| |
|
| ::<math>\begin{align} | | ::<math>\begin{align} |
| & \widehat{\mu }= & 26.13 \\ | | & \widehat{\mu }= & 49.99 \\ |
| & {{{\hat{\sigma }}}_{T}}= & 21.64 | | & {{{\hat{\sigma }}}_{T}}= & 30.17 |
| \end{align}</math> | | \end{align}\,\!</math> |
|
| |
|
|
| |
|
| For rank regression on y: | | For the rank regression on y (RRY) method, the parameters are: |
|
| |
|
| ::<math>\begin{align} | | ::<math>\begin{align} |
| & \widehat{\mu }= & 26.13 \\ | | & \widehat{\mu }= & 51.61 \\ |
| & {{{\hat{\sigma }}}_{T}}= & 22.28. | | & {{{\hat{\sigma }}}_{T}}= & 33.07 |
| \end{align}</math> | | \end{align}\,\!</math> |
| | | ===Comparison of Analysis Methods=== |
| ===Weibull Normal Distribution Example=== | | 8 units are being reliability tested, and the following is a table of their failure times: |
| Nineteen units are being reliability tested and the following is a table of their times-to-failure and suspensions.
| |
|
| |
|
| {|align="center" border=1 cellspacing=1 | | {|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" |
| |- | | |- |
| |colspan="3" style="text-align:center"| Table 8.5 - Non-Grouped Data Times-to-Failure with Suspensions (Right Censored) | | |colspan="3" style="text-align:center"| '''Non-Grouped Times-to-Failure Data''' |
| |- | | |- |
| !Data point index | | !Data point index |
| !Last Inspected | | !State F or S |
| !State End Time | | !State End Time |
| |- | | |- |
| |1 ||F||2 | | |1 ||F||2 |
| |- | | |- |
| |2 ||S||3 | | |2 ||F||5 |
| |- | | |- |
| |3 ||F||5 | | |3 ||F||11 |
| |- | | |- |
| |4 ||S||7 | | |4 ||F||23 |
| |- | | |- |
| |5 ||F||11 | | |5 ||F||29 |
| |- | | |- |
| |6 ||S||13 | | |6 ||F||37 |
| |- | | |- |
| |7||S||17 | | |7||F||43 |
| |- | | |- |
| |8||S||19 | | |8||F||59 |
| |-
| |
| |9 ||F||23
| |
| |-
| |
| |10 ||F||29
| |
| |-
| |
| |11 ||S||31
| |
| |-
| |
| |12 ||F||37
| |
| |-
| |
| |13 ||S||41
| |
| |-
| |
| |14 ||F||43
| |
| |-
| |
| |15||S||47
| |
| |-
| |
| |16||S||53
| |
| |-
| |
| |17||F||59
| |
| |-
| |
| |18||S||61
| |
| |-
| |
| |19||S||67
| |
| |} | | |} |
|
| |
| ==== Solution====
| |
| This augments the previous example by adding eleven suspensions to the data set. This data set can be entered into Weibull++ by selecting the data sheet for Times to Failure and with Right Censored Data (Suspensions).
| |
| The parameters using maximum likelihood are:
| |
|
| |
| ::<math>\begin{align}
| |
| & \widehat{\mu }= & 48.07 \\
| |
| & {{{\hat{\sigma }}}_{T}}= & 28.41.
| |
| \end{align}</math>
| |
|
| |
|
|
| |
|
| For rank regression on x:
| | Using the normal distribution and the maximum likelihood (MLE) parameter estimation method, the computed parameters are: |
|
| |
|
| ::<math>\begin{align} | | ::<math>\begin{align} |
| & \widehat{\mu }= & 46.40 \\ | | & \widehat{\mu }= & 26.13 \\ |
| & {{{\hat{\sigma }}}_{T}}= & 28.64. | | & {{{\hat{\sigma }}}_{T}}= & 18.57 |
| \end{align}</math> | | \end{align}\,\!</math> |
|
| |
|
|
| |
|
| For rank regression on y:
| | If we analyze the data set with the rank regression on x (RRX) method, the computed parameters are: |
|
| |
|
| ::<math>\begin{align} | | ::<math>\begin{align} |
| & \widehat{\mu }= & 47.34 \\ | | & \widehat{\mu }= & 26.13 \\ |
| & {{{\hat{\sigma }}}_{T}}= & 29.96. | | & {{{\hat{\sigma }}}_{T}}= & 21.64 |
| \end{align}</math> | | \end{align}\,\!</math> |
|
| |
|
| === Weibull Normal Distribution Example===
| |
| Suppose our data set includes left and right censored, interval censored and complete data as shown in the following table.
| |
|
| |
|
| ==== Solution====
| | For the rank regression on y (RRY) method, the parameters are: |
| This data set can be entered into Weibull++ by selecting the data type Times to Failure, with Right Censored Data (Suspensions), with Interval and Left Censored Data and with Grouped Observations.
| |
| | |
| The computed parameters using maximum likelihood are:
| |
|
| |
|
| ::<math>\begin{align} | | ::<math>\begin{align} |
| & \widehat{\mu }= & 48.11 \\ | | & \widehat{\mu }= & 26.13 \\ |
| & {{{\hat{\sigma }}}_{T}}= & 26.42.
| | & {{{\hat{\sigma }}}_{T}}= & 22.28. |
| \end{align}</math>
| | \end{align}\,\!</math> |
| | |
| | |
| For rank regression on x:
| |
| | |
| ::<math>\begin{align}
| |
| & \widehat{\mu }= & 49.99 \\
| |
| & {{{\hat{\sigma }}}_{T}}= & 30.17. | |
| \end{align}</math> | |
| | |
| | |
| For rank regression on y:
| |
| | |
| ::<math>\begin{align}
| |
| & \widehat{\mu }= & 51.61 \\
| |
| & {{{\hat{\sigma }}}_{T}}= & 33.07.
| |
| \end{align}</math>
| |
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
These examples appear in the Life Data Analysis Reference book.
The following examples illustrate the different types of life data that can be analyzed in Weibull++ using the normal distribution. For more information on the different types of life data, see Life Data Classification.
Complete Data Example
6 units are tested to failure. The following failure times data are obtained: 12125, 11260, 12080, 12825, 13550 and 14670 hours. Assuming that the data are normally distributed, do the following:
Objectives
- 1. Find the parameters for the data set, using the Rank Regression on X (RRX) parameter estimation method
- 2. Obtain the probability plot for the data with 90%, two-sided Type 1 confidence bounds.
- 3. Obtain the pdf plot for the data.
- 4. Using the Quick Calculation Pad (QCP), determine the reliability for a mission of 11,000 hours, as well as the upper and lower two-sided 90% confidence limit on this reliability.
- 5. Using the QCP, determine the MTTF, as well as the upper and lower two-sided 90% confidence limit on this MTTF.
- 6. Obtain tabulated values for the failure rate for 10 different mission end times. The mission end times are 1,000 to 10,000 hours, using increments of 1,000 hours.
Solution
The following figure shows the data as entered in Weibull++, as well as the calculated parameters.
The following figures show the probability plot with the 90% two-sided confidence bounds and the pdf plot.
Both the reliability and MTTF can be easily obtained from the QCP. The QCP, with results, for both cases is shown in the next two figures.
To obtain tabulated values for the failure rate, use the Analysis Workbook or General Spreadsheet features that are included in Weibull++. (For more information on these features, please refer to the Weibull++ User's Guide. For a step-by-step example on creating Weibull++ reports, please see the Quick Start Guide). The following worksheet shows the mission times and the corresponding failure rates.
Suspension Data Example
19 units are being reliability tested and the following is a table of their times-to-failure and suspensions.
| Non-Grouped Data Times-to-Failure Data with Suspensions
|
| Data point index
|
Last Inspected
|
State End Time
|
| 1 |
F |
2
|
| 2 |
S |
3
|
| 3 |
F |
5
|
| 4 |
S |
7
|
| 5 |
F |
11
|
| 6 |
S |
13
|
| 7 |
S |
17
|
| 8 |
S |
19
|
| 9 |
F |
23
|
| 10 |
F |
29
|
| 11 |
S |
31
|
| 12 |
F |
37
|
| 13 |
S |
41
|
| 14 |
F |
43
|
| 15 |
S |
47
|
| 16 |
S |
53
|
| 17 |
F |
59
|
| 18 |
S |
61
|
| 19 |
S |
67
|
Using the normal distribution and the maximum likelihood (MLE) parameter estimation method, the computed parameters are:
- [math]\displaystyle{ \begin{align}
& \widehat{\mu }= & 48.07 \\
& {{{\hat{\sigma }}}_{T}}= & 28.41.
\end{align}\,\! }[/math]
If we analyze the data set with the rank regression on x (RRX) method, the computed parameters are:
- [math]\displaystyle{ \begin{align}
& \widehat{\mu }= & 46.40 \\
& {{{\hat{\sigma }}}_{T}}= & 28.64.
\end{align}\,\! }[/math]
For the rank regression on y (RRY) method, the parameters are:
- [math]\displaystyle{ \begin{align}
& \widehat{\mu }= & 47.34 \\
& {{{\hat{\sigma }}}_{T}}= & 29.96.
\end{align}\,\! }[/math]
Interval Censored Data Example
8 units are being reliability tested, and the following is a table of their failure times:
| Non-Grouped Interval Data
|
| Data point index
|
Last Inspected
|
State End Time
|
| 1 |
30 |
32
|
| 2 |
32 |
35
|
| 3 |
35 |
37
|
| 4 |
37 |
40
|
| 5 |
42 |
42
|
| 6 |
45 |
45
|
| 7 |
50 |
50
|
| 8 |
55 |
55
|
This is a sequence of interval times-to-failure data. Using the normal distribution and the maximum likelihood (MLE) parameter estimation method, the computed parameters are:
- [math]\displaystyle{ \begin{align}
& \widehat{\mu }= & 41.40 \\
& {{{\hat{\sigma }}}_{T}}= & 7.740.
\end{align}\,\! }[/math]
For rank regression on x:
- [math]\displaystyle{ \begin{align}
& \widehat{\mu }= & 41.40 \\
& {{{\hat{\sigma }}}_{T}}= & 9.03.
\end{align}\,\! }[/math]
If we analyze the data set with the rank regression on y (RRY) parameter estimation method, the computed parameters are:
- [math]\displaystyle{ \begin{align}
& \widehat{\mu }= & 41.39 \\
& {{{\hat{\sigma }}}_{T}}= & 9.25.
\end{align}\,\! }[/math]
The following plot shows the results if the data were analyzed using the rank regression on X (RRX) method.
Mixed Data Types Example
Suppose our data set includes left and right censored, interval censored and complete data, as shown in the following table.
| Grouped Data Times-to-Failure with Suspensions and Intervals (Interval, Left and Right Censored)
|
| Data point index
|
Number in State
|
Last Inspection
|
State (S or F)
|
State End Time
|
| 1 |
1 |
10 |
F |
10
|
| 2 |
1 |
20 |
S |
20
|
| 3 |
2 |
0 |
F |
30
|
| 4 |
2 |
40 |
F |
40
|
| 5 |
1 |
50 |
F |
50
|
| 6 |
1 |
60 |
S |
60
|
| 7 |
1 |
70 |
F |
70
|
| 8 |
2 |
20 |
F |
80
|
| 9 |
1 |
10 |
F |
85
|
| 10 |
1 |
100 |
F |
100
|
Using the normal distribution and the maximum likelihood (MLE) parameter estimation method, the computed parameters are:
- [math]\displaystyle{ \begin{align}
& \widehat{\mu }= & 48.11 \\
& {{{\hat{\sigma }}}_{T}}= & 26.42
\end{align}\,\! }[/math]
If we analyze the data set with the rank regression on x (RRX) method, the computed parameters are:
- [math]\displaystyle{ \begin{align}
& \widehat{\mu }= & 49.99 \\
& {{{\hat{\sigma }}}_{T}}= & 30.17
\end{align}\,\! }[/math]
For the rank regression on y (RRY) method, the parameters are:
- [math]\displaystyle{ \begin{align}
& \widehat{\mu }= & 51.61 \\
& {{{\hat{\sigma }}}_{T}}= & 33.07
\end{align}\,\! }[/math]
Comparison of Analysis Methods
8 units are being reliability tested, and the following is a table of their failure times:
| Non-Grouped Times-to-Failure Data
|
| Data point index
|
State F or S
|
State End Time
|
| 1 |
F |
2
|
| 2 |
F |
5
|
| 3 |
F |
11
|
| 4 |
F |
23
|
| 5 |
F |
29
|
| 6 |
F |
37
|
| 7 |
F |
43
|
| 8 |
F |
59
|
Using the normal distribution and the maximum likelihood (MLE) parameter estimation method, the computed parameters are:
- [math]\displaystyle{ \begin{align}
& \widehat{\mu }= & 26.13 \\
& {{{\hat{\sigma }}}_{T}}= & 18.57
\end{align}\,\! }[/math]
If we analyze the data set with the rank regression on x (RRX) method, the computed parameters are:
- [math]\displaystyle{ \begin{align}
& \widehat{\mu }= & 26.13 \\
& {{{\hat{\sigma }}}_{T}}= & 21.64
\end{align}\,\! }[/math]
For the rank regression on y (RRY) method, the parameters are:
- [math]\displaystyle{ \begin{align}
& \widehat{\mu }= & 26.13 \\
& {{{\hat{\sigma }}}_{T}}= & 22.28.
\end{align}\,\! }[/math]