Distributions Used in Accelerated Testing: Difference between revisions
Lisa Hacker (talk | contribs) No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| Line 85: | Line 85: | ||
==Weibull Distribution Functions== | ==Weibull Distribution Functions== | ||
{{:Weibull Distribution Functions}} | {{:Weibull Distribution Functions}} | ||
==Characteristics== | ==Characteristics== | ||
The characteristics of the 2-parameter Weibull distribution can be exemplified by examining the two parameters, beta, <math>\beta ,</math> and eta, <math>\eta ,</math> and the effect they have on the <math>pdf,</math> reliability and failure rate functions. | The characteristics of the 2-parameter Weibull distribution can be exemplified by examining the two parameters, beta, <math>\beta ,</math> and eta, <math>\eta ,</math> and the effect they have on the <math>pdf,</math> reliability and failure rate functions. | ||
| Line 272: | Line 174: | ||
<br> | <br> | ||
= The Lognormal Distribution = | = The Lognormal Distribution = | ||
| Line 414: | Line 220: | ||
<br> | <br> | ||
==Lognormal Distribution Functions== | |||
{{:Lognormal Distribution Functions}} | |||
==Characteristics== | ==Characteristics== | ||
| Line 506: | Line 249: | ||
[[Image:chp4pdf3.png|center|400px|''Pdf'' of the lognormal distribution with different log-std values.]] | [[Image:chp4pdf3.png|center|400px|''Pdf'' of the lognormal distribution with different log-std values.]] | ||
<br> | <br> | ||
Revision as of 02:30, 7 August 2012
In this chapter, we will briefly present three lifetime distributions commonly used in accelerated life test analysis: the 1-parameter exponential, the 2-parameter Weibull and the lognormal distributions. Readers who are interested in a more rigorous overview (or in different forms of these and other life distributions) can refer to ReliaSoft's Life Data Analysis Reference. For information about the parameter estimation methods, see Appendix B.
The Exponential Distribution
The exponential distribution is a very commonly used distribution in reliability engineering. Due to its simplicity, it has been widely employed, even in cases where it doesn't apply. The exponential distribution is used to describe units that have a constant failure rate. The 1-parameter exponential pdf is given by:
- [math]\displaystyle{ \begin{align} & f(T)= \lambda {{e}^{-\lambda T}}=\frac{1}{m}{{e}^{-\tfrac{1}{m}T}} \\ & T\ge 0,\lambda \gt 0,m\gt 0 \end{align} }[/math]
where:
- λ = constant failure rate, in failures per unit of measurement (e.g. failures per hour, per cycle, etc.).
- [math]\displaystyle{ \lambda =\tfrac{1}{m} }[/math].
- m = mean time between failures, or to a failure.
- T = operating time, life, or age, in hours, cycles, miles, actuations, etc. This distribution requires the estimation of only one parameter, λ , for its application.
Exponential Distribution Functions
The Mean or MTTF
The mean, [math]\displaystyle{ \overline{T},\,\! }[/math] or mean time to failure (MTTF) is given by:
- [math]\displaystyle{ \begin{align} \bar{T}= & \int_{\gamma }^{\infty }t\cdot f(t)dt \\ = & \int_{\gamma }^{\infty }t\cdot \lambda \cdot {{e}^{-\lambda t}}dt \\ = & \gamma +\frac{1}{\lambda }=m \end{align}\,\! }[/math]
Note that when [math]\displaystyle{ \gamma =0\,\! }[/math], the MTTF is the inverse of the exponential distribution's constant failure rate. This is only true for the exponential distribution. Most other distributions do not have a constant failure rate. Consequently, the inverse relationship between failure rate and MTTF does not hold for these other distributions.
The Median
The median, [math]\displaystyle{ \breve{T}, \,\! }[/math] is:
- [math]\displaystyle{ \breve{T}=\gamma +\frac{1}{\lambda}\cdot 0.693 \,\! }[/math]
The Mode
The mode, [math]\displaystyle{ \tilde{T},\,\! }[/math] is:
- [math]\displaystyle{ \tilde{T}=\gamma \,\! }[/math]
The Standard Deviation
The standard deviation, [math]\displaystyle{ {\sigma }_{T}\,\! }[/math], is:
- [math]\displaystyle{ {\sigma}_{T}=\frac{1}{\lambda }=m\,\! }[/math]
The Exponential Reliability Function
The equation for the 2-parameter exponential cumulative density function, or cdf, is given by:
- [math]\displaystyle{ \begin{align} F(t)=Q(t)=1-{{e}^{-\lambda (t-\gamma )}} \end{align}\,\! }[/math]
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function of the 2-parameter exponential distribution is given by:
- [math]\displaystyle{ R(t)=1-Q(t)=1-\int_{0}^{t-\gamma }f(x)dx\,\! }[/math]
- [math]\displaystyle{ R(t)=1-\int_{0}^{t-\gamma }\lambda {{e}^{-\lambda x}}dx={{e}^{-\lambda (t-\gamma )}}\,\! }[/math]
The 1-parameter exponential reliability function is given by:
- [math]\displaystyle{ R(t)={{e}^{-\lambda t}}={{e}^{-\tfrac{t}{m}}}\,\! }[/math]
The Exponential Conditional Reliability Function
The exponential conditional reliability equation gives the reliability for a mission of [math]\displaystyle{ t\,\! }[/math] duration, having already successfully accumulated [math]\displaystyle{ T\,\! }[/math] hours of operation up to the start of this new mission. The exponential conditional reliability function is:
- [math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)}=\frac{{{e}^{-\lambda (T+t-\gamma )}}}{{{e}^{-\lambda (T-\gamma )}}}={{e}^{-\lambda t}}\,\! }[/math]
which says that the reliability for a mission of [math]\displaystyle{ t\,\! }[/math] duration undertaken after the component or equipment has already accumulated [math]\displaystyle{ T\,\! }[/math] hours of operation from age zero is only a function of the mission duration, and not a function of the age at the beginning of the mission. This is referred to as the memoryless property.
The Exponential Reliable Life Function
The reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}}\,\! }[/math], for the 1-parameter exponential distribution is:
- [math]\displaystyle{ R({{t}_{R}})={{e}^{-\lambda ({{t}_{R}}-\gamma )}}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \ln[R({{t}_{R}})]=-\lambda({{t}_{R}}-\gamma ) \end{align}\,\! }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=\gamma -\frac{\ln [R({{t}_{R}})]}{\lambda }\,\! }[/math]
The Exponential Failure Rate Function
The exponential failure rate function is:
- [math]\displaystyle{ \lambda (t)=\frac{f(t)}{R(t)}=\frac{\lambda {{e}^{-\lambda (t-\gamma )}}}{{{e}^{-\lambda (t-\gamma )}}}=\lambda =\text{constant}\,\! }[/math]
Once again, note that the constant failure rate is a characteristic of the exponential distribution, and special cases of other distributions only. Most other distributions have failure rates that are functions of time.
Characteristics
The characteristics of the 1-parameter exponential distribution can be exemplified by examining its parameter, lambda (λ) and the effect lambda has on the pdf, reliability and failure rate functions.
Effects of λ on the pdf
- The scale parameter is [math]\displaystyle{ \tfrac{1}{\lambda } }[/math] .
- As λ is decreased in value, the distribution is stretched out to the right, and as λ is increased, the distribution is pushed toward the origin.
- This distribution has no shape parameter, as it has only one shape (i.e., the exponential). Its only parameter is the failure rate, λ .
- The distribution starts at T = 0 at the level of f(T = 0) = λ. It decreases thereafter exponentially and monotonically as T increases, and it is convex.
- As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ f(T)\to 0 }[/math].
- This pdf can be thought of as a special case of the Weibull pdf with β = 1.
Effects of λ on the Reliability Function
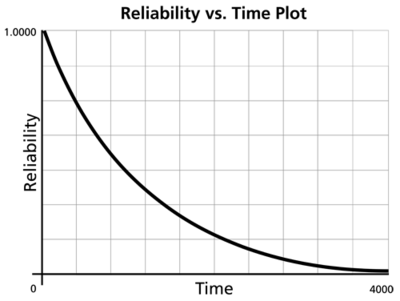
- The 1-parameter exponential reliability function starts at the value of 1 at T = 0 . It decreases thereafter monotonically and is convex.
- As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ R(T\to \infty )\to 0 }[/math].
Effects of λ on the Failure Rate Function
The failure rate function for the exponential distribution is constant and equal to the parameter λ .
The Weibull Distribution
The Weibull distribution is one of the most commonly used distributions in reliability engineering because of the many shapes it attains for various values of β (slope). It can therefore model a great variety of data and life characteristics [18].
The 2-parameter Weibull pdf is given by:
- [math]\displaystyle{ f(T)=\frac{\beta }{\eta }{{\left( \frac{T}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}} }[/math]
where:
- [math]\displaystyle{ f(T)\ge 0,\text{ }T\ge 0,\text{ }\beta \gt 0,\text{ }\eta \gt 0\text{ } }[/math]
and:
- η = scale parameter.
- β = shape parameter (or slope).
Weibull Distribution Functions
The Mean or MTTF
The mean, [math]\displaystyle{ \overline{T} \,\! }[/math], (also called MTTF) of the Weibull pdf is given by:
- [math]\displaystyle{ \overline{T}=\gamma +\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
where
- [math]\displaystyle{ \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
is the gamma function evaluated at the value of:
- [math]\displaystyle{ \left( { \frac{1}{\beta }}+1\right) \,\! }[/math]
The gamma function is defined as:
- [math]\displaystyle{ \Gamma (n)=\int_{0}^{\infty }e^{-x}x^{n-1}dx \,\! }[/math]
For the 2-parameter case, this can be reduced to:
- [math]\displaystyle{ \overline{T}=\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
Note that some practitioners erroneously assume that [math]\displaystyle{ \eta \,\! }[/math] is equal to the MTTF, [math]\displaystyle{ \overline{T}\,\! }[/math]. This is only true for the case of: [math]\displaystyle{ \beta=1 \,\! }[/math] or:
- [math]\displaystyle{ \begin{align} \overline{T} &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\ &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\ &= \eta \cdot \Gamma \left( {2}\right) \\ &= \eta \cdot 1\\ &= \eta \end{align} \,\! }[/math]
The Median
The median, [math]\displaystyle{ \breve{T}\,\! }[/math], of the Weibull distribution is given by:
- [math]\displaystyle{ \breve{T}=\gamma +\eta \left( \ln 2\right) ^{\frac{1}{\beta }} \,\! }[/math]
The Mode
The mode, [math]\displaystyle{ \tilde{T} \,\! }[/math], is given by:
- [math]\displaystyle{ \tilde{T}=\gamma +\eta \left( 1-\frac{1}{\beta }\right) ^{\frac{1}{\beta }} \,\! }[/math]
The Standard Deviation
The standard deviation, [math]\displaystyle{ \sigma _{T}\,\! }[/math], is given by:
- [math]\displaystyle{ \sigma _{T}=\eta \cdot \sqrt{\Gamma \left( {\frac{2}{\beta }}+1\right) -\Gamma \left( {\frac{1}{ \beta }}+1\right) ^{2}} \,\! }[/math]
The Weibull Reliability Function
The equation for the 3-parameter Weibull cumulative density function, cdf, is given by:
- [math]\displaystyle{ F(t)=1-e^{-\left( \frac{t-\gamma }{\eta }\right) ^{\beta }} \,\! }[/math]
This is also referred to as unreliability and designated as [math]\displaystyle{ Q(t) \,\! }[/math] by some authors.
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function for the 3-parameter Weibull distribution is then given by:
- [math]\displaystyle{ R(t)=e^{-\left( { \frac{t-\gamma }{\eta }}\right) ^{\beta }} \,\! }[/math]
The Weibull Conditional Reliability Function
The 3-parameter Weibull conditional reliability function is given by:
- [math]\displaystyle{ R(t|T)={ \frac{R(T+t)}{R(T)}}={\frac{e^{-\left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }}}{e^{-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }}}} \,\! }[/math]
or:
- [math]\displaystyle{ R(t|T)=e^{-\left[ \left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }\right] } \,\! }[/math]
These give the reliability for a new mission of [math]\displaystyle{ t \,\! }[/math] duration, having already accumulated [math]\displaystyle{ T \,\! }[/math] time of operation up to the start of this new mission, and the units are checked out to assure that they will start the next mission successfully. It is called conditional because you can calculate the reliability of a new mission based on the fact that the unit or units already accumulated hours of operation successfully.
The Weibull Reliable Life
The reliable life, [math]\displaystyle{ T_{R}\,\! }[/math], of a unit for a specified reliability, [math]\displaystyle{ R\,\! }[/math], starting the mission at age zero, is given by:
- [math]\displaystyle{ T_{R}=\gamma +\eta \cdot \left\{ -\ln ( R ) \right\} ^{ \frac{1}{\beta }} \,\! }[/math]
This is the life for which the unit/item will be functioning successfully with a reliability of [math]\displaystyle{ R\,\! }[/math]. If [math]\displaystyle{ R = 0.50\,\! }[/math], then [math]\displaystyle{ T_{R}=\breve{T} \,\! }[/math], the median life, or the life by which half of the units will survive.
The Weibull Failure Rate Function
The Weibull failure rate function, [math]\displaystyle{ \lambda(t) \,\! }[/math], is given by:
- [math]\displaystyle{ \lambda \left( t\right) = \frac{f\left( t\right) }{R\left( t\right) }=\frac{\beta }{\eta }\left( \frac{ t-\gamma }{\eta }\right) ^{\beta -1} \,\! }[/math]
Characteristics
The characteristics of the 2-parameter Weibull distribution can be exemplified by examining the two parameters, beta, [math]\displaystyle{ \beta , }[/math] and eta, [math]\displaystyle{ \eta , }[/math] and the effect they have on the [math]\displaystyle{ pdf, }[/math] reliability and failure rate functions.
Looking at β
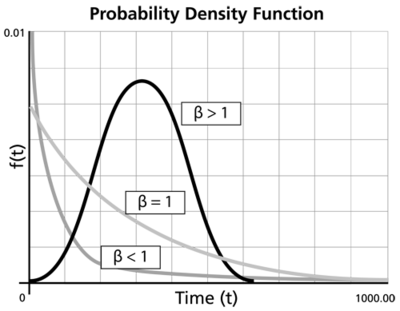
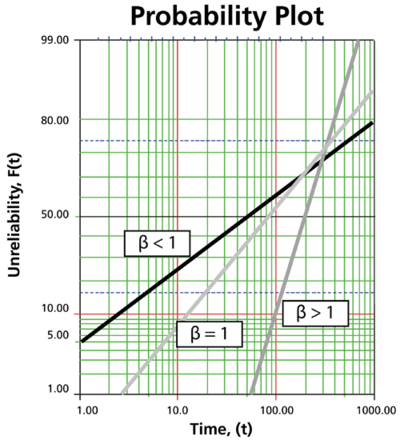
Beta (β) is called the shape parameter or slope of the Weibull distribution. Changing the value of β forces a change in the shape of the pdf as shown in the next figure. In addition, when the cdf is plotted on Weibull probability paper, a change in beta is a change in the slope of the distribution on Weibull probability paper.
Effects of β on the pdf
- For 0 < β < 1 , the failure rate decreases with time and:
- As [math]\displaystyle{ T\to 0, }[/math] [math]\displaystyle{ f(T)\to \infty }[/math].
- As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ f(T)\to 0 }[/math].
- f(T) decreases monotonically and is convex as T increases.
- The mode is non-existent.
- For β = 1, it becomes the exponential distribution, as a special case,
- or:
- [math]\displaystyle{ f(T)=\frac{1}{\eta }{{e}^{-\tfrac{T}{\eta }}};\text{ }\eta \gt 0,T\ge 0 }[/math]
- where [math]\displaystyle{ \tfrac{1}{\eta }=\lambda = }[/math] chance, useful life, or failure rate.
- For β > 1, f(T), the Weibull distribution assumes wear-out type shapes (i.e., the failure rate increases with time) and:
- f(T) = 0 at T = 0 .
- f(T) increases as [math]\displaystyle{ T\to \tilde{T} }[/math] (mode) and decreases thereafter.
- For β = 2 it becomes the Rayleigh distribution as a special case. For β < 2.6, the Weibull pdf is positively skewed (has a right tail). For 2.6 < β < 3.7, its coefficient of skewness approaches zero (no tail). Consequently, it may approximate the normal pdf, and for β > 3.7 it is negatively skewed (left tail).
- The parameter β is a pure number (i.e., it is dimensionless).
Effects of β on the Reliability Function and the cdf
- R(T) decreases sharply and monotonically for 0 < β < 1. It is convex and decreases less sharply for the same β.
- For β = 1 and the same η, R(T) decreases monotonically but less sharply than for 0 < β < 1, and it is convex.
- For β > 1, R(T) decreases as T increases but less sharply than before. As wear-out sets in, it decreases sharply and goes through an inflection point.
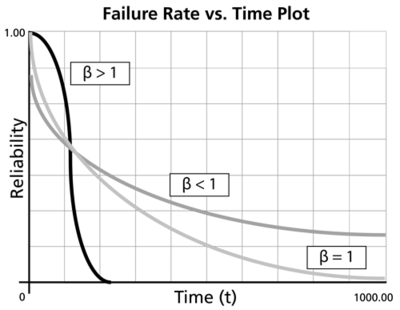
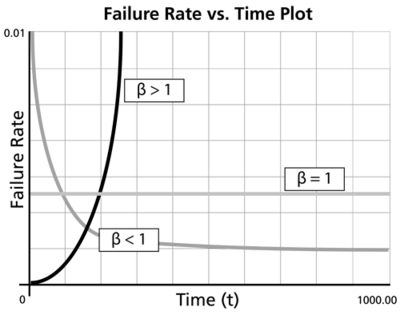
Effects of β on the Failure Rate Function
- The Weibull failure rate for 0 < β < 1 is unbounded at T = 0. The failure rate, λ(T), decreases thereafter monotonically and is convex, approaching the value of zero as [math]\displaystyle{ T\to \infty }[/math] or [math]\displaystyle{ \lambda (\infty )=0 }[/math]. This behavior makes it suitable for representing the failure rate of units exhibiting early-type failures, for which the failure rate decreases with age. When such behavior is encountered, one or more of the following conclusions can be drawn:
- Burn-in testing and/or environmental stress screening are not well implemented.
- There are problems in the production line.
- There is inadequate quality control.
- There are packaging and transit problems.
- For β = 1, λ(T) yields a constant value of [math]\displaystyle{ \tfrac{1}{\eta } }[/math] , or:
- [math]\displaystyle{ \lambda (T)=\lambda =\frac{1}{\eta } }[/math]
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units.
- For β > 1, λ(T) increases as T increases and becomes suitable for representing the failure rate of units exhibiting wear-out type failures. For 1 < β < 2, the λ(T) curve is concave. Consequently, the failure rate increases at a decreasing rate as T increases.
- For β = 2, or for the Rayleigh distribution case, the failure rate function is given by:
- [math]\displaystyle{ \lambda (T)=\frac{2}{\eta }\left( \frac{T}{\eta } \right) }[/math]
Hence there emerges a straight line relationship between λ(T) and T, starting at a value of λ(T) = 0 at T = 0 and increasing thereafter with a slope of [math]\displaystyle{ \tfrac{2}{{{\eta }^{2}}} }[/math] . Consequently, the failure rate increases at a constant rate as T increases. Furthermore, if η = 1 the slope becomes equal to 2, and λ(T) becomes a straight line which passes through the origin with a slope of 2.
- When β > 2 the λ(T) curve is convex, with its slope increasing as T increases. Consequently, the failure rate increases at an increasing rate as T increases, indicating wear-out life.
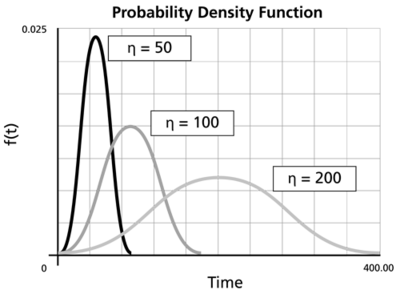
Looking at η
Eta (η) is called the scale parameter of the Weibull distribution. The parameter η has the same units as T, such as hours, miles, cycles, actuations, etc.
- A change in the scale parameter η has the same effect on the distribution as a change of the abscissa scale.
- If η is increased while β is kept the same, the distribution gets stretched out to the right and its height decreases, while maintaining its shape and location.
- If η is decreased while β is kept the same, the distribution gets pushed in toward the left (i.e. toward its beginning, or 0) and its height increases.
The Lognormal Distribution
The lognormal distribution is commonly used for general reliability analysis, cycles-to-failure in fatigue, material strengths and loading variables in probabilistic design. A random variable is lognormally distributed if the logarithm of the random variable is normally distributed. Since the logarithms of a lognormally distributed random variable are normally distributed, the lognormal distribution is given by:
- [math]\displaystyle{ f({T}')=\frac{1}{{{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\bar{{T}'}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}} }[/math]
where:
- T' = ln T, and where the Ts are the failure times.
- [math]\displaystyle{ \bar{{T}'}= }[/math] mean of the natural logarithms of the times to failure.
- σT' = standard deviation of the natural logarithms of the failure times.
The lognormal pdf can be obtained, realizing that for equal probabilities under the normal and lognormal pdf s incremental areas should also be equal, or:
- [math]\displaystyle{ \begin{align} f(T)dT = f(T')dT' \end{align} }[/math]
Taking the derivative yields:
- [math]\displaystyle{ d{T}'=\frac{dT}{T} }[/math]
Substitution yields:
- [math]\displaystyle{ \begin{align} f(T)= \frac{f({T}')}{T}= \frac{1}{T\cdot {{\sigma }_{{{T}'}}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{T}'-\bar{{T}'}}{{{\sigma }_{{{T}'}}}} \right)}^{2}}}} \end{align} }[/math]
where:
- [math]\displaystyle{ f(T)\ge 0,T\gt 0,-\infty \lt \bar{{T}'}\lt \infty ,{{\sigma }_{{{T}'}}}\gt 0 }[/math]
Lognormal Distribution Functions
The Mean or MTTF
The mean of the lognormal distribution, [math]\displaystyle{ \mu \,\! }[/math], is discussed in Kececioglu [19]:
- [math]\displaystyle{ \mu ={{e}^{{\mu }'+\tfrac{1}{2}\sigma'^{2}}}\,\! }[/math]
The mean of the natural logarithms of the times-to-failure, [math]\displaystyle{ \mu'\,\! }[/math], in terms of [math]\displaystyle{ \bar{T}\,\! }[/math] and [math]\displaystyle{ {{\sigma}}\,\! }[/math] is given by:
- [math]\displaystyle{ {\mu }'=\ln \left( {\bar{T}} \right)-\frac{1}{2}\ln \left( \frac{\sigma^{2}}{{{{\bar{T}}}^{2}}}+1 \right)\,\! }[/math]
The Median
The median of the lognormal distribution, [math]\displaystyle{ \breve{T}\,\! }[/math], is discussed in Kececioglu [19]:
- [math]\displaystyle{ \breve{T}={{e}^{{{\mu}'}}}\,\! }[/math]
The Mode
The mode of the lognormal distribution, [math]\displaystyle{ \tilde{T}\,\! }[/math], is discussed in Kececioglu [19]:
- [math]\displaystyle{ \tilde{T}={{e}^{{\mu }'-\sigma'^{2}}}\,\! }[/math]
The Standard Deviation
The standard deviation of the lognormal distribution, [math]\displaystyle{ {\sigma }_{T}\,\! }[/math], is discussed in Kececioglu [19]:
- [math]\displaystyle{ {\sigma}_{T} =\sqrt{\left( {{e}^{2\mu '+\sigma {{'}^{2}}}} \right)\left( {{e}^{\sigma {{'}^{2}}}}-1 \right)}\,\! }[/math]
The standard deviation of the natural logarithms of the times-to-failure, [math]\displaystyle{ {\sigma}'\,\! }[/math], in terms of [math]\displaystyle{ \bar{T}\,\! }[/math] and [math]\displaystyle{ {\sigma}\,\! }[/math] is given by:
- [math]\displaystyle{ \sigma '=\sqrt{\ln \left( \frac{{\sigma}_{T}^{2}}{{{{\bar{T}}}^{2}}}+1 \right)}\,\! }[/math]
The Lognormal Reliability Function
The reliability for a mission of time [math]\displaystyle{ t\,\! }[/math], starting at age 0, for the lognormal distribution is determined by:
- [math]\displaystyle{ R(t)=\int_{t}^{\infty }f(x)dx\,\! }[/math]
or:
- [math]\displaystyle{ {{R}({t})}=\int_{\text{ln}(t)}^{\infty }\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx\,\! }[/math]
As with the normal distribution, there is no closed-form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables. Since the application automatically solves for the reliability we will not discuss manual solution methods. For interested readers, full explanations can be found in the references.
The Lognormal Conditional Reliability Function
The lognormal conditional reliability function is given by:
- [math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)}=\frac{\int_{\text{ln}(T+t)}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}ds}{\int_{\text{ln}(T)}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx}\,\! }[/math]
Once again, the use of standard normal tables is necessary to solve this equation, as no closed-form solution exists.
The Lognormal Reliable Life Function
As there is no closed-form solution for the lognormal reliability equation, no closed-form solution exists for the lognormal reliable life either. In order to determine this value, one must solve the following equation for [math]\displaystyle{ t\,\! }[/math]:
- [math]\displaystyle{ {{R}_{t}}=\int_{\text{ln}(t)}^{\infty }\frac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{x-{\mu }'}{{{\sigma' }}} \right)}^{2}}}}dx\,\! }[/math]
The Lognormal Failure Rate Function
The lognormal failure rate is given by:
- [math]\displaystyle{ \lambda (t)=\frac{f(t)}{R(t)}=\frac{\tfrac{1}{t\cdot {{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{(\tfrac{{t}'-{\mu }'}{{{\sigma' }}})}^{2}}}}}{\int_{{{t}'}}^{\infty }\tfrac{1}{{{\sigma' }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{(\tfrac{x-{\mu }'}{{{\sigma' }}})}^{2}}}}dx}\,\! }[/math]
As with the reliability equations, standard normal tables will be required to solve for this function.
Characteristics
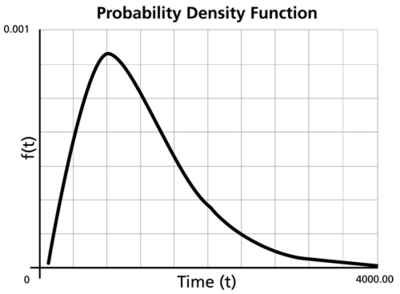
- The lognormal distribution is a distribution skewed to the right.
- The [math]\displaystyle{ pdf }[/math] starts at zero, increases to its mode, and decreases thereafter.
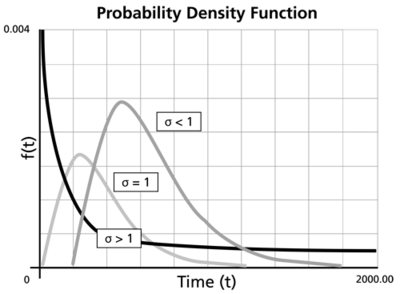
The characteristics of the lognormal distribution can be exemplified by examining the two parameters, the log-mean [math]\displaystyle{ ({{\overline{T}}^{\prime }}) }[/math] and the log-std ([math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math]), and the effect they have on the [math]\displaystyle{ pdf }[/math].
Looking at the Log-Mean [math]\displaystyle{ ({{\overline{T}}^{\prime }}) }[/math]
- The parameter, [math]\displaystyle{ \bar{{T}'} }[/math], or the log-mean life, or the [math]\displaystyle{ MTT{F}' }[/math] in terms of the logarithm of the [math]\displaystyle{ {T}'s }[/math] is also the scale parameter and a unitless number.
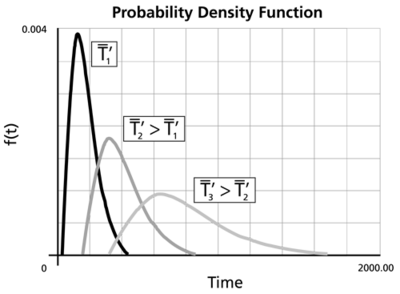
- For the same [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] the [math]\displaystyle{ pdf }[/math] 's skewness increases as [math]\displaystyle{ \bar{{T}'} }[/math] increases.
Looking at the Log-STD [math]\displaystyle{ ({{\sigma }_{{{T}'}}}) }[/math]
- The parameter [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math], or the standard deviation of the [math]\displaystyle{ {T}'s }[/math] in terms of their logarithm or of their [math]\displaystyle{ {T}' }[/math], is also the shape parameter, and not the scale parameter as in the normal [math]\displaystyle{ pdf }[/math]. It is a unitless number and assumes only positive values.
- The degree of skewness increases as [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] increases, for a given [math]\displaystyle{ \bar{{T}'} }[/math].
- For [math]\displaystyle{ {{\sigma }_{{{T}'}}} }[/math] values significantly greater than 1, the [math]\displaystyle{ pdf }[/math] rises very sharply in the beginning (i.e., for very small values of [math]\displaystyle{ T }[/math] near zero), and essentially follows the ordinate axis, peaks out early, and then decreases sharply like an exponential [math]\displaystyle{ pdf }[/math] or a Weibull [math]\displaystyle{ pdf }[/math] with [math]\displaystyle{ 0\lt \beta \lt 1 }[/math].