Basic Statistical Background: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(3 intermediate revisions by the same user not shown)
Line 1: Line 1:
{{template:LDABOOK|2|Basic Statistical Background}}
{{template:LDABOOK|2|Basic Statistical Background}}
This section provides a brief elementary introduction to the most common and fundamental statistical equations and definitions used in reliability engineering and life data analysis.  
This section provides a brief elementary introduction to the most common and fundamental statistical equations and definitions used in reliability engineering and life data analysis.  


=Random Variables=
{{:Brief_Statistical_Background}}
In general, most problems in reliability engineering deal with quantitative measures, such as the time-to-failure of a component, or whether the component fails or does not fail. In judging a component to be defective or non-defective, only two outcomes are possible. We can then denote a ''random variable'' ''X'' as representative of these possible outcomes (i.e. defective or non-defective). In this case, ''X'' is a random variable that can only take on these values.
 
In the case of times-to-failure, our random variable ''X'' can take on the time-to-failure (or time to an event of interest) of the product or component and can be in a range from ''0'' to infinity (since we do not know the exact time ''a priori'').
 
In the first case, where the random variable can take on only two discrete values (let's say ''defective =0'' and ''non-defective=1''), the variable is said to be a ''discrete random variable''. In the second case, our product can be found failed at any time after time ''0'', i.e. at ''12.4 hours'' or at ''100.12 miles'' and so forth, thus ''X'' can take on any value in this range. In this case, our random variable ''X'' is said to be a ''continuous random variable''.
 
==The Probability Density and Cumulative Distribution Functions==
'''Designations'''
 
From probability and statistics, given a continuous random variable,  we denote:
 
:*The probability density  function, ''pdf'', as ''f(x)''.
:*The cumulative distribution  function, ''cdf'', as ''F(x)''.
 
The ''pdf'' and ''cdf'' give a complete description of the probability distribution of a random variable.
 
 
'''Definitions'''
 
If <math>X</math> is a continuous random variable, then the probability density function, <math>pdf</math>, of <math>X</math>, is a function <math>f(x)</math> such that for two numbers, <math>a</math> and <math>b</math> with <math>a\le b</math>:
 
::<math>P(a \le X \le b)=\int_a^b f(x)dx</math>  and  <math>f(x)\ge 0 </math> for all x.
 
That is, the probability that takes on a value in the interval [a,b] is the area under the density function from <math>a</math> to <math>b</math>.
The cumulative distribution function, <math>cdf</math>, is a function <math>F(x)</math> of a random variable, <math>X</math>, and is defined for a number <math>x</math> by:
 
[[Image:pdf_cdf.png|center|200px|]]
 
::<math>F(x)=P(X\le x)=\int_0^x f(s)ds </math>
 
That is, for a given value <math>x</math>, <math>F(x)</math> is the probability that the observed value of <math>X</math> will be at most <math>x</math>.
Note that the limits of integration depend on the domain of <math>f(x)</math>. For example, for all the distributions considered in this reference, this domain would be <math>[0,+\infty]</math>,  <math>[-\infty ,+\infty]</math> or <math>[\gamma ,+\infty]</math>. In the case of <math>[\gamma ,+\infty ]</math>, we use the constant <math>\gamma </math> to denote an arbitrary non-zero point (or a location that indicates the starting point for the distribution). The next figure illustrates the relationship between the probability density function and the cumulative distribution function.
<br>
<br>
[[Image:pdf_cdf2.png|200px|center]]
 
'''Mathematical Relationship Between the <math>pdf</math> and <math>cdf</math>'''
 
The mathematical relationship between the <math>pdf</math> and <math>cdf</math> is given by:
 
::<math>F(x)=\int_{-\infty }^x f(s)ds</math>
 
Conversely:
 
::<math>f(x)=\frac{d(F(x))}{dx}</math>
 
In plain English, the value of the <math>cdf</math> at <math>x</math> is the area under the probability density function up to <math>x</math>, if so chosen. It should also be pointed out that the '''total area under the ''' <math>pdf</math>  '''is always equal to 1''', or mathematically:
 
::<math>\int_{-\infty }^{\infty }f(x)dx=1</math>
 
 
[[Image:100_percent.png|center|200px|]]
 
 
An example of a probability density function is the well-known normal distribution, whose <math>pdf</math> is given by:
 
::<math>f(t)={\frac{1}{\sigma \sqrt{2\pi }}}{e^{-\frac{1}{2}}(\frac{t-\mu}{\sigma})^2}</math>
 
where <math>\mu </math> is the mean and <math>\sigma</math> is the standard deviation. The normal distribution is a ''two-parameter distribution'', ''i.e.'' with two parameters <math>\mu </math> and <math>\sigma </math>.
Another two-parameter distribution is the lognormal distribution, whose  <math>pdf</math>  is given by:
 
::<math>f(t)=\frac{1}{t\cdot {{\sigma }^{\prime }}\sqrt{2\pi }}{e}^{-\tfrac{1}{2}(\tfrac{t^{\prime}-{\mu^{\prime}}}{\sigma^{\prime}})^2}</math>
 
where <math> t^{\prime}</math> is the natural logarithm of the times-to-failure, <math>\mu^{\prime}</math> is the mean of the natural logarithms of the times-to-failure and <math>\sigma^{\prime}</math> is the standard deviation of the natural logarithms of the times-to-failure, <math> t^{\prime }</math>.
 
 
 
=Functions Used in Reliability Engineerng=
 
===The Reliability Function===
 
The reliability function can be derived using the previous definition of the cumulative distribution function. The probability of an event happening by time <math>t</math> is given by:
 
::<math>F(t)=\int_{0,\gamma}^{t}f(s)ds</math>
 
In particular, this represents the probability of a unit failing by time <math>t</math>.
From this, we obtain the most commonly used function in reliability engineering, the reliability function, which represents the probability of success of a unit in undertaking a mission of a prescribed duration.
To mathematically show this, we first define the unreliability function, <math>Q(t)</math>, which is the probability of failure, or the probability that our time-to-failure is in the region of <math>0</math> (or <math>\gamma </math>) and <math>t</math>. So from the previous equation:
 
::<math>F(t)=Q(t)=\int_{0,\gamma}^{t}f(s)ds</math>
 
[[Image:reliabilityfunction.png|center|200px|]]
 
In this situation, there are only two states that can occur: success or failure. These two states are also mutually exclusive. Since reliability and unreliability are the probabilities of these two mutually exclusive states, the sum of these probabilities is always equal to unity. So then:
 
::<math>\begin{align}
    Q(t)+R(t)& =  1 \\
        R(t) & =  1-Q(t) \\
        R(t) & =  1-\int_{0,\gamma}^{t}f(s)ds \\
        R(t) & =  \int_{t}^{\infty }f(s)ds 
\end{align}</math>
 
Conversely:
 
::<math>f(t)=-\frac{d(R(t))}{dt}</math>
 
 
===The Conditional Reliability Function===
 
The reliability function discussed previously assumes that the unit is starting the mission with no accumulated time, i.e. brand new. Conditional reliability calculations allow one to calculate the probability of a unit successfully completing a mission of a particular duration given that it has already successfully completed a mission of a certain duration. In this respect, the conditional reliability function could be considered to be the ''reliability of used equipment''.
 
[[Image:missiontimeresult.png|center|250px|]]
 
The conditional reliability function is given by the equation:
 
::<math>R(t|T)=\frac{R(T+t)}{R(T)}</math>
 
where:
::* ''t'' is the duration of the new mission, and
::*''T''  is the duration of the successfully completed previous mission.
 
In other words, the fact that the equipment has already successfully completed a mission, <math>T</math>, tells us that the product successfully traversed the failure rate path for the period from <math>0\to T</math>, and it will now be failing according to the failure rate from <math>T\to T+t</math> <sup></sup>. An easier way to think about this is as the reliability of used equipment.
 
 
===The Failure Rate Function===
The failure rate function enables the determination of the number of failures occurring per unit time. The failure rate function is mathematically given as,
 
::<math>\begin{align}
  \lambda(t) & =  \frac{f(t)}{1-\int_{0,\gamma}^{t}f(s)ds} \\
& = \frac{f(t)}{R(t)}  \\
\end{align}</math>
 
The failure rate function has the units of failures per unit time among survivin units (e.g., 1 failure per month). The term "Hazard Rate" has also been used to refer to the failure rate by some authors.
 
 
===The Mean Life Function===
 
The mean life function, which provides a measure of the average time of operation to failure, is given by:
 
::<math>\mu = m =\int_{0,\gamma}^{\infty}t\cdot f(t)dt</math>
 
It should be noted that this is the expected or average time-to-failure and is denoted as the ''MTBF'' (Mean-Time-Before Failure) and is also called ''MTTF'' (Mean-Time-To-Failure) by many authors.
 
 
===The Median Life Function===
Median life,<math>\breve{T}</math> is the value of the random variable that has exactly one-half of the area under the <math>pdf</math> to its left and one-half to its right. The median is obtained from:
 
::<math>\int_{-\infty}^{\breve{T}}f(t)dt=0.5</math>
 
For sample data (e.g., 12, 20, 21), the median is the midpoint value, or 20 in this case.
 
 
===The Mode Function===
The modal (or mode) life, is the maximum value of  <math>T</math>  that satisfies:
 
::<math>\frac{d\left[ f(t) \right]}{dt}=0</math>
 
For a continuous distribution, the mode is that value of the variate which corresponds to the maximum probability density (the value where the <math>pdf</math> has its maximum value).<sup></sup>
 
 
 
 
 
[[Category: Completed Theoretical Review]]

Latest revision as of 09:16, 1 August 2012

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images, more targeted search and the latest content available as a PDF. As of September 2023, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest reference at help.reliasoft.com/reference/life_data_analysis

Chapter 2: Basic Statistical Background


Weibullbox.png

Chapter 2  
Basic Statistical Background  

Synthesis-icon.png

Available Software:
Weibull++

Examples icon.png

More Resources:
Weibull++ Examples Collection

This section provides a brief elementary introduction to the most common and fundamental statistical equations and definitions used in reliability engineering and life data analysis.


Random Variables


Chp3randomvariables.png


In general, most problems in reliability engineering deal with quantitative measures, such as the time-to-failure of a component, or qualitative measures, such as whether a component is defective or non-defective. We can then use a random variable [math]\displaystyle{ X\,\! }[/math] to denote these possible measures.

In the case of times-to-failure, our random variable [math]\displaystyle{ X\,\! }[/math] is the time-to-failure of the component and can take on an infinite number of possible values in a range from 0 to infinity (since we do not know the exact time a priori). Our component can be found failed at any time after time 0 (e.g., at 12 hours or at 100 hours and so forth), thus [math]\displaystyle{ X\,\! }[/math] can take on any value in this range. In this case, our random variable [math]\displaystyle{ X\,\! }[/math] is said to be a continuous random variable. In this reference, we will deal almost exclusively with continuous random variables.

In judging a component to be defective or non-defective, only two outcomes are possible. That is, [math]\displaystyle{ X\,\! }[/math] is a random variable that can take on one of only two values (let's say defective = 0 and non-defective = 1). In this case, the variable is said to be a discrete random variable.

The Probability Density Function and the Cumulative Distribution Function

The probability density function (pdf) and cumulative distribution function (cdf) are two of the most important statistical functions in reliability and are very closely related. When these functions are known, almost any other reliability measure of interest can be derived or obtained. We will now take a closer look at these functions and how they relate to other reliability measures, such as the reliability function and failure rate.

From probability and statistics, given a continuous random variable [math]\displaystyle{ X,\,\! }[/math] we denote:

  • The probability density function, pdf, as [math]\displaystyle{ f(x)\,\! }[/math].
  • The cumulative distribution function, cdf, as [math]\displaystyle{ F(x)\,\! }[/math].

The pdf and cdf give a complete description of the probability distribution of a random variable. The following figure illustrates a pdf.

Example of a pdf.

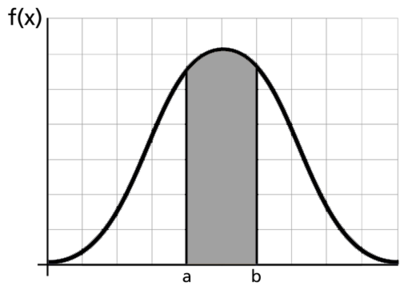
The next figures illustrate the pdf - cdf relationship.

Graphical representation of the relationship between pdf and cdf.

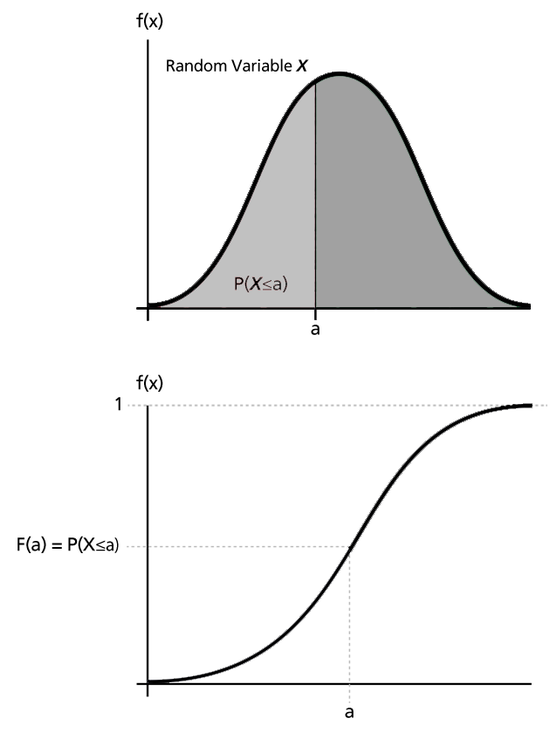
If [math]\displaystyle{ X\,\! }[/math] is a continuous random variable, then the pdf of [math]\displaystyle{ X\,\! }[/math] is a function, [math]\displaystyle{ f(x)\,\! }[/math], such that for any two numbers, [math]\displaystyle{ a\,\! }[/math] and [math]\displaystyle{ b\,\! }[/math] with [math]\displaystyle{ a\le b\,\! }[/math] :

[math]\displaystyle{ P(a\le X\le b)=\int_{a}^{b}f(x)dx\ \,\! }[/math]

That is, the probability that [math]\displaystyle{ X\,\! }[/math] takes on a value in the interval [math]\displaystyle{ [a,b]\,\! }[/math] is the area under the density function from [math]\displaystyle{ a\,\! }[/math] to [math]\displaystyle{ b,\,\! }[/math] as shown above. The pdf represents the relative frequency of failure times as a function of time.

The cdf is a function, [math]\displaystyle{ F(x)\,\! }[/math], of a random variable [math]\displaystyle{ X\,\! }[/math], and is defined for a number [math]\displaystyle{ x\,\! }[/math] by:

[math]\displaystyle{ F(x)=P(X\le x)=\int_{0}^{x}f(s)ds\ \,\! }[/math]

That is, for a number [math]\displaystyle{ x\,\! }[/math], [math]\displaystyle{ F(x)\,\! }[/math] is the probability that the observed value of [math]\displaystyle{ X\,\! }[/math] will be at most [math]\displaystyle{ x\,\! }[/math]. The cdf represents the cumulative values of the pdf. That is, the value of a point on the curve of the cdf represents the area under the curve to the left of that point on the pdf. In reliability, the cdf is used to measure the probability that the item in question will fail before the associated time value, [math]\displaystyle{ t\,\! }[/math], and is also called unreliability.

Note that depending on the density function, denoted by [math]\displaystyle{ f(x)\,\! }[/math], the limits will vary based on the region over which the distribution is defined. For example, for the life distributions considered in this reference, with the exception of the normal distribution, this range would be [math]\displaystyle{ [0,+\infty ].\,\! }[/math]

Mathematical Relationship: pdf and cdf

The mathematical relationship between the pdf and cdf is given by:

[math]\displaystyle{ F(x)=\int_{0}^{x}f(s)ds \,\! }[/math]

where [math]\displaystyle{ s\,\! }[/math] is a dummy integration variable.

Conversely:

[math]\displaystyle{ f(x)=\frac{d(F(x))}{dx}\,\! }[/math]

The cdf is the area under the probability density function up to a value of [math]\displaystyle{ x\,\! }[/math]. The total area under the pdf is always equal to 1, or mathematically:

Total area under a pdf.
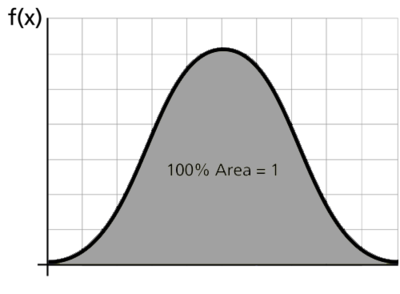
[math]\displaystyle{ \int_{-\infty}^{+\infty }f(x)dx=1\,\! }[/math]

The well-known normal (or Gaussian) distribution is an example of a probability density function. The pdf for this distribution is given by:

[math]\displaystyle{ f(t)=\frac{1}{\sigma \sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{t-\mu }{\sigma } \right)}^{2}}}}\,\! }[/math]

where [math]\displaystyle{ \mu \,\! }[/math] is the mean and [math]\displaystyle{ \sigma \,\! }[/math] is the standard deviation. The normal distribution has two parameters, [math]\displaystyle{ \mu \,\! }[/math] and [math]\displaystyle{ \sigma \,\! }[/math].

Another is the lognormal distribution, whose pdf is given by:

[math]\displaystyle{ f(t)=\frac{1}{t\cdot {{\sigma }^{\prime }}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{{t}^{\prime }}-{{\mu }^{\prime }}}{{{\sigma }^{\prime }}} \right)}^{2}}}}\,\! }[/math]

where [math]\displaystyle{ {\mu }'\,\! }[/math] is the mean of the natural logarithms of the times-to-failure and [math]\displaystyle{ {\sigma }'\,\! }[/math] is the standard deviation of the natural logarithms of the times-to-failure. Again, this is a 2-parameter distribution.

Reliability Function

The reliability function can be derived using the previous definition of the cumulative distribution function, [math]\displaystyle{ F(x)=\int_{0}^{x}f(s)ds \,\! }[/math]. From our definition of the cdf, the probability of an event occurring by time [math]\displaystyle{ t\,\! }[/math] is given by:

[math]\displaystyle{ F(t)=\int_{0}^{t}f(s)ds\ \,\! }[/math]

Or, one could equate this event to the probability of a unit failing by time [math]\displaystyle{ t\,\! }[/math].

Since this function defines the probability of failure by a certain time, we could consider this the unreliability function. Subtracting this probability from 1 will give us the reliability function, one of the most important functions in life data analysis. The reliability function gives the probability of success of a unit undertaking a mission of a given time duration. The following figure illustrates this.

Reliability as area under pdf.

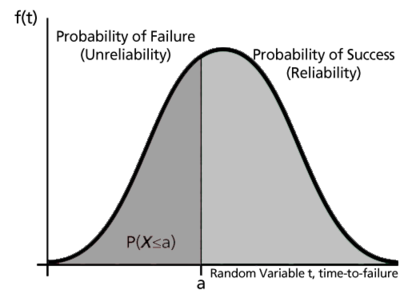
To show this mathematically, we first define the unreliability function, [math]\displaystyle{ Q(t)\,\! }[/math], which is the probability of failure, or the probability that our time-to-failure is in the region of 0 and [math]\displaystyle{ t\,\! }[/math]. This is the same as the cdf. So from [math]\displaystyle{ F(t)=\int_{0}^{t}f(s)ds\ \,\! }[/math]:

[math]\displaystyle{ Q(t)=F(t)=\int_{0}^{t}f(s)ds\,\! }[/math]

Reliability and unreliability are the only two events being considered and they are mutually exclusive; hence, the sum of these probabilities is equal to unity.

Then:

[math]\displaystyle{ \begin{align} Q(t)+R(t)= & 1 \\ R(t)= & 1-Q(t) \\ R(t)= & 1-\int_{0}^{t}f(s)ds \\ R(t)= & \int_{t}^{\infty }f(s)ds \end{align}\,\! }[/math]

Conversely:

[math]\displaystyle{ f(t)=-\frac{d(R(t))}{dt}\,\! }[/math]

Conditional Reliability Function

Conditional reliability is the probability of successfully completing another mission following the successful completion of a previous mission. The time of the previous mission and the time for the mission to be undertaken must be taken into account for conditional reliability calculations. The conditional reliability function is given by:

[math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)}\ \,\! }[/math]

Failure Rate Function

The failure rate function enables the determination of the number of failures occurring per unit time. Omitting the derivation, the failure rate is mathematically given as:

[math]\displaystyle{ \lambda (t)=\frac{f(t)}{R(t)}\ \,\! }[/math]

This gives the instantaneous failure rate, also known as the hazard function. It is useful in characterizing the failure behavior of a component, determining maintenance crew allocation, planning for spares provisioning, etc. Failure rate is denoted as failures per unit time.

Mean Life (MTTF)

The mean life function, which provides a measure of the average time of operation to failure, is given by:

[math]\displaystyle{ \overline{T}=m=\int_{0}^{\infty }t\cdot f(t)dt\,\! }[/math]

This is the expected or average time-to-failure and is denoted as the MTTF (Mean Time To Failure).

The MTTF, even though an index of reliability performance, does not give any information on the failure distribution of the component in question when dealing with most lifetime distributions. Because vastly different distributions can have identical means, it is unwise to use the MTTF as the sole measure of the reliability of a component.

Median Life

Median life, [math]\displaystyle{ \tilde{T}\,\! }[/math], is the value of the random variable that has exactly one-half of the area under the pdf to its left and one-half to its right. It represents the centroid of the distribution. The median is obtained by solving the following equation for [math]\displaystyle{ \breve{T}\,\! }[/math]. (For individual data, the median is the midpoint value.)

[math]\displaystyle{ \int_{-\infty}^{{\breve{T}}}f(t)dt=0.5\ \,\! }[/math]

Modal Life (or Mode)

The modal life (or mode), [math]\displaystyle{ \tilde{T}\,\! }[/math], is the value of [math]\displaystyle{ T\,\! }[/math] that satisfies:

[math]\displaystyle{ \frac{d\left[ f(t) \right]}{dt}=0\ \,\! }[/math]

For a continuous distribution, the mode is that value of [math]\displaystyle{ t\,\! }[/math] that corresponds to the maximum probability density (the value at which the pdf has its maximum value, or the peak of the curve).

Lifetime Distributions

A statistical distribution is fully described by its pdf. In the previous sections, we used the definition of the pdf to show how all other functions most commonly used in reliability engineering and life data analysis can be derived. The reliability function, failure rate function, mean time function, and median life function can be determined directly from the pdf definition, or [math]\displaystyle{ f(t)\,\! }[/math]. Different distributions exist, such as the normal (Gaussian), exponential, Weibull, etc., and each has a predefined form of [math]\displaystyle{ f(t)\,\! }[/math] that can be found in many references. In fact, there are certain references that are devoted exclusively to different types of statistical distributions. These distributions were formulated by statisticians, mathematicians and engineers to mathematically model or represent certain behavior. For example, the Weibull distribution was formulated by Waloddi Weibull and thus it bears his name. Some distributions tend to better represent life data and are most commonly called "lifetime distributions".

A more detailed introduction to this topic is presented in Life Distributions.

Retrieved from "https://www.reliawiki.com/index.php?title=Basic_Statistical_Background&oldid=28651"