Appendix B: Parameter Estimation
Once a life distribution and a life-stress relationship have been selected, the parameters (i.e. the variables that govern the characteristics of the ) need to be determined. Several parameter estimation methods, including probability plotting, least squares, and maximum likelihood, are available. This appendix will present an overview of these methods. Because the least squares method for analyzing accelerated life data is very limiting, it will be covered very briefly in this appendix. Interested readers can refer to Nelson [28] for a more detailed discussion of the least squares parameter estimation method.
Graphical Method
Graphical analysis is the simplest method for obtaining results in both life data and accelerated life testing analyses. Although they have limitations (presented later in this section), in general graphical methods are easily implemented and easy to interpret.
The graphical method for estimating the parameters of accelerated life data involves generating two types of plots. First, the life data at each individual stress level are plotted on a probability paper appropriate to the assumed life distribution (i.e. Weibull, exponential, or lognormal). The parameters of the distribution at each stress level are then estimated from the plot. Once these parameters have been estimated at each stress level, the second plot is created on a paper that linearizes the assumed life-stress relationship (i.e. Arrhenius, inverse power law, etc.). The parameters of the life-stress relationship are then estimated from the second plot. The life distribution and life-stress relationship are then combined to provide a single model that describes the accelerated life data. The next figure illustrates these two plots.
With this general understanding of the graphical parameter estimation method, we will continue with a more specific discussion of each step.
Life Distribution Parameters at Each Stress Level
The first step in the graphical analysis of accelerated data is to calculate the parameters of the assumed life distribution at each stress level. Because life data are collected at each test stress level in accelerated life tests, the assumed life distribution is fitted to data at each individual stress level. The parameters of the distribution at each stress level are then estimated using the probability plotting method described next.
Life Distribution Probability Plotting
The easiest parameter estimation method (to use by hand) for complex distributions such as the Weibull distribution is the method of probability plotting. Probability plotting involves a physical plot of the data on specially constructed probability plotting paper. This method is easily implemented by hand as long as one can obtain the appropriate probability plotting paper.
Probability plotting looks at the [math]\displaystyle{ cdf }[/math] (cumulative density function) of the distribution and attempts to linearize it by employing a specially constructed paper. For example, in the case of the 2-parameter Weibull distribution, the [math]\displaystyle{ cdf }[/math] and unreliability [math]\displaystyle{ Q(T) }[/math] can be shown to be:
- [math]\displaystyle{ F(T)=Q(T)=1-{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}} }[/math]
This function can then be linearized (i.e. put into the common form of [math]\displaystyle{ y=a+bx }[/math] ) as follows:
- [math]\displaystyle{ \begin{align} Q(T)=\ & 1-{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}} \\ \ln (1-Q(T))=\ & \ln \left( {{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}} \right) \\ \ln (1-Q(T))=\ & -{{\left( \frac{T}{\eta } \right)}^{\beta }} \\ \ln \left( -\ln (1-Q(T)) \right)=\ & \beta \ln \left( \frac{T}{\eta } \right) \end{align} }[/math]
- [math]\displaystyle{ \ln \left( \ln \left( \frac{1}{1-Q(T)} \right) \right)=\beta \ln \left( T \right)-\beta \ln \left( \eta \right) }[/math]
Then setting:
- [math]\displaystyle{ y=\ln \left( \ln \left( \frac{1}{1-Q(T)} \right) \right) }[/math]
and:
- [math]\displaystyle{ x=\ln \left( T \right) }[/math]
the equation can be rewritten as:
- [math]\displaystyle{ y=\beta x-\beta \ln \left( \eta \right) }[/math]
which is now a linear equation with a slope of [math]\displaystyle{ \beta }[/math] and an intercept of [math]\displaystyle{ \beta \ln \left( \eta \right). }[/math]
The next task is to construct a paper with the appropriate [math]\displaystyle{ x- }[/math] and [math]\displaystyle{ y-axes }[/math] . The [math]\displaystyle{ x-axis }[/math] is easy since it is simply logarithmic. The [math]\displaystyle{ y-axis, }[/math] however, must represent:
- [math]\displaystyle{ y=\ln \left( \ln \left( \frac{1}{1-Q(T)} \right) \right) }[/math]
where [math]\displaystyle{ Q(T) }[/math] is the unreliability. Such papers have been created by different vendors and are called Weibull probability plotting papers.
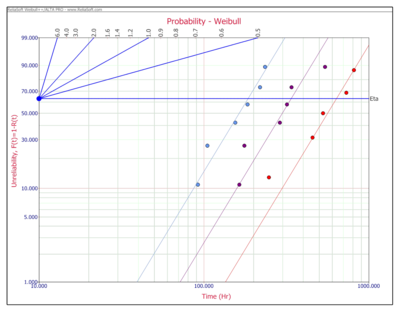
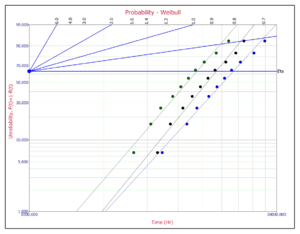
To illustrate, consider the following probability plot on a Weibull probability paper (created using Weibull++).
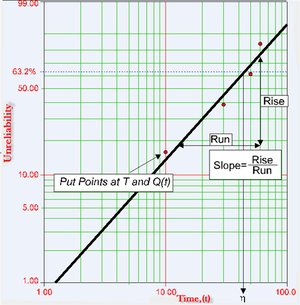
This paper is constructed based on the [math]\displaystyle{ y }[/math] and [math]\displaystyle{ x }[/math] transformation mentioned previously where the [math]\displaystyle{ y-axis }[/math] represents unreliability and the [math]\displaystyle{ x-axis }[/math] represents time. Both of these values must be known for each point (or time-to-failure) we want to plot.
Then, given the [math]\displaystyle{ y }[/math] and [math]\displaystyle{ x }[/math] value for each point, the points can easily be placed on the plot. Once the points are placed on the plot, the best possible straight line is drawn through these points. Once the line is drawn, the slope of the line can be obtained (most probability papers include a slope indicator to facilitate this) and thus the parameter [math]\displaystyle{ \beta , }[/math] which is the value of the slope, can be obtained.
To determine the scale parameter, [math]\displaystyle{ \eta }[/math] (also called the characteristic life by some authors), a little more work is required. Note that from before:
- [math]\displaystyle{ Q(T)=1-{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}} }[/math]
so at [math]\displaystyle{ T=\eta \ \ : }[/math]
- [math]\displaystyle{ \begin{align} & Q(T)= & 1-{{e}^{-{{\left( \tfrac{\eta }{\eta } \right)}^{\beta }}}} =\ & 1-{{e}^{-1}} = 0.632 =\ 63.2% \end{align} }[/math]
Thus if we entered the [math]\displaystyle{ y }[/math] axis at [math]\displaystyle{ Q(T)=63.2%, }[/math] the corresponding value of [math]\displaystyle{ T }[/math] will be equal to [math]\displaystyle{ \eta . }[/math] Using this simple but rather time consuming methodology, then, the parameters of the Weibull distribution can be determined. For data obtained from accelerated tests, this procedure is repeated for each stress level.
Determining the X and Y Position of the Plot Points
The points plotted on the probability plot represent our data, or more specifically in life data analysis, times-to-failure data. So if we tested four units that failed at 10, 20, 30 and 40 hours at a given stress level, we would use these times as our [math]\displaystyle{ x }[/math] values or time values. Determining the appropriate [math]\displaystyle{ y }[/math] plotting position, or the unreliability, is a little more complex. To determine the [math]\displaystyle{ y }[/math] plotting positions, we must first determine a value called the median rank for each failure.
Median Ranks
Median ranks are used to obtain an estimate of the unreliability, [math]\displaystyle{ Q({{T}_{j}}), }[/math] for each failure. It represents the value that the true probability of failure, [math]\displaystyle{ Q({{T}_{j}}), }[/math] should have at the [math]\displaystyle{ {{j}^{th}} }[/math] failure out of a sample of [math]\displaystyle{ N }[/math] units, at a [math]\displaystyle{ 50% }[/math] confidence level. (Confidence intervals are presented in detail in Appendix A of this reference.) This is an estimate of the value based on the binomial distribution.
The rank can be found for any percentage point, [math]\displaystyle{ P }[/math] , greater than zero and less than one, by solving the cumulative binomial distribution for [math]\displaystyle{ Z }[/math] (rank for the [math]\displaystyle{ {{j}^{th}} }[/math] failure) [31]:
- [math]\displaystyle{ P=\underset{k=j}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} N \\ k \\ \end{matrix} \right){{Z}^{k}}{{\left( 1-Z \right)}^{N-k}} }[/math]
where [math]\displaystyle{ N }[/math] is the sample size and [math]\displaystyle{ j }[/math] the order number.
The median rank is obtained by solving the following equation for [math]\displaystyle{ Z }[/math] :
- [math]\displaystyle{ 0.50=\underset{k=j}{\overset{N}{\mathop \sum }}\,\left( \begin{matrix} N \\ k \\ \end{matrix} \right){{Z}^{k}}{{\left( 1-Z \right)}^{N-k}} }[/math]
For example, if [math]\displaystyle{ N=4 }[/math] and we have four failures at that particular stress level, we would solve the median rank equation four times - once for each failure with [math]\displaystyle{ j= }[/math] 1, 2, 3, and 4 - for the value of [math]\displaystyle{ Z. }[/math] This result can then be used as the unreliability for each failure, or the [math]\displaystyle{ y }[/math] plotting position. Solution of the above equation requires numerical methods.
A more straightforward and easier method of estimating median ranks is to apply two transformations to the above equation, first to the beta distribution and then to the F distribution, resulting in [31]:
- [math]\displaystyle{ \begin{align} MR =\ & \tfrac{1}{1+\tfrac{N-j+1}{j}{{F}_{0.50;m;n}}}, \\ m =\ & 2(N-j+1), \\ n =\ & 2j. \\ \end{align} }[/math]
[math]\displaystyle{ {{F}_{0.50;m;n}} }[/math] denotes the F distribution at the 0.50 point, with [math]\displaystyle{ m }[/math] and [math]\displaystyle{ n }[/math] degrees of freedom, for the [math]\displaystyle{ {{j}^{th}} }[/math] failure out of units.
A quick but less accurate approximation of the median ranks is also given by [31]:
- [math]\displaystyle{ MR=\frac{j-0.3}{N+0.4} }[/math]
This approximation of the median ranks is also known as Benard's approximation.
Some Shortfalls of Manual Probability Plotting
Besides the most obvious shortfall of probability plotting, the amount of effort required, manual probability plotting is not always consistent in the results. Two people plotting a straight line through a set of points will not always draw this line the same way and they will therefore come up with slightly different results. In addition, when dealing with accelerated test data a probability plot must be constructed for each stress level. This implies that sufficient failures must be observed at each stress level, which is not always possible.
Probability Plotting with Censored Data
Probability plotting can also be performed with censored data. The methodology involved is rather laborious. ReliaSoft [31] presents this methodology.
Least Squares Method
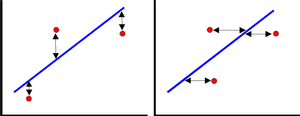
The least squares parameter estimation method is a variation of the probability plotting methodology in which one mathematically fits a straight line to a set of points in an attempt to estimate the parameters. The method of least squares requires that a straight line be fitted to a set of data points such that the sum of the squares of the vertical deviations from the points to the line is minimized, if the regression is on Y, or that the line be fitted to a set of data points such that the sum of the squares of the horizontal deviations from the points to the line is minimized, if the regression is on X.
The regression on Y is not necessarily the same as the regression on X. The only time when the two regressions are the same (i.e. will yield the same equation for a line) is when the data lie perfectly on a line. ReliaSoft [31] presents this methodology in detail.
Life-Stress Relationship Plotting
Once the parameters of the life distribution have been obtained using probability plotting methods, a second plot is created in which life is plotted versus stress. To do this, a life characteristic must be chosen to be plotted. The life characteristic can be any percentile, such as [math]\displaystyle{ B(x) }[/math] life, the scale parameter, mean life, etc. The plotting paper used is a special type of paper that linearizes the life-stress relationship. For example, a log-log paper linearizes the inverse power law relationship, and a log-reciprocal paper linearizes the Arrhenius relationship. The parameters of the model are then estimated by solving for the slope and the intercept of the line. This methodology is illustrated in Example 1.
Example 1
Consider the following times-to-failure data at three different stress levels.
| Stress | 393 psi | 408 psi | 423 psi |
| Time Failed (hrs) | 3450 | 3300 | 2645 |
| 4340 | 3720 | 3100 | |
| 4760 | 4180 | 3400 | |
| 5320 | 4560 | 3800 | |
| 5740 | 4920 | 4100 | |
| 6160 | 5280 | 4400 | |
| 6580 | 5640 | 4700 | |
| 7140 | 6233 | 5100 | |
| 8101 | 6840 | 5700 | |
| 8960 | 7380 | 6400 |
Estimate the parameters for a Weibull assumed life distribution and for the inverse power law life-stress relationship.
Solution
First the parameters of the Weibull distribution need to be determined. The data are individually analyzed (for each stress level) using the probability plotting method, or software such as ReliaSoft's Weibull++, with the following results:
- [math]\displaystyle{ \begin{align} & [{{\widehat{\beta }}_{1}}= & 3.8,\text{ }{{\widehat{\eta }}_{1}}=6692] \\ & \text{ }\!\![\!\!\text{ }{{\widehat{\beta }}_{2}}= & 4.2,\text{ }{{\widehat{\eta }}_{2}}=5716] \\ & [{{\widehat{\beta }}_{3}}= & 4,\text{ }{{\widehat{\eta }}_{3}}=4774] \end{align} }[/math]
where:
• [math]\displaystyle{ {{\widehat{\beta }}_{1}}, }[/math] [math]\displaystyle{ {{\widehat{\eta }}_{1}} }[/math] are the parameters of the 393 psi data.
• [math]\displaystyle{ {{\widehat{\beta }}_{2}}, }[/math] [math]\displaystyle{ {{\widehat{\eta }}_{2}} }[/math] are the parameters of the 408 psi data.
• [math]\displaystyle{ {{\widehat{\beta }}_{3}}, }[/math] [math]\displaystyle{ {{\widehat{\eta }}_{3}} }[/math] are the parameters of the 423 psi data.
Since the shape parameter, [math]\displaystyle{ \beta , }[/math] is not common for the three stress levels, the average value is estimated.
- [math]\displaystyle{ {{\widehat{\beta }}_{common}}=4 }[/math]
Averaging the [math]\displaystyle{ betas }[/math] is one of many simple approaches available. One can also use a weighted average, since the uncertainty on beta is greater for smaller sample sizes. In most practical applications the value of [math]\displaystyle{ \widehat{\beta } }[/math] will vary (even though it is assumed constant) due to sampling error, etc. The variability in the value of [math]\displaystyle{ \widehat{\beta } }[/math] is a source of error when performing analysis by averaging the [math]\displaystyle{ betas }[/math] . MLE analysis, which uses a common [math]\displaystyle{ \widehat{\beta } }[/math] , is not susceptible to this error. MLE analysis is the method of parameter estimation used in ALTA and it is explained in the next section.
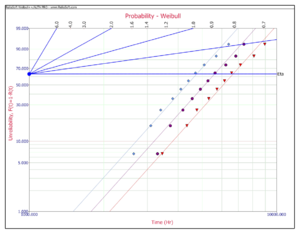
Redraw each line with a [math]\displaystyle{ \widehat{\beta }=4, }[/math] and estimate the new [math]\displaystyle{ etas, }[/math] as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\eta }}_{1}}= & 6650 \\ & {{\widehat{\eta }}_{2}}= & 5745 \\ & {{\widehat{\eta }}_{3}}= & 4774 \end{align} }[/math]
The IPL relationship is given by:
- [math]\displaystyle{ L(V)=\frac{1}{K{{V}^{n}}} }[/math]
where:
[math]\displaystyle{ L }[/math] represents a quantifiable life measure ( [math]\displaystyle{ \eta }[/math] in the Weibull case), [math]\displaystyle{ V }[/math] represents the stress level, [math]\displaystyle{ K }[/math] is one of the parameters, and [math]\displaystyle{ n }[/math] is another model parameter. The relationship is linearized by taking the logarithm of both sides which yields:
- [math]\displaystyle{ \ln (L)=-\ln K-n\ln V }[/math]
where [math]\displaystyle{ L=\eta }[/math] , (- [math]\displaystyle{ \ln K) }[/math] is the intercept, and (- [math]\displaystyle{ n) }[/math] is the slope of the line.
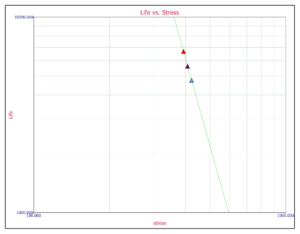
The values of [math]\displaystyle{ \eta }[/math] obtained previously are now plotted on a log-linear scale yielding the following plot:
The slope of the line is the [math]\displaystyle{ n }[/math] parameter, which is obtained from the plot:
- [math]\displaystyle{ \begin{align} & Slope=\ \frac{\ln ({{T}_{2}})-\ln ({{T}_{1}})}{\ln ({{V}_{2}})-\ln ({{V}_{1}})} =\ \frac{\ln (10,000)-\ln (6,000)}{\ln (360)-\ln (403)} =\ -4.5272 \end{align} }[/math]
Thus:
- [math]\displaystyle{ \widehat{n}=4.5272 }[/math]
Solving the inverse power law equation with respect to [math]\displaystyle{ K }[/math] yields:
- [math]\displaystyle{ \widehat{K}=\frac{1}{L{{V}^{n}}} }[/math]
Substituting V=403, the corresponding L (from the plot), L=6,000 and the previously estimated [math]\displaystyle{ n\ \ : }[/math]
- [math]\displaystyle{ \begin{align} & \widehat{K}=\ \frac{1}{6000\text{ }{{403}^{4.5272}}} =\ 2.67\cdot {{10}^{-16}} \end{align} }[/math]
Comments on the Graphical Method
Although the graphical method is simple, it is quite laborious. Furthermore, many issues surrounding its use require careful consideration. Some of these issues are presented next:
• What happens when no failures are observed at one or more stress level? In this case, plotting methods cannot be employed. Discarding the data would be a mistake since every piece of life data information is important.
• In the step at which the life-stress relationship is linearized and plotted to obtain its parameters, you must be able to linearize the function, which is not always possible.
• In real accelerated tests the data sets are small. Separating them and individually plotting them, and then subsequently replotting the results, increases the underlying error.
• During initial parameter estimation, the parameter that is assumed constant will more than likely vary. What value do you use?
• Confidence intervals on all of the results cannot be ascertained using graphical methods.
The maximum likelihood estimation parameter estimation method described next overcomes these shortfalls, and is the method utilized in ALTA.
MLE (Maximum Likelihood) Parameter Estimation
The idea behind maximum likelihood parameter estimation is to determine the parameters that maximize the probability (likelihood) of the sample data. From a statistical point of view, the method of maximum likelihood is considered to be more robust (with some exceptions) and yields estimators with good statistical properties. In other words, MLE methods are versatile and apply to most models and to different types of data. In addition, they provide efficient methods for quantifying uncertainty through confidence bounds. Although the methodology for maximum likelihood estimation is simple, the implementation is mathematically intense. Using today's computer power, however, mathematical complexity is not a big obstacle. The MLE methodology is presented next.
Background Theory
This section presents the theory that underlies maximum likelihood estimation for complete data.
If [math]\displaystyle{ x }[/math] is a continuous random variable with [math]\displaystyle{ pdf }[/math] :
- [math]\displaystyle{ f(x;{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) }[/math]
where [math]\displaystyle{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}} }[/math] are [math]\displaystyle{ k }[/math] unknown constant parameters which need to be estimated, conduct an experiment and obtain [math]\displaystyle{ N }[/math] independent observations, [math]\displaystyle{ {{x}_{1}},{{x}_{2}}, }[/math] ..., [math]\displaystyle{ {{x}_{N}} }[/math] . Then the likelihood function is given by the following product:
- [math]\displaystyle{ L({{x}_{1}},{{x}_{2}},...,{{x}_{N}}|{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})=L=\underset{i=1}{\overset{N}{\mathop \prod }}\,f({{x}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) }[/math]
- [math]\displaystyle{ i=1,2,...,N }[/math]
The logarithmic likelihood function is given by:
- [math]\displaystyle{ \Lambda =\ln L=\underset{i=1}{\overset{N}{\mathop \sum }}\,\ln f({{x}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) }[/math]
The maximum likelihood estimators (MLE) of [math]\displaystyle{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}, }[/math] are obtained by maximizing [math]\displaystyle{ L }[/math] or [math]\displaystyle{ \Lambda . }[/math]
By maximizing [math]\displaystyle{ \Lambda , }[/math] which is much easier to work with than [math]\displaystyle{ L }[/math] , the maximum likelihood estimators (MLE) of [math]\displaystyle{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}} }[/math] are the simultaneous solutions of k equations such that:
- [math]\displaystyle{ \frac{\partial (\Lambda )}{\partial {{\theta }_{j}}}=0,j=1,2,...,k }[/math]
Even though it is common practice to plot the MLE solutions using median ranks (points are plotted according to median ranks and the line according to the MLE solutions), this is not completely accurate. As it can be seen from the equations above, the MLE method is independent of any kind of ranks or plotting methods. For this reason, many times the MLE solution appears not to track the data on the probability plot. This is perfectly acceptable since the two methods are independent of each other and in no way suggests that the solution is wrong.
Illustrating the MLE Method Using the Exponential Distribution
• To estimate [math]\displaystyle{ \widehat{\lambda } }[/math] for a sample of [math]\displaystyle{ n }[/math] units (all tested to failure), first obtain the likelihood function:
- [math]\displaystyle{ \begin{align} & L(\lambda |{{t}_{1}},{{t}_{2}},...,{{t}_{n}})=\ \underset{i=1}{\overset{n}{\mathop \prod }}\,f({{t}_{i}}) =\ \underset{i=1}{\overset{n}{\mathop \prod }}\,\lambda {{e}^{-\lambda {{t}_{i}}}} =\ {{\lambda }^{n}}\cdot {{e}^{-\lambda \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{t}_{i}}}} \end{align} }[/math]
• Take the natural log of both sides:
- [math]\displaystyle{ \Lambda =\ln (L)=n\ln (\lambda )-\lambda \underset{i=1}{\overset{n}{\mathop \sum }}\,{{t}_{i}} }[/math]
• Obtain [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \lambda } }[/math] and set it equal to zero:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-\underset{i=1}{\overset{n}{\mathop \sum }}\,{{t}_{i}}=0 }[/math]
• Solve for [math]\displaystyle{ \widehat{\lambda } }[/math] or:
- [math]\displaystyle{ \hat{\lambda }=\frac{n}{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{t}_{i}}} }[/math]
Notes on [math]\displaystyle{ \lambda }[/math]
• Note that the value of [math]\displaystyle{ \lambda }[/math] is an estimate because if we obtain another sample from the same population and re-estimate [math]\displaystyle{ \lambda }[/math] , the new value would differ from the one previously calculated.
• In plain language, [math]\displaystyle{ \hat{\lambda } }[/math] is an estimate of the true value of [math]\displaystyle{ \lambda }[/math] .
• How close is the value of our estimate to the true value? To answer this question, one must first determine the distribution of the parameter, in this case [math]\displaystyle{ \lambda }[/math] . This methodology introduces a new term, confidence interval, which allows us to specify a range for our estimate with a certain confidence level. The treatment of confidence intervals is integral to reliability engineering, and to all of statistics. (Confidence intervals are presented in Appendix A.)
Illustrating the MLE Method Using the Normal Distribution
To obtain the MLE estimates for the mean, [math]\displaystyle{ \bar{T}, }[/math] and standard deviation, [math]\displaystyle{ {{\sigma }_{T}}, }[/math] for the normal distribution, start with the [math]\displaystyle{ pdf }[/math] of the normal distribution, which is given by:
- [math]\displaystyle{ f(T)=\frac{1}{{{\sigma }_{T}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{T-\bar{T}}{{{\sigma }_{T}}} \right)}^{2}}}} }[/math]
If [math]\displaystyle{ {{T}_{1}},{{T}_{2}},...,{{T}_{N}} }[/math] are known times-to-failure (and with no suspensions), then the likelihood function is given by:
- [math]\displaystyle{ L({{T}_{1}},{{T}_{2}},...,{{T}_{N}}|\bar{T},{{\sigma }_{T}})=L=\underset{i=1}{\overset{N}{\mathop \prod }}\,\left[ \frac{1}{{{\sigma }_{T}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{{T}_{i}}-\bar{T}}{{{\sigma }_{T}}} \right)}^{2}}}} \right] }[/math]
- [math]\displaystyle{ L=\frac{1}{{{({{\sigma }_{T}}\sqrt{2\pi })}^{N}}}{{e}^{-\tfrac{1}{2}\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{\left( \tfrac{{{T}_{i}}-\bar{T}}{{{\sigma }_{T}}} \right)}^{2}}}} }[/math]
then:
- [math]\displaystyle{ \Lambda =\ln L=-\frac{N}{2}\ln (2\pi )-N\ln {{\sigma }_{T}}-\frac{1}{2}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( \frac{{{T}_{i}}-\bar{T}}{{{\sigma }_{T}}} \right)}^{2}} }[/math]
Then taking the partial derivatives of [math]\displaystyle{ \Lambda }[/math] with respect to each one of the parameters and setting it equal to zero yields:
- [math]\displaystyle{ \frac{\partial (\Lambda )}{\partial \bar{T}}=\frac{1}{\sigma _{T}^{2}}\underset{i=1}{\overset{N}{\mathop \sum }}\,({{T}_{i}}-\bar{T})=0 }[/math]
and:
- [math]\displaystyle{ \frac{\partial (\Lambda )}{\partial {{\sigma }_{T}}}=-\frac{N}{{{\sigma }_{T}}}+\frac{1}{\sigma _{T}^{3}}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}}=0 }[/math]
Solving the above equations simultaneously yields:
- [math]\displaystyle{ \bar{T}=\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{T}_{i}} }[/math]
and:
- [math]\displaystyle{ \begin{align} & \hat{\sigma }_{T}^{2}= & \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}} \\ & & \\ & {{{\hat{\sigma }}}_{T}}= & \sqrt{\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}}} \end{align} }[/math]
These solutions are only valid for data with no suspensions, i.e. all units are tested to failure. In cases in which suspensions are present, the methodology changes and the problem becomes much more complicated.
Estimators
As mentioned above, the parameters obtained from maximizing the likelihood function are estimators of the true value. It is clear that the sample size determines the accuracy of an estimator. If the sample size equals the whole population, then the estimator is the true value. Estimators have properties such as unbiasedness, sufficiency, consistency, and efficiency. Numerous books and papers deal with these properties and this coverage is beyond the scope of this reference. However, we would like to briefly address unbiasedness and consistency.
Unbiased Estimators
An estimator is said to be unbiased if and only if the estimator [math]\displaystyle{ \widehat{\theta }=d({{X}_{1,}}{{X}_{2,}} }[/math] [math]\displaystyle{ ...,{{X}_{n)}} }[/math] satisfies the condition [math]\displaystyle{ E\left[ \widehat{\theta } \right] }[/math] [math]\displaystyle{ =\theta }[/math] for all [math]\displaystyle{ \theta \in \Omega . }[/math] Note that [math]\displaystyle{ E\left[ X \right] }[/math] denotes the expected value of X and is defined by (for continuous distributions):
- [math]\displaystyle{ \begin{align} E\left[ X \right]=\ & \int_{\varpi }x\cdot f(x)dx \\ X\in \ & \varpi \end{align} }[/math]
This implies that the true value is not consistently underestimated nor overestimated by an unbiased estimator.
Consistent Estimators
An unbiased estimator that converges more closely to the true value as the sample size increases is called a consistent estimator. In the example above, the standard deviation of the normal distribution was obtained using MLE. This estimator of the true standard deviation is a biased one. It can be shown [4] that the consistent estimate of the variance and standard deviation for complete data (for the normal and lognormal distribution) is given by:
- [math]\displaystyle{ \begin{align} & \hat{\sigma }_{T}^{2}= & \left[ \frac{N}{N-1} \right]\cdot \left[ \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}} \right]=\frac{1}{N-1}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}} \\ & {{{\hat{\sigma }}}_{T}}= & \sqrt{\left[ \frac{N}{N-1} \right]\cdot \left[ \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}} \right]}=\sqrt{\frac{1}{N-1}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}}} \end{align} }[/math]
Note that for larger values of N, [math]\displaystyle{ \sqrt{\left[ N/(N-1) \right]} }[/math] tends to 1.
MLE of Accelerated Life Data
Maximum likelihood offers a very powerful method in estimating the parameters of accelerated testing models, making possible the analysis of very complex models. In the beginning of this appendix, a graphical method for obtaining the parameters of accelerated testing models was illustrated. It involved estimating the parameters of the life distribution separately for each individual stress level, and then plotting the life-stress relationship in a linear manner on a separate life vs. stress plot. In other words, the life distribution and the life-stress relationship were treated separately. However, using the MLE method, the life distribution and the life-stress relationship can be treated as ONE complete model which describes both. This can be accomplished by including the life-stress relationship into the [math]\displaystyle{ pdf }[/math] of the life distribution.
Background Theory
The maximum likelihood for accelerated life testing analysis is formulated in the same way as shown previously. However, in this case the stress level of each individual observation is included in the likelihood function. Consider a continuous random variable [math]\displaystyle{ x(v), }[/math] where [math]\displaystyle{ v }[/math] is the stress. The [math]\displaystyle{ pdf }[/math] of the random variable now becomes a function of both [math]\displaystyle{ x }[/math] and [math]\displaystyle{ v }[/math] :
- [math]\displaystyle{ f(x,v;{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) }[/math]
where [math]\displaystyle{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}} }[/math] are [math]\displaystyle{ k }[/math] unknown constant parameters which need to be estimated. Conduct an experiment and obtain [math]\displaystyle{ N }[/math] independent observations, [math]\displaystyle{ {{x}_{1}},{{x}_{2}},...,{{x}_{N}} }[/math] each at a corresponding stress, [math]\displaystyle{ {{v}_{1}}, }[/math] [math]\displaystyle{ {{v}_{2}},..., }[/math] [math]\displaystyle{ {{v}_{N}} }[/math] . Then the likelihood function for complete data is given by:
- [math]\displaystyle{ L(({{x}_{1}},\text{ }{{v}_{1}}),({{x}_{2}},\text{ }{{v}_{2}}),...,({{x}_{N}},\text{ }{{v}_{N}})|{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})=\underset{i=1}{\overset{N}{\mathop \prod }}\,f({{x}_{i}},{{v}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) }[/math]
- [math]\displaystyle{ i=1,2,...,N }[/math]
The logarithmic likelihood function is given by:
- [math]\displaystyle{ \Lambda =\ln L=\underset{i=1}{\overset{N}{\mathop \sum }}\,\ln f({{x}_{i}},{{v}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) }[/math]
The maximum likelihood estimators (MLE) of [math]\displaystyle{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}, }[/math] are obtained by maximizing [math]\displaystyle{ L }[/math] or [math]\displaystyle{ \Lambda . }[/math]
In this case, [math]\displaystyle{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}} }[/math] are the parameters of the combined model which includes the parameters of the life distribution and the parameters of the life-stress relationship. Note that in the above equations, [math]\displaystyle{ N }[/math] is the total number of observations. This means that the sample size is no longer broken into the number of observations at each stress level. In Example 1, the sample size at the stress level of 20V was 4, and 15 at 36V. Using the above equations, however, the test's sample size is 19.
Once the parameters are estimated, they can be substituted back into the life distribution and the life-stress relationship.
Example 2
The following example illustrates the use of the MLE method on accelerated life test data. Consider the inverse power law relationship, given by:
- [math]\displaystyle{ L(V)=\frac{1}{K{{V}^{n}}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, [math]\displaystyle{ V }[/math] represents the stress level, [math]\displaystyle{ K }[/math] is one of the parameters, and [math]\displaystyle{ n }[/math] is another model parameter.
Assume that the life at each stress follows a Weibull distribution, with a [math]\displaystyle{ pdf }[/math] given by:
- [math]\displaystyle{ f(t)=\frac{\beta }{\eta }{{\left( \frac{T}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}} }[/math]
where the time-to-failure, [math]\displaystyle{ t }[/math] , is a function of stress, [math]\displaystyle{ V }[/math] .
A common life measure needs to determined so that it can be easily included in the Weibull [math]\displaystyle{ pdf }[/math]. In this case, setting [math]\displaystyle{ \eta =L(V) }[/math] (which is the life at 63.2%) and substituting in the Weibull [math]\displaystyle{ pdf }[/math], yields the following IPL-Weibull [math]\displaystyle{ pdf }[/math] :
- [math]\displaystyle{ f(t,V)=\beta K{{V}^{n}}{{\left( K{{V}^{n}}T \right)}^{\beta -1}}{{e}^{-{{\left( K{{V}^{n}}T \right)}^{\beta }}}} }[/math]
The log-likelihood function for the complete data is given by:
Note that [math]\displaystyle{ \beta }[/math] is now the common shape parameter to solve for, along with [math]\displaystyle{ K }[/math] and [math]\displaystyle{ n. }[/math]
Analysis of Censored Data
So far we have discussed parameter estimation methods for complete data only. We will expand on that approach in this section by including the maximum likelihood estimation method for right censored data. The method is based on the same principles covered previously but modified to take into account the fact that some of the data is censored.
MLE Analysis Of Right Censored Data
The maximum likelihood method is, at this point, by far the most appropriate analysis method for censored data. It is versatile and applicable to most accelerated life testing models. When performing maximum likelihood analysis, the likelihood function needs to be expanded to take into account the suspended items. A big advantage of using MLE when dealing with censored data is that each suspension term is included in the likelihood function. Thus, the estimates of the parameters are obtained from consideration of the entire population. Using MLE properties, confidence bounds can be obtained which also account for all the suspension terms. In the case of suspensions and where [math]\displaystyle{ x }[/math] is a continuous random variable with [math]\displaystyle{ pdf }[/math] and [math]\displaystyle{ cdf : }[/math]
- [math]\displaystyle{ \begin{align} & & \ \ \ f(x;\,{{\theta }_{1}},\,{{\theta }_{2}},...,\,{{\theta }_{k}}) \\ & & \ \ \ F(x;\,{{\theta }_{1}},\,{{\theta }_{2}},...,\,{{\theta }_{k}}) \end{align} }[/math]
where [math]\displaystyle{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}} }[/math] are the [math]\displaystyle{ k }[/math] unknown parameters which need to be estimated from [math]\displaystyle{ R }[/math] observed failures at [math]\displaystyle{ \left( {{T}_{1}},{{V}_{1}} \right),({{T}_{2}},{{V}_{2}})...({{T}_{R}},{{V}_{R}}), }[/math] and [math]\displaystyle{ M }[/math] observed suspensions at [math]\displaystyle{ \left( {{S}_{1}},V{{s}_{1}} \right),({{S}_{2}},V{{s}_{2}})...({{S}_{M}},V{{s}_{M}}), }[/math] where [math]\displaystyle{ {{V}_{R}} }[/math] is the [math]\displaystyle{ {{R}^{th}} }[/math] stress level corresponding to the [math]\displaystyle{ {{R}^{th}} }[/math] observed failure, and [math]\displaystyle{ V{{s}_{M}} }[/math] is the [math]\displaystyle{ {{M}^{th}} }[/math] stress level corresponding to the [math]\displaystyle{ {{M}^{th}} }[/math] observed suspension. The likelihood function is then formulated as follows:
- [math]\displaystyle{ \begin{align} & L(\left( {{T}_{1}},{{V}_{1}} \right),({{T}_{2}},{{V}_{2}}) \\ & ...,({{T}_{R}},{{V}_{R}}),\left( {{S}_{1}},V{{s}_{1}} \right),({{S}_{2}},V{{s}_{2}}) \\ & ...,({{S}_{M}},V{{s}_{M}})|{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) \\ & = \underset{i=1}{\overset{R}{\mathop \prod }}\,f({{T}_{i}},{{V}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})\cdot \underset{j=1}{\overset{M}{\mathop \prod }}\,[1-F({{S}_{j}},V{{s}_{j}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})] \end{align} }[/math]
and the parameters are solved by maximizing this equation. In most cases, no closed form solution exists for this maximum, or for the parameters.
Example 3
Example 1 was repeated using MLE with the following results:
- [math]\displaystyle{ \begin{align} \widehat{\beta }=\ & 4.30218250 \\ \widehat{K}=\ & 1.61781534E-16 \\ \widehat{n}=\ & 4.61145743 \end{align} }[/math]
In the individual analysis (probability plotting) the [math]\displaystyle{ betas }[/math] were averaged in order to estimate a common shape parameter. This introduced further uncertainties into the analysis. However, in this case (using MLE) the parameter [math]\displaystyle{ \beta }[/math] was estimated from the entire data set.
Conclusions
In this appendix, two methods for estimating the parameters of accelerated life testing models were presented. First, the graphical method was illustrated using a probability plotting method for obtaining the parameters of the life distribution. The parameters of the life-stress relationship were then estimated graphically by linearizing the model. However, not all life-stress relationships can be linearized. In addition, estimating the parameters of each individual distribution leads to an accumulation of uncertainties, depending on the number of failures and suspensions observed at each stress level. Furthermore, the slopes (shape parameters) of each individual distribution are rarely equal (common). Using the graphical method, one must estimate a common shape parameter (usually the average) and repeat the analysis. By doing so, further uncertainties are introduced on the estimates, and these are uncertainties that cannot be quantified. The second method, the Maximum Likelihood Estimation, treated both the life distribution and the life-stress relationship as one model, the parameters of that model can be estimated using the complete likelihood function. Doing so, a common shape parameter is estimated for the model, thus eliminating the uncertainties of averaging the individual shape parameters. All uncertainties are accounted for in the form of confidence bounds (presented in detail in Appendix A), which are quantifiable because they are obtained based on the overall model.