Appendix B: Parameter Estimation: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
 
(37 intermediate revisions by 5 users not shown)
Line 1: Line 1:
{{template:ALTABOOK SUB|Appendix B|Parameter Estimation}}
{{template:ALTABOOK|Appendix B|Parameter Estimation}}
   
   
This appendix presents two methods for estimating the parameters of accelerated life test data analysis models (ALTA models). The graphical method, which is based on probability plotting or least squares (Rank Regression on X or Rank Regression on Y), has some limitations. Therefore, the Maximum Likelihood Estimation (MLE) method is used for all parameter estimation in ALTA.  
This appendix presents two methods for estimating the parameters of accelerated life test data analysis models (ALTA models). The graphical method, which is based on probability plotting or least squares (Rank Regression on X or Rank Regression on Y), has some limitations. Therefore, the Maximum Likelihood Estimation (MLE) method is used for all parameter estimation in ALTA.  
Line 6: Line 6:
The graphical method for estimating the parameters of accelerated life data involves generating two types of plots. First, the life data at each individual stress level are plotted on a probability paper appropriate to the assumed life distribution (i.e., Weibull, exponential, or lognormal). This can be done using either [[Parameter_Estimation#Probability_Plotting|Probability Plotting]] or [[Parameter_Estimation#Least_Squares_Parameter_Estimation|Least Squares (Rank Regression)]].  
The graphical method for estimating the parameters of accelerated life data involves generating two types of plots. First, the life data at each individual stress level are plotted on a probability paper appropriate to the assumed life distribution (i.e., Weibull, exponential, or lognormal). This can be done using either [[Parameter_Estimation#Probability_Plotting|Probability Plotting]] or [[Parameter_Estimation#Least_Squares_Parameter_Estimation|Least Squares (Rank Regression)]].  


The parameters of the distribution at each stress level are then estimated from the plot. Once these parameters have been estimated at each stress level, the second plot is created on a paper that linearizes the assumed life-stress relationship (e.g., Arrhenius, inverse power law, etc.). To do this, a life characteristic must be chosen to be plotted. The life characteristic can be any percentile, such as BX% life, the scale parameter, mean life, etc. The plotting paper used is a special type of paper that linearizes the life-stress relationship. For example, a log-log paper linearizes the inverse power law relationship, and a log-reciprocal paper linearizes the Arrhenius relationship. The parameters of the model are then estimated by solving for the slope and the intercept of the line.


The parameters of the distribution at each stress level are then estimated from the plot. Once these parameters have been estimated at each stress level, the second plot is created on a paper that linearizes the assumed life-stress relationship (e.g., Arrhenius, inverse power law, etc.). To do this, a life characteristic must be chosen to be plotted. The life characteristic can be any percentile, such as B(x) life, the scale parameter, mean life, etc. The plotting paper used is a special type of paper that linearizes the life-stress relationship. For example, a log-log paper linearizes the inverse power law relationship, and a log-reciprocal paper linearizes the Arrhenius relationship. The parameters of the model are then estimated by solving for the slope and the intercept of the line. 
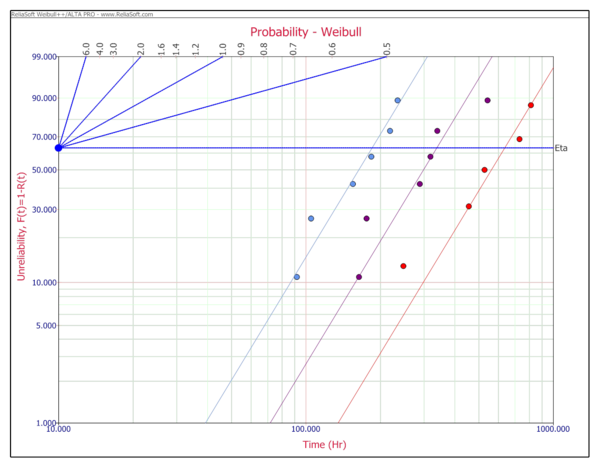
[[Image:ALTAB.1.png|center|600px]]
 
[[Image:ALTAB.1.1.png|center|600px]]
 
[[Image:ALTAB.1.png|center|650px|]]
 


==Example of Graphical Method for Accelerated Life Data==
==Example of Graphical Method for Accelerated Life Data==
<br>
Consider the following times-to-failure data at three different stress levels.
Consider the following times-to-failure data at three different stress levels.
{|align="center" border="1" style="bordercollapse:collapse;"
{|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5"
|-
|-
|Stress||393 psi|| 408 psi|| 423 psi
|Stress||393 psi|| 408 psi|| 423 psi
Line 41: Line 38:
|}
|}


Estimate the parameters for a Weibull assumed life distribution and for the inverse power law life-stress relationship.
'''Solution'''


Estimate the parameters for a Weibull assumed life distribution and for the inverse power law life-stress relationship.
<br>
<br>
===Solution===
First the parameters of the Weibull distribution need to be determined. The data are individually analyzed (for each stress level) using the probability plotting method, or software such as ReliaSoft's Weibull++, with the following results:
First the parameters of the Weibull distribution need to be determined. The data are individually analyzed (for each stress level) using the probability plotting method, or software such as ReliaSoft's Weibull++, with the following results:


::<math>\begin{align}
::<math>\begin{align}
   & [{{\widehat{\beta }}_{1}}= & 3.8,\text{ }{{\widehat{\eta }}_{1}}=6692] \\  
   & [{{\widehat{\beta }}_{1}}= & 3.8,\text{ }{{\widehat{\eta }}_{1}}=6692] \\  
  & \text{ }\!\![\!\!\text{ }{{\widehat{\beta }}_{2}}= & 4.2,\text{ }{{\widehat{\eta }}_{2}}=5716] \\  
  & \text{ }\!\![\!\!\text{ }{{\widehat{\beta }}_{2}}= & 4.2,\text{ }{{\widehat{\eta }}_{2}}=5716] \\  
  & [{{\widehat{\beta }}_{3}}= & 4,\text{ }{{\widehat{\eta }}_{3}}=4774]   
  & [{{\widehat{\beta }}_{3}}= & 4.0,\text{ }{{\widehat{\eta }}_{3}}=4774]   
\end{align}</math>
\end{align}\,\!</math>
 


where:
where:
<br>
• <math>{{\widehat{\beta }}_{1}},</math>  <math>{{\widehat{\eta }}_{1}}</math>  are the parameters of the 393 psi data.


• <math>{{\widehat{\beta }}_{2}},</math>   <math>{{\widehat{\eta }}_{2}}</math> are the parameters of the 408 psi data.
*<math>{{\widehat{\beta }}_{1}},\,\!</math> <math>{{\widehat{\eta }}_{1}}\,\!</math> are the parameters of the 393 psi data.


• <math>{{\widehat{\beta }}_{3}},</math>   <math>{{\widehat{\eta }}_{3}}</math> are the parameters of the 423 psi data.
*<math>{{\widehat{\beta }}_{2}},\,\!</math> <math>{{\widehat{\eta }}_{2}}\,\!</math> are the parameters of the 408 psi data.


[[Image:ALTAProbabilityplot.png|thumb|center|300px|]]
*<math>{{\widehat{\beta }}_{3}},\,\!</math> <math>{{\widehat{\eta }}_{3}}\,\!</math> are the parameters of the 423 psi data.


[[Image:ALTAProbabilityplot.png|center|600px|]]


Since the shape parameter, <math>\beta ,</math> is not common for the three stress levels, the average value is estimated.  
Since the shape parameter, <math>\beta ,\,\!</math> is not common for the three stress levels, the average value is estimated.  


::<math>{{\widehat{\beta }}_{common}}=4\,\!</math>


::<math>{{\widehat{\beta }}_{common}}=4</math>
Averaging the  betas  is one of many simple approaches available. One can also use a weighted average, since the uncertainty on beta is greater for smaller sample sizes. In most practical applications the value of <math>\widehat{\beta }\,\!</math> will vary (even though it is assumed constant) due to sampling error, etc. The variability in the value of <math>\widehat{\beta }\,\!</math> is a source of error when performing analysis by averaging the  betas. MLE analysis, which uses a common <math>\widehat{\beta }\,\!</math>, is not susceptible to this error. MLE analysis is the method of parameter estimation used in ALTA and it is explained in the next section.


 
Redraw each line with a <math>\widehat{\beta }=4\,\!</math>, and estimate the new  etas,  as follows:
Averaging the  <math>betas</math>  is one of many simple approaches available. One can also use a weighted average, since the uncertainty on beta is greater for smaller sample sizes. In most practical applications the value of  <math>\widehat{\beta }</math>  will vary (even though it is assumed constant) due to sampling error, etc. The variability in the value of  <math>\widehat{\beta }</math>  is a source of error when performing analysis by averaging the  <math>betas</math> . MLE analysis, which uses a common  <math>\widehat{\beta }</math> , is not susceptible to this error. MLE analysis is the method of parameter estimation used in ALTA and it is explained in the next section.
 
 
Redraw each line with a <math>\widehat{\beta }=4,</math>  and estimate the new  <math>etas,</math> as follows:


::<math>\begin{align}
::<math>\begin{align}
Line 83: Line 72:
  & {{\widehat{\eta }}_{2}}= & 5745 \\  
  & {{\widehat{\eta }}_{2}}= & 5745 \\  
  & {{\widehat{\eta }}_{3}}= & 4774   
  & {{\widehat{\eta }}_{3}}= & 4774   
\end{align}</math>
\end{align}\,\!</math>


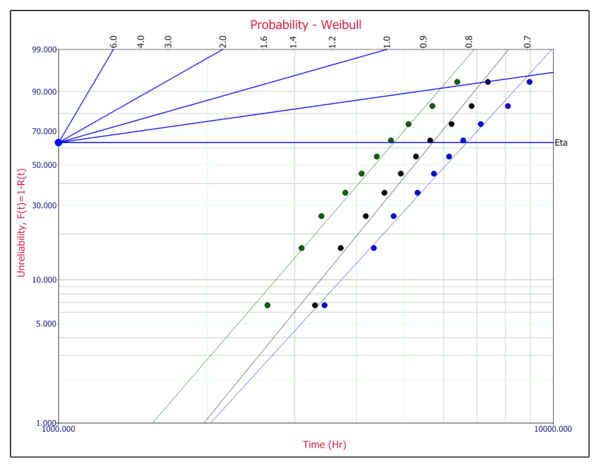
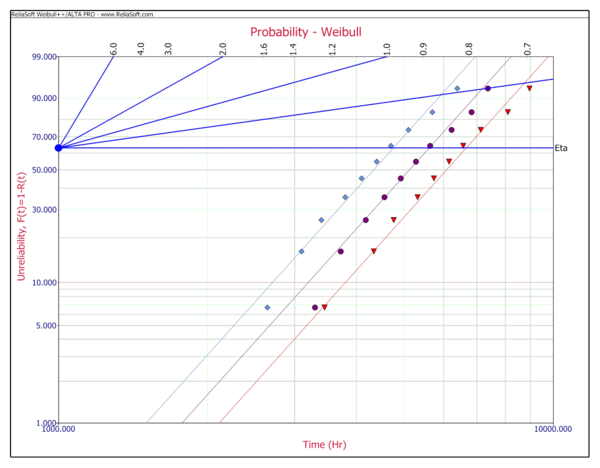
[[Image:ALTAProbabilityplot2.png|thumb|center|300px|]]
[[Image:ALTAProbabilityplot2.png|center|600px|]]


The IPL relationship is given by:  
The IPL relationship is given by:  


<br>
::<math>L(V)=\frac{1}{K{{V}^{n}}}\,\!</math>
::<math>L(V)=\frac{1}{K{{V}^{n}}}</math>


<br>
where <math>L\,\!</math> represents a quantifiable life measure (eta  in the Weibull case), <math>V\,\!</math> represents the stress level, <math>K\,\!</math> is one of the parameters, and <math>n\,\!</math> is another model parameter. The relationship is linearized by taking the logarithm of both sides which yields:  
where:
<br>
<math>L</math> represents a quantifiable life measure ( <math>\eta </math> in the Weibull case), <math>V</math> represents the stress level, <math>K</math> is one of the parameters, and <math>n</math> is another model parameter. The relationship is linearized by taking the logarithm of both sides which yields:  


<br>
::<math>\begin{align}
::<math>\ln (L)=-\ln K-n\ln V</math>
\ln (L)=-\ln K-n\ln V  
<br>
\end{align}\,\!</math>
where  <math>L=\eta </math> , (- <math>\ln K)</math>  is the intercept, and (- <math>n)</math> is the slope of the line.


<br>
where <math>L=\eta \,\!</math>, (<math>-\ln K)\,\!</math> is the intercept, and (<math>-n)\,\!</math> is the slope of the line.
The values of  <math>\eta </math> obtained previously are now plotted on a log-linear scale yielding the following plot:


The values of eta obtained previously are now plotted on a log-linear scale yielding the following plot:


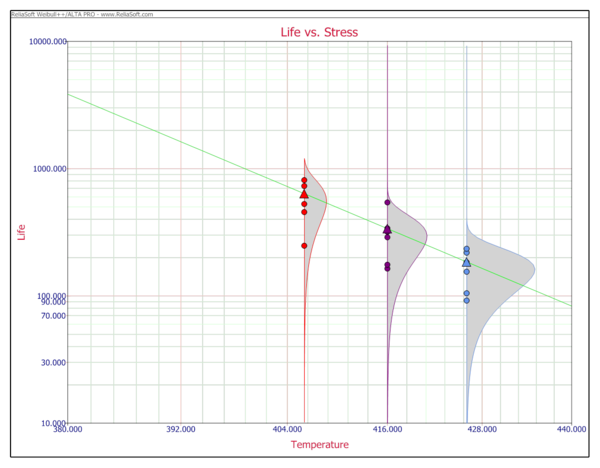
[[Image:ALTAlifevsstress.png|thumb|center|300px|]]
[[Image:ALTAlifevsstress.png|center|600px|]]


<br>
The slope of the line is the <math>n\,\!</math> parameter, which is obtained from the plot:
The slope of the line is the <math>n</math> parameter, which is obtained from the plot:


<br>
::<math>\begin{align}
::<math>\begin{align}
   & Slope=\ \frac{\ln ({{T}_{2}})-\ln ({{T}_{1}})}{\ln ({{V}_{2}})-\ln ({{V}_{1}})} =\ \frac{\ln (10,000)-\ln (6,000)}{\ln (360)-\ln (403)} =\ -4.5272   
   & Slope=\ \frac{\ln ({{T}_{2}})-\ln ({{T}_{1}})}{\ln ({{V}_{2}})-\ln ({{V}_{1}})} =\ \frac{\ln (10,000)-\ln (6,000)}{\ln (360)-\ln (403)} =\ -4.5272   
\end{align}</math>
\end{align}\,\!</math>
 


Thus:  
Thus:  


::<math>\widehat{n}=4.5272\,\!</math>


::<math>\widehat{n}=4.5272</math>
Solving the inverse power law equation with respect to <math>K\,\!</math> yields:


::<math>\widehat{K}=\frac{1}{L{{V}^{n}}}\,\!</math>


Solving the inverse power law equation with respect to  <math>K</math>  yields:
Substituting V=403, the corresponding L (from the plot), L=6,000 and the previously estimated <math>n\ \ :\,\!</math>  
 
 
::<math>\widehat{K}=\frac{1}{L{{V}^{n}}}</math>
 
 
Substituting V=403, the corresponding L (from the plot), L=6,000 and the previously estimated <math>n\ \ :</math>  
 


::<math>\begin{align}
::<math>\begin{align}
   & \widehat{K}=\ \frac{1}{6000\text{ }{{403}^{4.5272}}} =\ 2.67\cdot {{10}^{-16}}   
   & \widehat{K}=\ \frac{1}{6000\cdot{{403}^{4.5272}}} =\ 2.67\cdot {{10}^{-16}}   
\end{align}</math>
\end{align}\,\!</math>
 
<br>


==Comments on the Graphical Method==
==Comments on the Graphical Method==
<br>
Although the graphical method is simple, it is quite laborious. Furthermore, many issues surrounding its use require careful consideration. Some of these issues are presented next:
Although the graphical method is simple, it is quite laborious. Furthermore, many issues surrounding its use require careful consideration. Some of these issues are presented next:
<br>
• What happens when no failures are observed at one or more stress level? In this case, plotting methods cannot be employed. Discarding the data would be a mistake since every piece of life data information is important. 
 
• In the step at which the life-stress relationship is linearized and plotted to obtain its parameters, you must be able to linearize the function, which is not always possible.


• In real accelerated tests the data sets are small. Separating them and individually plotting them, and then subsequently replotting the results, increases the underlying error.
*What happens when no failures are observed at one or more stress level? In this case, plotting methods cannot be employed. Discarding the data would be a mistake since every piece of life data information is important.


• During initial parameter estimation, the parameter that is assumed constant will more than likely vary. What value do you use?
*In the step at which the life-stress relationship is linearized and plotted to obtain its parameters, you must be able to linearize the function, which is not always possible.


• Confidence intervals on all of the results cannot be ascertained using graphical methods.
*In real accelerated tests the data sets are small. Separating them and individually plotting them, and then subsequently replotting the results, increases the underlying error.
<br>
The maximum likelihood estimation parameter estimation method described next overcomes these shortfalls, and is the method utilized in ALTA.
<br>
<br>


=MLE (Maximum Likelihood) Parameter Estimation=
*During initial parameter estimation, the parameter that is assumed constant will more than likely vary. What value do you use?
<br>
The idea behind maximum likelihood parameter estimation is to determine the parameters that maximize the probability (likelihood) of the sample data. From a statistical point of view, the method of maximum likelihood is considered to be more robust (with some exceptions) and yields estimators with good statistical properties. In other words, MLE methods are versatile and apply to most models and to different types of data. In addition, they provide efficient methods for quantifying uncertainty through confidence bounds. Although the methodology for maximum likelihood estimation is simple, the implementation is mathematically intense. Using today's computer power, however, mathematical complexity is not a big obstacle. The MLE methodology is presented next.
<br>
==Background Theory==
<br>
This section presents the theory that underlies maximum likelihood estimation for complete data. <br>


*Confidence intervals on all of the results cannot be ascertained using graphical methods.


If  <math>x</math>  is a continuous random variable with  <math>pdf</math> :
The maximum likelihood estimation parameter estimation method described next overcomes these shortfalls, and is the method utilized in ALTA.
 


::<math>f(x;{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})</math>
=Maximum Likelihood Estimation (MLE) Method=
 
The idea behind maximum likelihood parameter estimation is to determine the parameters that maximize the probability (likelihood) of the sample data. From a statistical point of view, the method of maximum likelihood is considered to be more robust (with some exceptions) and yields estimators with good statistical properties. In other words, MLE methods are versatile and apply to most models and to different types of data. In addition, they provide efficient methods for quantifying uncertainty through confidence bounds. For a detailed discussion of this analysis method for a single life distribution, see [[Parameter_Estimation#Maximum_Likelihood_Parameter_Estimation|Maximum Likelihood Estimation]].
 
where  <math>{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}</math>  are  <math>k</math>  unknown constant parameters which need to be estimated, conduct an experiment and obtain  <math>N</math>  independent observations,  <math>{{x}_{1}},{{x}_{2}},</math>  ..., <math>{{x}_{N}}</math> . Then the likelihood function is given by the following product:
 
 
::<math>L({{x}_{1}},{{x}_{2}},...,{{x}_{N}}|{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})=L=\underset{i=1}{\overset{N}{\mathop \prod }}\,f({{x}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})</math>
 
 
::<math>i=1,2,...,N</math>
 
 
The logarithmic likelihood function is given by:
 
 
::<math>\Lambda =\ln L=\underset{i=1}{\overset{N}{\mathop \sum }}\,\ln f({{x}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})</math>
 
 
The maximum likelihood estimators (MLE) of  <math>{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}},</math>  are obtained by maximizing  <math>L</math>  or  <math>\Lambda .</math>
 
 
By maximizing  <math>\Lambda ,</math>  which is much easier to work with than  <math>L</math> , the maximum likelihood estimators (MLE) of <math>{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}</math>  are the simultaneous solutions of k equations such that:
 
 
::<math>\frac{\partial (\Lambda )}{\partial {{\theta }_{j}}}=0,j=1,2,...,k</math>
 
 
Even though it is common practice to plot the MLE solutions using median ranks (points are plotted according to median ranks and the line according to the MLE solutions), this is not completely accurate. As it can be seen from the equations above, the MLE method is independent of any kind of ranks or plotting methods. For this reason, many times the MLE solution appears not to track the data on the probability plot. This is perfectly acceptable since the two methods are independent of each other and in no way suggests that the solution is wrong.
<br>
<br>
===Illustrating the MLE Method Using the Exponential Distribution===
<br>
• To estimate  <math>\widehat{\lambda }</math>  for a sample of  <math>n</math>  units (all tested to failure), first obtain the likelihood function:


The maximum likelihood solution for accelerated life test data is formulated in the same way as described in [[Parameter_Estimation#Maximum_Likelihood_Parameter_Estimation|Maximum Likelihood Estimation]] for a single life distribution. However, in this case, the stress level of each individual observation is included in the likelihood function. Consider a continuous random variable <math>x(v),\,\!</math> where <math>v\,\!</math> is the stress. The  ''pdf''  of the random variable now becomes a function of both <math>x\,\!</math> and <math>v\,\!</math> :


::<math>\begin{align}
::<math>\begin{align}
  & L(\lambda |{{t}_{1}},{{t}_{2}},...,{{t}_{n}})=\ \underset{i=1}{\overset{n}{\mathop \prod }}\,f({{t}_{i}}) =\ \underset{i=1}{\overset{n}{\mathop \prod }}\,\lambda {{e}^{-\lambda {{t}_{i}}}} =\ {{\lambda }^{n}}\cdot {{e}^{-\lambda \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{t}_{i}}}} 
f(x,v;{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})
\end{align}</math>
\end{align}\,\!</math>
<br>
• Take the natural log of both sides:
 
 
::<math>\Lambda =\ln (L)=n\ln (\lambda )-\lambda \underset{i=1}{\overset{n}{\mathop \sum }}\,{{t}_{i}}</math>
<br>
• Obtain  <math>\tfrac{\partial \Lambda }{\partial \lambda }</math>  and set it equal to zero:
 
::<math>\frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-\underset{i=1}{\overset{n}{\mathop \sum }}\,{{t}_{i}}=0</math>
• Solve for  <math>\widehat{\lambda }</math>  or:
 
 
::<math>\hat{\lambda }=\frac{n}{\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{t}_{i}}}</math>
<br>
<br>
Notes on  <math>\lambda </math>
<br>
• Note that the value of  <math>\lambda </math>  is an estimate because if we obtain another sample from the same population and re-estimate  <math>\lambda </math> , the new value would differ from the one previously calculated.
 
• In plain language,  <math>\hat{\lambda }</math>  is an estimate of the true value of  <math>\lambda </math> .
 
• How close is the value of our estimate to the true value? To answer this question, one must first determine the distribution of the parameter, in this case  <math>\lambda </math> . This methodology introduces a new term, confidence interval, which allows us to specify a range for our estimate with a certain confidence level. The treatment of confidence intervals is integral to reliability engineering, and to all of statistics. (Confidence intervals are presented in [[Appendix A: Brief Statistical Background|Appendix A]].)
<br>
<br>
 
===Illustrating the MLE Method Using the Normal Distribution===
To obtain the MLE estimates for the mean,  <math>\bar{T},</math>  and standard deviation,  <math>{{\sigma }_{T}},</math>  for the normal distribution, start with the  <math>pdf</math>  of the normal distribution, which is given by:
 
<br>
::<math>f(T)=\frac{1}{{{\sigma }_{T}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{T-\bar{T}}{{{\sigma }_{T}}} \right)}^{2}}}}</math>


where <math>{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}\,\!</math> are <math>k\,\!</math> unknown constant parameters which need to be estimated. Conduct an experiment and obtain <math>N\,\!</math> independent observations, <math>{{x}_{1}},{{x}_{2}},...,{{x}_{N}}\,\!</math> each at a corresponding stress, <math>{{v}_{1}},\,\!</math> <math>{{v}_{2}},...,\,\!</math> <math>{{v}_{N}}\,\!</math>. Then the likelihood function for complete data is given by:


If  <math>{{T}_{1}},{{T}_{2}},...,{{T}_{N}}</math> are known times-to-failure (and with no suspensions), then the likelihood function is given by:
::<math>L(({{x}_{1}},\text{ }{{v}_{1}}),({{x}_{2}},\text{ }{{v}_{2}}),...,({{x}_{N}},\text{ }{{v}_{N}})|{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})=\underset{i=1}{\overset{N}{\mathop \prod }}\,f({{x}_{i}},{{v}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})\,\!</math>


::<math>L({{T}_{1}},{{T}_{2}},...,{{T}_{N}}|\bar{T},{{\sigma }_{T}})=L=\underset{i=1}{\overset{N}{\mathop \prod }}\,\left[ \frac{1}{{{\sigma }_{T}}\sqrt{2\pi }}{{e}^{-\tfrac{1}{2}{{\left( \tfrac{{{T}_{i}}-\bar{T}}{{{\sigma }_{T}}} \right)}^{2}}}} \right]</math>
<br>
::<math>L=\frac{1}{{{({{\sigma }_{T}}\sqrt{2\pi })}^{N}}}{{e}^{-\tfrac{1}{2}\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{\left( \tfrac{{{T}_{i}}-\bar{T}}{{{\sigma }_{T}}} \right)}^{2}}}}</math>
<br>
then:
<br>
::<math>\Lambda =\ln L=-\frac{N}{2}\ln (2\pi )-N\ln {{\sigma }_{T}}-\frac{1}{2}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( \frac{{{T}_{i}}-\bar{T}}{{{\sigma }_{T}}} \right)}^{2}}</math>
Then taking the partial derivatives of  <math>\Lambda </math>  with respect to each one of the parameters and setting it equal to zero yields:
::<math>\frac{\partial (\Lambda )}{\partial \bar{T}}=\frac{1}{\sigma _{T}^{2}}\underset{i=1}{\overset{N}{\mathop \sum }}\,({{T}_{i}}-\bar{T})=0</math>
and:
::<math>\frac{\partial (\Lambda )}{\partial {{\sigma }_{T}}}=-\frac{N}{{{\sigma }_{T}}}+\frac{1}{\sigma _{T}^{3}}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}}=0</math>
Solving the above equations simultaneously yields:
::<math>\bar{T}=\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{T}_{i}}</math>
and:
::<math>\begin{align}
  & \hat{\sigma }_{T}^{2}= & \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}} \\
&  &  \\
& {{{\hat{\sigma }}}_{T}}= & \sqrt{\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}}} 
\end{align}</math>
These solutions are only valid for data with no suspensions, i.e. all units are tested to failure. In cases in which suspensions are present, the methodology changes and the problem becomes much more complicated.
<br>
<br>
===Estimators===
As mentioned above, the parameters obtained from maximizing the likelihood function are estimators of the true value. It is clear that the sample size determines the accuracy of an estimator. If the sample size equals the whole population, then the estimator is the true value. Estimators have properties such as ''unbiasedness'', ''sufficiency'', ''consistency'', and ''efficiency''. Numerous books and papers deal with these properties and this coverage is beyond the scope of this reference.  However, we would like to briefly address unbiasedness and consistency.
<br>
<br>
===Unbiased Estimators===
An estimator is said to be unbiased if and only if the estimator  <math>\widehat{\theta }=d({{X}_{1,}}{{X}_{2,}}</math>  <math>...,{{X}_{n)}}</math>  satisfies the condition  <math>E\left[ \widehat{\theta } \right]</math>  <math>=\theta </math>  for all  <math>\theta \in \Omega .</math>  Note that  <math>E\left[ X \right]</math>  denotes the expected value of X and is defined by (for continuous distributions):
<br>
::<math>\begin{align}
  E\left[ X \right]=\ & \int_{\varpi }x\cdot f(x)dx \\
  X\in \ & \varpi 
\end{align}</math>
This implies that the true value is not consistently underestimated nor overestimated by an unbiased estimator.
<br>
<br>
===Consistent Estimators===
An unbiased estimator that converges more closely to the true value as the sample size increases is called a consistent estimator. In the example above, the standard deviation of the normal distribution was obtained using MLE. This estimator of the true standard deviation is a biased one. It can be shown [[Reference Appendix D: References|[4]]] that the consistent estimate of the variance and standard deviation for complete data (for the normal and lognormal distribution) is given by:
<br>
::<math>\begin{align}
::<math>\begin{align}
  & \hat{\sigma }_{T}^{2}= & \left[ \frac{N}{N-1} \right]\cdot \left[ \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}} \right]=\frac{1}{N-1}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}} \\
i=1,2,...,N  
& {{{\hat{\sigma }}}_{T}}= & \sqrt{\left[ \frac{N}{N-1} \right]\cdot \left[ \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}} \right]}=\sqrt{\frac{1}{N-1}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}}} 
\end{align}\,\!</math>
\end{align}</math>
 
<br>
Note that for larger values of N,  <math>\sqrt{\left[ N/(N-1) \right]}</math>  tends to 1.
 
<br>
 
=MLE of Accelerated Life Data=
<br>
Maximum likelihood offers a very powerful method in estimating the parameters of accelerated testing models, making possible the analysis of very complex models. In the beginning of this appendix, a graphical method for obtaining the parameters of accelerated testing models was illustrated. It involved estimating the parameters of the life distribution separately for each individual stress level, and then plotting the life-stress relationship in a linear manner on a separate life vs. stress plot. In other words, the life distribution and the life-stress relationship were treated separately. However, using the MLE method, the life distribution and the life-stress relationship can be treated as ONE complete model which describes both. This can be accomplished by including the life-stress relationship into the  <math>pdf</math>  of the life distribution.
<br>
<br>
==Background Theory==
<br>
The maximum likelihood for accelerated life testing analysis is formulated in the same way as shown previously. However, in this case the stress level of each individual observation is included in the likelihood function. Consider a continuous random variable  <math>x(v),</math>  where  <math>v</math>  is the stress. The  <math>pdf</math>  of the random variable now becomes a function of both  <math>x</math>  and  <math>v</math> :
 
<br>
::<math>f(x,v;{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})</math>
 
<br>
where  <math>{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}</math>  are  <math>k</math>  unknown constant parameters which need to be estimated. Conduct an experiment and obtain  <math>N</math>  independent observations,  <math>{{x}_{1}},{{x}_{2}},...,{{x}_{N}}</math>  each at a corresponding stress,  <math>{{v}_{1}},</math>  <math>{{v}_{2}},...,</math>  <math>{{v}_{N}}</math> . Then the likelihood function for complete data is given by:
 
::<math>L(({{x}_{1}},\text{ }{{v}_{1}}),({{x}_{2}},\text{ }{{v}_{2}}),...,({{x}_{N}},\text{ }{{v}_{N}})|{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})=\underset{i=1}{\overset{N}{\mathop \prod }}\,f({{x}_{i}},{{v}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})</math>
 
<br>
::<math>i=1,2,...,N</math>


<br>
The logarithmic likelihood function is given by:  
The logarithmic likelihood function is given by:  


<br>
::<math>\Lambda =\ln L=\underset{i=1}{\overset{N}{\mathop \sum }}\,\ln f({{x}_{i}},{{v}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})\,\!</math>
::<math>\Lambda =\ln L=\underset{i=1}{\overset{N}{\mathop \sum }}\,\ln f({{x}_{i}},{{v}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})</math>


The maximum likelihood estimators (MLE) of <math>{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}},\,\!</math> are obtained by maximizing <math>L\,\!</math> or <math>\Lambda .\,\!</math>


In this case, <math>{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}\,\!</math> are the parameters of the combined model which includes the parameters of the life distribution and the parameters of the life-stress relationship. Note that in the above equations, <math>N\,\!</math> is the total number of observations. This means that the sample size is no longer broken into the number of observations at each stress level. In the graphical method example, the sample size at the stress level of 20V was 4, and 15 at 36V. Using the above equations, however, the test's sample size is 19.


Once the parameters are estimated, they can be substituted back into the life distribution and the life-stress relationship.


The maximum likelihood estimators (MLE) of  <math>{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}},</math>  are obtained by maximizing  <math>L</math>  or  <math>\Lambda .</math>
==Example of MLE for Accelerated Life Data==
 
 
In this case,  <math>{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}</math>  are the parameters of the combined model which includes the parameters of the life distribution and the parameters of the life-stress relationship. Note that in the above equations,  <math>N</math>  is the total number of observations. This means that the sample size is no longer broken into the number of observations at each stress level. In Example 1, the sample size at the stress level of 20V was 4, and 15 at 36V. Using the above equations, however, the test's sample size is 19.
 
 
Once the parameters are estimated, they can be substituted back into the life distribution and the life-stress relationship.
<br>
<br>
===Example 2===
<br>
The following example illustrates the use of the MLE method on accelerated life test data. Consider the inverse power law relationship, given by:  
The following example illustrates the use of the MLE method on accelerated life test data. Consider the inverse power law relationship, given by:  


<br>
::<math>L(V)=\frac{1}{K{{V}^{n}}}\,\!</math>
::<math>L(V)=\frac{1}{K{{V}^{n}}}</math>


<br>
where <math>L\,\!</math> represents a quantifiable life measure, <math>V\,\!</math> represents the stress level, <math>K\,\!</math> is one of the parameters, and <math>n\,\!</math> is another model parameter.
where:
<br>
• <math>L</math> represents a quantifiable life measure, <math>V</math> represents the stress level, <math>K</math> is one of the parameters, and <math>n</math> is another model parameter.
Assume that the life at each stress follows a Weibull distribution, with a  <math>pdf</math>  given by:


<br>
Assume that the life at each stress follows a Weibull distribution, with a  ''pdf''  given by:  
::<math>f(t)=\frac{\beta }{\eta }{{\left( \frac{T}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}}</math>


<br>
::<math>f(t)=\frac{\beta }{\eta }{{\left( \frac{T}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}}\,\!</math>
where the time-to-failure, <math>t</math> , is a function of stress,  <math>V</math> .


<br>
where the time-to-failure, <math>t\,\!</math>, is a function of stress, <math>V\,\!</math>.
A common life measure needs to determined so that it can be easily included in the Weibull <math>pdf</math>. In this case, setting  <math>\eta =L(V)</math> (which is the life at 63.2%) and substituting in the Weibull <math>pdf</math>, yields the following IPL-Weibull  <math>pdf</math> :


<br>
A common life measure needs to determined so that it can be easily included in the Weibull ''pdf''. In this case, setting <math>\eta =L(V)\,\!</math> (which is the life at 63.2%) and substituting in the Weibull ''pdf'', yields the following IPL-Weibull  ''pdf'' :
::<math>f(t,V)=\beta K{{V}^{n}}{{\left( K{{V}^{n}}T \right)}^{\beta -1}}{{e}^{-{{\left( K{{V}^{n}}T \right)}^{\beta }}}}</math>


::<math>f(t,V)=\beta K{{V}^{n}}{{\left( K{{V}^{n}}T \right)}^{\beta -1}}{{e}^{-{{\left( K{{V}^{n}}T \right)}^{\beta }}}}\,\!</math>


The log-likelihood function for the complete data is given by:  
The log-likelihood function for the complete data is given by:  
<br>
Note that  <math>\beta </math>  is now the common shape parameter to solve for, along with  <math>K</math>  and  <math>n.</math> 


<br>
::<math>\Lambda =\ln L=\sum\limits_{i=1}^{N}{\ln \left( \beta K{{V}^{n}}{{\left( K{{V}^{n}}{{T}_{i}} \right)}^{\beta -1}}{{e}^{-{{\left( K{{V}^{n}}{{T}_{i}} \right)}^{\beta }}}} \right)}\,\!</math>


=Analysis of Censored Data=
Note that <math>\beta \,\!</math> is now the common shape parameter to solve for, along with <math>K\,\!</math> and <math>n.\,\!</math>
<br>
So far we have discussed parameter estimation methods for complete data only. We will expand on that approach in this section by including the maximum likelihood estimation method for right censored data. The method is based on the same principles covered previously but modified to take into account the fact that some of the data is censored. 
<br>
<br>
==MLE Analysis of Right Censored Data==
<br>
The maximum likelihood method is, at this point, by far the most appropriate analysis method for censored data. It is versatile and applicable to most accelerated life testing models. When performing maximum likelihood analysis, the likelihood function needs to be expanded to take into account the suspended items. A big advantage of using MLE when dealing with censored data is that each suspension term is included in the likelihood function. Thus, the estimates of the parameters are obtained from consideration of the entire population. Using MLE properties, confidence bounds can be obtained which also account for all the suspension terms. In the case of suspensions and where  <math>x</math>  is a continuous random variable with <math>pdf</math> and <math>cdf :</math>


::<math>\begin{align}
=Conclusions=
  &  & \ \ \ f(x;\,{{\theta }_{1}},\,{{\theta }_{2}},...,\,{{\theta }_{k}}) \\
&  & \ \ \ F(x;\,{{\theta }_{1}},\,{{\theta }_{2}},...,\,{{\theta }_{k}}) 
\end{align}</math>
 
 
where  <math>{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}</math>  are the  <math>k</math>  unknown parameters which need to be estimated from  <math>R</math>  observed failures at  <math>\left( {{T}_{1}},{{V}_{1}} \right),({{T}_{2}},{{V}_{2}})...({{T}_{R}},{{V}_{R}}),</math>  and  <math>M</math>  observed suspensions at  <math>\left( {{S}_{1}},V{{s}_{1}} \right),({{S}_{2}},V{{s}_{2}})...({{S}_{M}},V{{s}_{M}}),</math>  where  <math>{{V}_{R}}</math>  is the  <math>{{R}^{th}}</math>  stress level corresponding to the  <math>{{R}^{th}}</math>  observed failure, and  <math>V{{s}_{M}}</math>  is the  <math>{{M}^{th}}</math>  stress level corresponding to the  <math>{{M}^{th}}</math>  observed suspension. The likelihood function is then formulated as follows: 
 
 
::<math>\begin{align}
  &  L(\left( {{T}_{1}},{{V}_{1}} \right),({{T}_{2}},{{V}_{2}}) \\
&  ...,({{T}_{R}},{{V}_{R}}),\left( {{S}_{1}},V{{s}_{1}} \right),({{S}_{2}},V{{s}_{2}}) \\
&  ...,({{S}_{M}},V{{s}_{M}})|{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) \\
& = \underset{i=1}{\overset{R}{\mathop \prod }}\,f({{T}_{i}},{{V}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})\cdot \underset{j=1}{\overset{M}{\mathop \prod }}\,[1-F({{S}_{j}},V{{s}_{j}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})] 
\end{align}</math>
 
 
and the parameters are solved by maximizing this equation. In most cases, no closed form solution exists for this maximum, or for the parameters.
<br>
<br>
 
==Example 3==
<br>
Example 1 was repeated using MLE with the following results:
 
 
::<math>\begin{align}
  \widehat{\beta }=\ & 4.30218250 \\
\widehat{K}=\ & 1.61781534E-16 \\
\widehat{n}=\ & 4.61145743 
\end{align}</math>


In the individual analysis (probability plotting) the  <math>betas</math>  were averaged in order to estimate a common shape parameter. This introduced further uncertainties into the analysis. However, in this case (using MLE) the parameter  <math>\beta </math>  was estimated from the entire data set.
<br>
<br>
=Conclusions=
<br>
In this appendix, two methods for estimating the parameters of accelerated life testing models were presented. First, the graphical method was illustrated using a probability plotting method for obtaining the parameters of the life distribution. The parameters of the life-stress relationship were then estimated graphically by linearizing the model. However, not all life-stress relationships can be linearized. In addition, estimating the parameters of each individual distribution leads to an accumulation of uncertainties, depending on the number of failures and suspensions observed at each stress level. Furthermore, the slopes (shape parameters) of each individual distribution are rarely equal (common). Using the graphical method, one must estimate a common shape parameter (usually the average) and repeat the analysis. By doing so, further uncertainties are introduced on the estimates, and these are uncertainties that cannot be quantified. The second method, the Maximum Likelihood Estimation, treated both the life distribution and the life-stress relationship as one model, the parameters of that model can be estimated using the complete likelihood function. Doing so, a common shape parameter is estimated for the model, thus eliminating the uncertainties of averaging the individual shape parameters. All uncertainties are accounted for in the form of confidence bounds (presented in detail in [[Appendix_D:_Confidence_Bounds|Appendix D]]), which are quantifiable because they are obtained based on the overall model.
In this appendix, two methods for estimating the parameters of accelerated life testing models were presented. First, the graphical method was illustrated using a probability plotting method for obtaining the parameters of the life distribution. The parameters of the life-stress relationship were then estimated graphically by linearizing the model. However, not all life-stress relationships can be linearized. In addition, estimating the parameters of each individual distribution leads to an accumulation of uncertainties, depending on the number of failures and suspensions observed at each stress level. Furthermore, the slopes (shape parameters) of each individual distribution are rarely equal (common). Using the graphical method, one must estimate a common shape parameter (usually the average) and repeat the analysis. By doing so, further uncertainties are introduced on the estimates, and these are uncertainties that cannot be quantified. The second method, the Maximum Likelihood Estimation, treated both the life distribution and the life-stress relationship as one model, the parameters of that model can be estimated using the complete likelihood function. Doing so, a common shape parameter is estimated for the model, thus eliminating the uncertainties of averaging the individual shape parameters. All uncertainties are accounted for in the form of confidence bounds (presented in detail in [[Appendix_D:_Confidence_Bounds|Appendix D]]), which are quantifiable because they are obtained based on the overall model.
[[Category: Completed Theoretical Review]]

Latest revision as of 19:19, 15 September 2023

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images, more targeted search and the latest content available as a PDF. As of September 2023, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest reference at help.reliasoft.com/reference/accelerated_life_testing_data_analysis

Chapter Appendix B: Appendix B: Parameter Estimation


ALTAbox.png

Chapter Appendix B  
Appendix B: Parameter Estimation  

Synthesis-icon.png

Available Software:
ALTA

Examples icon.png

More Resources:
ALTA Examples


This appendix presents two methods for estimating the parameters of accelerated life test data analysis models (ALTA models). The graphical method, which is based on probability plotting or least squares (Rank Regression on X or Rank Regression on Y), has some limitations. Therefore, the Maximum Likelihood Estimation (MLE) method is used for all parameter estimation in ALTA.

Graphical Method

The graphical method for estimating the parameters of accelerated life data involves generating two types of plots. First, the life data at each individual stress level are plotted on a probability paper appropriate to the assumed life distribution (i.e., Weibull, exponential, or lognormal). This can be done using either Probability Plotting or Least Squares (Rank Regression).

The parameters of the distribution at each stress level are then estimated from the plot. Once these parameters have been estimated at each stress level, the second plot is created on a paper that linearizes the assumed life-stress relationship (e.g., Arrhenius, inverse power law, etc.). To do this, a life characteristic must be chosen to be plotted. The life characteristic can be any percentile, such as BX% life, the scale parameter, mean life, etc. The plotting paper used is a special type of paper that linearizes the life-stress relationship. For example, a log-log paper linearizes the inverse power law relationship, and a log-reciprocal paper linearizes the Arrhenius relationship. The parameters of the model are then estimated by solving for the slope and the intercept of the line.

ALTAB.1.png
ALTAB.1.1.png

Example of Graphical Method for Accelerated Life Data

Consider the following times-to-failure data at three different stress levels.

Stress 393 psi 408 psi 423 psi
Time Failed (hrs) 3450 3300 2645
4340 3720 3100
4760 4180 3400
5320 4560 3800
5740 4920 4100
6160 5280 4400
6580 5640 4700
7140 6233 5100
8101 6840 5700
8960 7380 6400

Estimate the parameters for a Weibull assumed life distribution and for the inverse power law life-stress relationship.

Solution

First the parameters of the Weibull distribution need to be determined. The data are individually analyzed (for each stress level) using the probability plotting method, or software such as ReliaSoft's Weibull++, with the following results:

[math]\displaystyle{ \begin{align} & [{{\widehat{\beta }}_{1}}= & 3.8,\text{ }{{\widehat{\eta }}_{1}}=6692] \\ & \text{ }\!\![\!\!\text{ }{{\widehat{\beta }}_{2}}= & 4.2,\text{ }{{\widehat{\eta }}_{2}}=5716] \\ & [{{\widehat{\beta }}_{3}}= & 4.0,\text{ }{{\widehat{\eta }}_{3}}=4774] \end{align}\,\! }[/math]

where:

  • [math]\displaystyle{ {{\widehat{\beta }}_{1}},\,\! }[/math] [math]\displaystyle{ {{\widehat{\eta }}_{1}}\,\! }[/math] are the parameters of the 393 psi data.
  • [math]\displaystyle{ {{\widehat{\beta }}_{2}},\,\! }[/math] [math]\displaystyle{ {{\widehat{\eta }}_{2}}\,\! }[/math] are the parameters of the 408 psi data.
  • [math]\displaystyle{ {{\widehat{\beta }}_{3}},\,\! }[/math] [math]\displaystyle{ {{\widehat{\eta }}_{3}}\,\! }[/math] are the parameters of the 423 psi data.
ALTAProbabilityplot.png

Since the shape parameter, [math]\displaystyle{ \beta ,\,\! }[/math] is not common for the three stress levels, the average value is estimated.

[math]\displaystyle{ {{\widehat{\beta }}_{common}}=4\,\! }[/math]

Averaging the betas is one of many simple approaches available. One can also use a weighted average, since the uncertainty on beta is greater for smaller sample sizes. In most practical applications the value of [math]\displaystyle{ \widehat{\beta }\,\! }[/math] will vary (even though it is assumed constant) due to sampling error, etc. The variability in the value of [math]\displaystyle{ \widehat{\beta }\,\! }[/math] is a source of error when performing analysis by averaging the betas. MLE analysis, which uses a common [math]\displaystyle{ \widehat{\beta }\,\! }[/math], is not susceptible to this error. MLE analysis is the method of parameter estimation used in ALTA and it is explained in the next section.

Redraw each line with a [math]\displaystyle{ \widehat{\beta }=4\,\! }[/math], and estimate the new etas, as follows:

[math]\displaystyle{ \begin{align} & {{\widehat{\eta }}_{1}}= & 6650 \\ & {{\widehat{\eta }}_{2}}= & 5745 \\ & {{\widehat{\eta }}_{3}}= & 4774 \end{align}\,\! }[/math]
ALTAProbabilityplot2.png

The IPL relationship is given by:

[math]\displaystyle{ L(V)=\frac{1}{K{{V}^{n}}}\,\! }[/math]

where [math]\displaystyle{ L\,\! }[/math] represents a quantifiable life measure (eta in the Weibull case), [math]\displaystyle{ V\,\! }[/math] represents the stress level, [math]\displaystyle{ K\,\! }[/math] is one of the parameters, and [math]\displaystyle{ n\,\! }[/math] is another model parameter. The relationship is linearized by taking the logarithm of both sides which yields:

[math]\displaystyle{ \begin{align} \ln (L)=-\ln K-n\ln V \end{align}\,\! }[/math]

where [math]\displaystyle{ L=\eta \,\! }[/math], ([math]\displaystyle{ -\ln K)\,\! }[/math] is the intercept, and ([math]\displaystyle{ -n)\,\! }[/math] is the slope of the line.

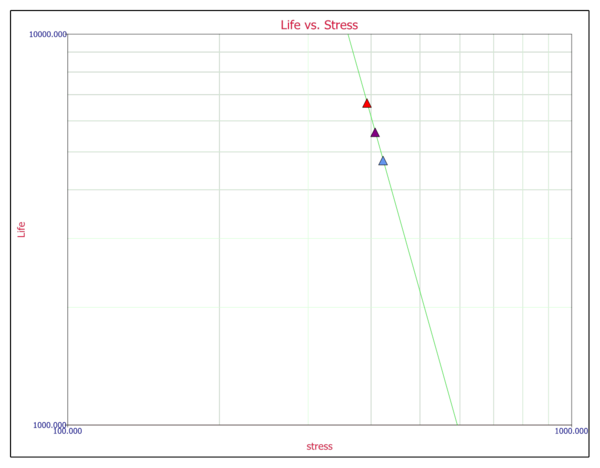
The values of eta obtained previously are now plotted on a log-linear scale yielding the following plot:

ALTAlifevsstress.png

The slope of the line is the [math]\displaystyle{ n\,\! }[/math] parameter, which is obtained from the plot:

[math]\displaystyle{ \begin{align} & Slope=\ \frac{\ln ({{T}_{2}})-\ln ({{T}_{1}})}{\ln ({{V}_{2}})-\ln ({{V}_{1}})} =\ \frac{\ln (10,000)-\ln (6,000)}{\ln (360)-\ln (403)} =\ -4.5272 \end{align}\,\! }[/math]

Thus:

[math]\displaystyle{ \widehat{n}=4.5272\,\! }[/math]

Solving the inverse power law equation with respect to [math]\displaystyle{ K\,\! }[/math] yields:

[math]\displaystyle{ \widehat{K}=\frac{1}{L{{V}^{n}}}\,\! }[/math]

Substituting V=403, the corresponding L (from the plot), L=6,000 and the previously estimated [math]\displaystyle{ n\ \ :\,\! }[/math]

[math]\displaystyle{ \begin{align} & \widehat{K}=\ \frac{1}{6000\cdot{{403}^{4.5272}}} =\ 2.67\cdot {{10}^{-16}} \end{align}\,\! }[/math]

Comments on the Graphical Method

Although the graphical method is simple, it is quite laborious. Furthermore, many issues surrounding its use require careful consideration. Some of these issues are presented next:

  • What happens when no failures are observed at one or more stress level? In this case, plotting methods cannot be employed. Discarding the data would be a mistake since every piece of life data information is important.
  • In the step at which the life-stress relationship is linearized and plotted to obtain its parameters, you must be able to linearize the function, which is not always possible.
  • In real accelerated tests the data sets are small. Separating them and individually plotting them, and then subsequently replotting the results, increases the underlying error.
  • During initial parameter estimation, the parameter that is assumed constant will more than likely vary. What value do you use?
  • Confidence intervals on all of the results cannot be ascertained using graphical methods.

The maximum likelihood estimation parameter estimation method described next overcomes these shortfalls, and is the method utilized in ALTA.

Maximum Likelihood Estimation (MLE) Method

The idea behind maximum likelihood parameter estimation is to determine the parameters that maximize the probability (likelihood) of the sample data. From a statistical point of view, the method of maximum likelihood is considered to be more robust (with some exceptions) and yields estimators with good statistical properties. In other words, MLE methods are versatile and apply to most models and to different types of data. In addition, they provide efficient methods for quantifying uncertainty through confidence bounds. For a detailed discussion of this analysis method for a single life distribution, see Maximum Likelihood Estimation.

The maximum likelihood solution for accelerated life test data is formulated in the same way as described in Maximum Likelihood Estimation for a single life distribution. However, in this case, the stress level of each individual observation is included in the likelihood function. Consider a continuous random variable [math]\displaystyle{ x(v),\,\! }[/math] where [math]\displaystyle{ v\,\! }[/math] is the stress. The pdf of the random variable now becomes a function of both [math]\displaystyle{ x\,\! }[/math] and [math]\displaystyle{ v\,\! }[/math] :

[math]\displaystyle{ \begin{align} f(x,v;{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) \end{align}\,\! }[/math]

where [math]\displaystyle{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}\,\! }[/math] are [math]\displaystyle{ k\,\! }[/math] unknown constant parameters which need to be estimated. Conduct an experiment and obtain [math]\displaystyle{ N\,\! }[/math] independent observations, [math]\displaystyle{ {{x}_{1}},{{x}_{2}},...,{{x}_{N}}\,\! }[/math] each at a corresponding stress, [math]\displaystyle{ {{v}_{1}},\,\! }[/math] [math]\displaystyle{ {{v}_{2}},...,\,\! }[/math] [math]\displaystyle{ {{v}_{N}}\,\! }[/math]. Then the likelihood function for complete data is given by:

[math]\displaystyle{ L(({{x}_{1}},\text{ }{{v}_{1}}),({{x}_{2}},\text{ }{{v}_{2}}),...,({{x}_{N}},\text{ }{{v}_{N}})|{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})=\underset{i=1}{\overset{N}{\mathop \prod }}\,f({{x}_{i}},{{v}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})\,\! }[/math]
[math]\displaystyle{ \begin{align} i=1,2,...,N \end{align}\,\! }[/math]

The logarithmic likelihood function is given by:

[math]\displaystyle{ \Lambda =\ln L=\underset{i=1}{\overset{N}{\mathop \sum }}\,\ln f({{x}_{i}},{{v}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})\,\! }[/math]

The maximum likelihood estimators (MLE) of [math]\displaystyle{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}},\,\! }[/math] are obtained by maximizing [math]\displaystyle{ L\,\! }[/math] or [math]\displaystyle{ \Lambda .\,\! }[/math]

In this case, [math]\displaystyle{ {{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}\,\! }[/math] are the parameters of the combined model which includes the parameters of the life distribution and the parameters of the life-stress relationship. Note that in the above equations, [math]\displaystyle{ N\,\! }[/math] is the total number of observations. This means that the sample size is no longer broken into the number of observations at each stress level. In the graphical method example, the sample size at the stress level of 20V was 4, and 15 at 36V. Using the above equations, however, the test's sample size is 19.

Once the parameters are estimated, they can be substituted back into the life distribution and the life-stress relationship.

Example of MLE for Accelerated Life Data

The following example illustrates the use of the MLE method on accelerated life test data. Consider the inverse power law relationship, given by:

[math]\displaystyle{ L(V)=\frac{1}{K{{V}^{n}}}\,\! }[/math]

where [math]\displaystyle{ L\,\! }[/math] represents a quantifiable life measure, [math]\displaystyle{ V\,\! }[/math] represents the stress level, [math]\displaystyle{ K\,\! }[/math] is one of the parameters, and [math]\displaystyle{ n\,\! }[/math] is another model parameter.

Assume that the life at each stress follows a Weibull distribution, with a pdf given by:

[math]\displaystyle{ f(t)=\frac{\beta }{\eta }{{\left( \frac{T}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{T}{\eta } \right)}^{\beta }}}}\,\! }[/math]

where the time-to-failure, [math]\displaystyle{ t\,\! }[/math], is a function of stress, [math]\displaystyle{ V\,\! }[/math].

A common life measure needs to determined so that it can be easily included in the Weibull pdf. In this case, setting [math]\displaystyle{ \eta =L(V)\,\! }[/math] (which is the life at 63.2%) and substituting in the Weibull pdf, yields the following IPL-Weibull pdf :

[math]\displaystyle{ f(t,V)=\beta K{{V}^{n}}{{\left( K{{V}^{n}}T \right)}^{\beta -1}}{{e}^{-{{\left( K{{V}^{n}}T \right)}^{\beta }}}}\,\! }[/math]

The log-likelihood function for the complete data is given by:

[math]\displaystyle{ \Lambda =\ln L=\sum\limits_{i=1}^{N}{\ln \left( \beta K{{V}^{n}}{{\left( K{{V}^{n}}{{T}_{i}} \right)}^{\beta -1}}{{e}^{-{{\left( K{{V}^{n}}{{T}_{i}} \right)}^{\beta }}}} \right)}\,\! }[/math]

Note that [math]\displaystyle{ \beta \,\! }[/math] is now the common shape parameter to solve for, along with [math]\displaystyle{ K\,\! }[/math] and [math]\displaystyle{ n.\,\! }[/math]

Conclusions

In this appendix, two methods for estimating the parameters of accelerated life testing models were presented. First, the graphical method was illustrated using a probability plotting method for obtaining the parameters of the life distribution. The parameters of the life-stress relationship were then estimated graphically by linearizing the model. However, not all life-stress relationships can be linearized. In addition, estimating the parameters of each individual distribution leads to an accumulation of uncertainties, depending on the number of failures and suspensions observed at each stress level. Furthermore, the slopes (shape parameters) of each individual distribution are rarely equal (common). Using the graphical method, one must estimate a common shape parameter (usually the average) and repeat the analysis. By doing so, further uncertainties are introduced on the estimates, and these are uncertainties that cannot be quantified. The second method, the Maximum Likelihood Estimation, treated both the life distribution and the life-stress relationship as one model, the parameters of that model can be estimated using the complete likelihood function. Doing so, a common shape parameter is estimated for the model, thus eliminating the uncertainties of averaging the individual shape parameters. All uncertainties are accounted for in the form of confidence bounds (presented in detail in Appendix D), which are quantifiable because they are obtained based on the overall model.

Retrieved from "https://www.reliawiki.com/index.php?title=Appendix_B:_Parameter_Estimation&oldid=65886"