|
|
| Line 9: |
Line 9: |
| {{alta data types}} | | {{alta data types}} |
|
| |
|
| ==Plots==
| | {{alta plot types}} |
| In addition to the probability plots required in life data analysis, accelerated life test data analysis utilizes a variety of stress-related plots. Each plot provides information crucial to performing accelerated life test analyses. The addition of stress dependency into the life equations introduces another dimension into the plots. This generates a whole new family of 3-dimensional (3D) plots. The following table summarizes the types of plots available in ReliaSoft's ALTA 7 and ALTA 7 PRO .
| |
| <br>
| |
| [[Image:ALTA3.8.gif|thumb|center|600px| ]]
| |
| <br>
| |
| Considerations relevant to the use of some of the plots available in ALTA are discussed in the sections that follow.
| |
| | |
| ===Probability Plots===
| |
| The probability plots used in accelerated life testing data analysis are similar to those used in life data analysis. The only difference is that each probability plot in accelerated testing is associated with the corresponding stress or stresses. Multiple lines will be plotted on a probability plot in ALTA, each corresponding to a different stress level. The information that can be obtained from probability plots includes: reliability with confidence bounds, warranty time with confidence bounds, shape and scale parameters, etc.
| |
| <br>
| |
| [[Image:pp4.1.gif|thumb|center|300px| A typical probability plot for three different stress levels.]]
| |
| <br>
| |
| | |
| ===Reliability and Unreliability Plots===
| |
| There are two types of reliability plots. The first type is a 2-dimensional plot of Reliability vs. Time for a given stress level. The second type is a 3-dimensional plot of the Reliability vs. Time vs. Stress. The 2-dimensional plot of reliability is just a section of the 3-dimensional plot at the desired stress level, as illustrated in Figure 2.
| |
| <br>
| |
| [[Image:gej6mg0e.gif|thumb|center|300px| Example of the relationship between 3D and 2D reliability plots.]]
| |
| <br>
| |
| A Reliability vs. Time plot provides reliability values at a given time and time at a given reliability. These can be plotted with or without confidence bounds. The same 2-dimensional and 3-dimensional plots are available for unreliability as well, and they are just the complement of the reliability plots.
| |
| <br>
| |
| ===Failure Rate Plots===
| |
| The instantaneous failure rate is a function of time and stress. For this reason, a 2-dimensional plot of Failure Rate vs. Time at a given stress and a 3-dimensional plot of Failure Rate vs. Time and Stress can be obtained in ALTA.
| |
| <br>
| |
| [[Image:ALTA3.6.gif|thumb|center|300px|3D failure rate plot. ]]
| |
| <br>
| |
| [[Image:2dfailrate.gif|thumb|center|300px|2D failure rate plot. ]]
| |
| <br>
| |
| A failure rate plot shows the expected number of failures per unit time at a particular stress level (e.g. failures per hour at 410K).
| |
| <br>
| |
| | |
| ===Pdf Plots===
| |
| The <math>pdf</math> is a function of time and stress. For this reason, a 2-dimensional plot of the <math>pdf</math> vs. Time at a given stress and a 3-dimensional plot of the <math>pdf</math> vs. Time and Stress can be obtained in ALTA.
| |
| <br>
| |
| [[Image:pdf2d.gif|thumb|center|300px| 2D ''pdf'' plot.]]
| |
| <br>
| |
| <br>
| |
| [[Image:pdf3d.gif|thumb|center|500px| 3D ''pdf'' plot.]]
| |
| | |
| A <math>pdf</math> plot represents the relative frequency of failures as a function of time and stress. Although the <math>pdf</math> plot is less important in most reliability applications than the other plots available in ALTA, it provides a good way of visualizing the distribution and its characteristics such as its shape, skewness, mode, etc.
| |
| | |
| ===Life-Stress Plots===
| |
| Life vs. Stress plots and Probability plots are the most important plot types in accelerated life testing analysis. Life vs. Stress plots are widely used for estimating the parameters of life-stress relationships. Any life measure can be plotted versus stress in the Life vs. Stress plots available in ALTA. Confidence bounds information on each life measure can also be plotted. The most widely used Life vs. Stress plots are the Arrhenius and the inverse power law plots. Fig. 7 illustrates a typical Arrhenius Life vs. Stress plot.
| |
| <br>
| |
| [[Image:ch4-7.gif|thumb|center|400px|Typical Arrhenius Life vs. Stress plot.]]
| |
| <br>
| |
|
| |
| Each line in Fig. 7 represents the path for extrapolating a life measure, such as a percentile, from one stress level to another. The slope and intercept of those lines are the parameters of the life-stress relationship (whenever the relationship can be linearized). The imposed pdfs represent the distribution of the data at each stress level.
| |
| | |
| ===Standard Deviation Plots===
| |
| Standard Deviation vs. Stress is a useful plot in accelerated life testing analysis and provides information about the spread of the data at each stress level.
| |
| <br>
| |
| [[Image:stdevplot.gif|thumb|center|400px|Standard Deviation vs. Stress plot.]]
| |
| <br>
| |
| <br>
| |
| | |
| ===Acceleration Factor Plots===
| |
| The acceleration factor is a unitless number that relates a product's life at an accelerated stress level to the life at the use stress level. It is defined by:
| |
| <br>
| |
| | |
| ::<math>{{A}_{F}}=\frac{{{L}_{u}}}{{{L}_{A}}}</math>
| |
| <br>
| |
| | |
| :where:
| |
| ::• <math>{{L}_{u}}</math> is the life at the use stress level.
| |
| ::• <math>{{L}_{A}}</math> is the life at the accelerated level.
| |
| <br>
| |
| As it can be seen in Eqn. (af), the acceleration factor depends on the life-stress relationship (i.e. Arrhenius, Eyring, etc.), and is thus a function of stress.
| |
| <br>
| |
| The Acceleration Factor vs. Stress plot is generated using Eqn. (af) at a constant use stress level and at a varying accelerated stress. In Figure 9, the Acceleration Factor vs. Stress was plotted for a constant use level of 300K. Since <math>{{L}_{A}}={{L}_{u}}</math> , the value of the acceleration factor at 300K is equal to 1. The acceleration factor for a temperature of 450K is approximately 8. This means that the life at the use level of 300K is eight times higher than the life at 450K.
| |
| <br>
| |
| [[Image:accfactplot.gif|thumb|center|400px|Acceleration Factor vs. Stress Plot.]]
| |
| <br>
| |
|
| |
|
| ==Residual Plots== | | ==Residual Plots== |
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images, more targeted search and the latest content available as a PDF. As of September 2023, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest reference at help.reliasoft.com/reference/accelerated_life_testing_data_analysis
|
Chapter 2: Accelerated Life Testing and ALTA
|
|

| Chapter 2
|
| Accelerated Life Testing and ALTA
|
Available Software:
ALTA
More Resources:
ALTA Examples
|
Accelerated Life Testing and ALTA
This chapter presents issues relevant to using the ALTA software package to analyze data collected in accelerated life tests. These issues include the types of data that can be analyzed and the types of plots that can be created to display analysis results.
For Deletion
Template:Alta plot types
Residual Plots
Residual analysis for reliability consists of analyzing the results of a regression analysis by assigning residual values to each data point in the data set. Plotting these residuals provides a very good tool in assessing model assumptions and revealing inadequacies in the model, as well as revealing extreme observations. Three types of residual plots are available in ALTA.
Standardized Residuals (SR)
The standardized residuals plot for the Weibull and lognormal distributions can be obtained in ALTA. Each plot type is discussed next.
SR for the Weibull Distribution
Once the parameters have been estimated, the standardized residuals for the Weibull distribution can be calculated by:
- [math]\displaystyle{ {{\widehat{e}}_{i}}=\widehat{\beta }\left[ \ln ({{T}_{i}})-\ln (\widehat{\eta }(V)) \right] }[/math]
Then, under the assumed model, these residuals should look like a sample from an extreme value distribution with a mean of 0. For the Weibull distribution the standardized residuals are plotted on a smallest extreme value probability paper. If the Weibull distribution adequately describes the data, then the standardized residuals should appear to follow a straight line on such a probability plot. Note that when an observation is censored (suspended), the corresponding residual is also censored.
SR for the Lognormal Distribution
Once the parameters have been estimated using rank regression, the fitted or calculated responses can be calculated by:
- [math]\displaystyle{ {{\widehat{e}}_{i}}=\frac{\ln ({{T}_{i}})-{{\widehat{\mu }}^{\prime }}}{{{\widehat{\sigma }}_{{{T}'}}}} }[/math]
Then, under the assumed model, the standardized residuals should be normally distributed with a mean of 0 and a standard deviation of 1 ( [math]\displaystyle{ \tilde{\ }N(0,1) }[/math] ). Consequently, the standardized residuals for the lognormal distribution are commonly displayed on a normal probability plot.
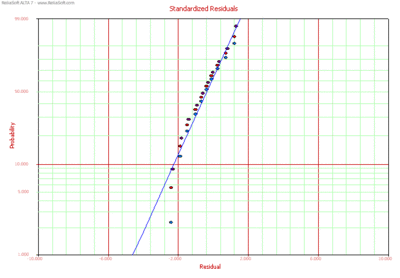
Probability plot of standardized residuals.
Cox-Snell Residuals
The Cox-Snell residuals are given by:
- [math]\displaystyle{ {{\widehat{e}}_{i}}=-\ln [R({{T}_{i}})] }[/math]
where [math]\displaystyle{ R({{T}_{i}}) }[/math] is the calculated reliability value at failure time [math]\displaystyle{ {{T}_{i}}. }[/math] The Cox-Snell residuals are plotted on an exponential probability paper.
- [math]\displaystyle{ }[/math]
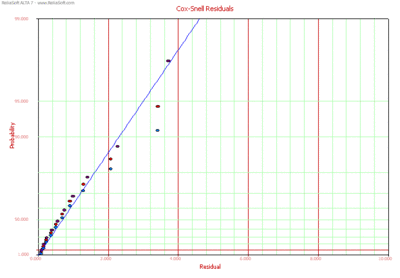
Probability plot of the Cox-Snell residuals.
Standardized vs Fitted Values
A Standardized vs. Fitted Value plot helps to detect behavior not modeled in the underlying relationship. However, when heavy censoring is present, the plot is more difficult to interpret. In a Standardized vs. Fitted Value plot, the standardized residuals are plotted versus the scale parameter of the underlying life distribution (which is a function of stress) on log-linear paper (linear on the Y-axis). Therefore, in the case of the Weibull distribution, the standardized residuals are plotted versus [math]\displaystyle{ \eta (V), }[/math] for the lognormal versus [math]\displaystyle{ {\mu }'(V), }[/math] and for the exponential versus [math]\displaystyle{ m(V). }[/math]
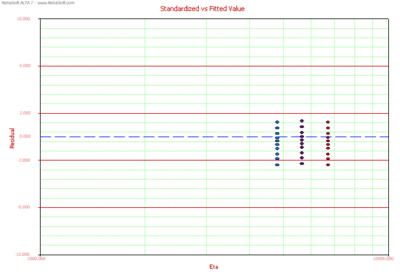
Standardized Residuals vs. Fitted Value.



