Crow-AMSAA Confidence Bounds Example

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.

---

This example appears in the Reliability Growth and Repairable System Analysis Reference book.

Using the values of $\hat{\beta }$ and $\hat{\lambda }$ estimated in the Failure Times - Example 1, calculate the 90% 2-sided confidence bounds on the cumulative and instantaneous failure intensity.

Solution

Fisher Matrix Bounds

The partial derivatives for the Fisher Matrix confidence bounds are:

$\begin{array}{rl}\frac{{\partial }^2\mathrm{\Lambda }}{\partial {\lambda }^2}=& -\frac{22}{{0.4239}^2}=-122.43\\ \frac{{\partial }^2\mathrm{\Lambda }}{\partial {\beta }^2}=& -\frac{22}{{0.6142}^2}-0.4239\cdot {620}^{0.6142}{(\ln 620)}^2=-967.68\\ \frac{{\partial }^2\mathrm{\Lambda }}{\partial \lambda \partial \beta }=& -{620}^{0.6142}\ln 620=-333.64\end{array}$

The Fisher Matrix then becomes:

$\begin{array}{rl}{\left[\begin{array}{cc}122.43& 333.64\\ 333.64& 967.68\end{array}\right]}^{-1}& =\left[\begin{array}{cc}Var(\hat{\lambda })& Cov(\hat{\beta },\hat{\lambda })\\ Cov(\hat{\beta },\hat{\lambda })& Var(\hat{\beta })\end{array}\right]\\ & =\left[\begin{array}{cc}0.13519969& -0.046614609\\ -0.046614609& 0.017105343\end{array}\right]\end{array}$

For $T=620$ hours, the partial derivatives of the cumulative and instantaneous failure intensities are:

$\begin{array}{rl}\frac{\partial {\lambda }_c(T)}{\partial \beta }=& \hat{\lambda }{T}^{\hat{\beta }-1}\ln (T)\\ =& 0.4239\cdot {620}^{-0.3858}\ln 620\\ =& 0.22811336\\ \frac{\partial {\lambda }_c(T)}{\partial \lambda }=& T^{\hat{\beta }-1}\\ =& {620}^{-0.3858}\\ =& 0.083694185\end{array}$

$\begin{array}{rl}\frac{\partial {\lambda }_i(T)}{\partial \beta }=& \hat{\lambda }{T}^{\hat{\beta }-1}+\hat{\lambda }\hat{\beta }{T}^{\hat{\beta }-1}\ln T\\ =& 0.4239\cdot {620}^{-0.3858}+0.4239\cdot 0.6142\cdot {620}^{-0.3858}\ln 620\\ =& 0.17558519\end{array}$

$\begin{array}{rl}\frac{\partial {\lambda }_i(T)}{\partial \lambda }=& \hat{\beta }{T}^{\hat{\beta }-1}\\ =& 0.6142\cdot {620}^{-0.3858}\\ =& 0.051404969\end{array}$

Therefore, the variances become:

$\begin{array}{rl}Var(\widehat{{\lambda }_c}(T))& ={0.22811336}^2\cdot 0.017105343+{0.083694185}^2\cdot 0.13519969-2\cdot 0.22811336\cdot 0.083694185\cdot 0.046614609\\ & =0.00005721408\\ Var(\widehat{{\lambda }_i}(T))& ={0.17558519}^2\cdot 0.01715343+{0.051404969}^2\cdot 0.13519969-2\cdot 0.17558519\cdot 0.051404969\cdot 0.046614609\\ & =0.0000431393\end{array}$

The cumulative and instantaneous failure intensities at $T=620$ hours are:

$\begin{array}{rl}{\lambda }_c(T)=& 0.03548\\ {\lambda }_i(T)=& 0.02179\end{array}$

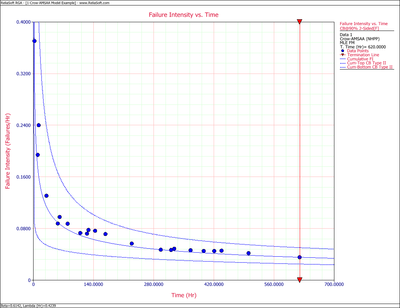
So, at the 90% confidence level and for $T=620$ hours, the Fisher Matrix confidence bounds for the cumulative failure intensity are:

$\begin{array}{rl}{[{\lambda }_c(T)]}_L=& 0.02499\\ {[{\lambda }_c(T)]}_U=& 0.05039\end{array}$

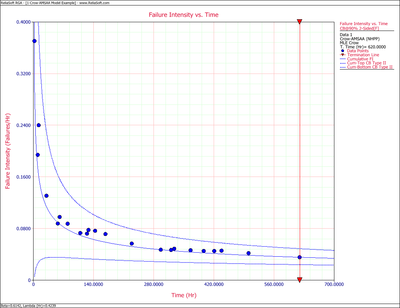
The confidence bounds for the instantaneous failure intensity are:

$\begin{array}{rl}{[{\lambda }_i(T)]}_L=& 0.01327\\ {[{\lambda }_i(T)]}_U=& 0.03579\end{array}$

The following figures display plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous failure intensity, respectively.

Crow Bounds

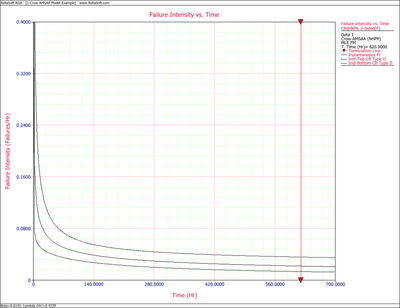
The Crow confidence bounds for the cumulative failure intensity at the 90% confidence level and for $T=620$ hours are:

$\begin{array}{rl}{[{\lambda }_c(T)]}_L=& \frac{{\chi }_{\frac{\alpha }{2},2N}^2}{2\cdot t}\\ =& \frac{29.787476}{2\ast 620}\\ =& 0.02402\\ {[{\lambda }_c(T)]}_U=& \frac{{\chi }_{1-\frac{\alpha }{2},2N+2}^2}{2\cdot t}\\ =& \frac{62.8296}{2\ast 620}\\ =& 0.05067\end{array}$

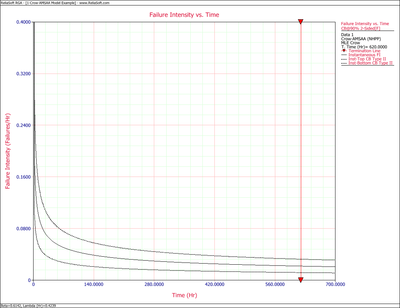
The Crow confidence bounds for the instantaneous failure intensity at the 90% confidence level and for $T=620$ hours are:

$\begin{array}{rl}{[{\lambda }_i(t)]}_L=& \frac{1}{{[MTB{F}_i]}_U}\\ =& \frac{1}{MTB{F}_i\cdot U}\\ =& 0.01179\end{array}$

$\begin{array}{rl}{[{\lambda }_i(t)]}_U=& \frac{1}{{[MTB{F}_i]}_L}\\ =& \frac{1}{MTB{F}_i\cdot L}\\ =& 0.03253\end{array}$

The following figures display plots of the Crow confidence bounds for the cumulative and instantaneous failure intensity, respectively.

Failure Times - Example 3

Calculate the confidence bounds on the cumulative and instantaneous MTBF for the data from the example given above.

Solution

Fisher Matrix Bounds

From the previous example:

$\begin{array}{rl}Var(\hat{\lambda })=& 0.13519969\\ Var(\hat{\beta })=& 0.017105343\\ Cov(\hat{\beta },\hat{\lambda })=& -0.046614609\end{array}$

And for $T=620$ hours, the partial derivatives of the cumulative and instantaneous MTBF are:

$\begin{array}{rl}\frac{\partial m_c(T)}{\partial \beta }=& -\frac{1}{\hat{\lambda }}{T}^{1-\hat{\beta }}\ln T\\ =& -\frac{1}{0.4239}{620}^{0.3858}\ln 620\\ =& -181.23135\\ \frac{\partial m_c(T)}{\partial \lambda }=& -\frac{1}{{\hat{\lambda }}^2}{T}^{1-\hat{\beta }}\\ =& -\frac{1}{{0.4239}^2}{620}^{0.3858}\\ =& -66.493299\\ \frac{\partial m_i(T)}{\partial \beta }=& -\frac{1}{\hat{\lambda }{\hat{\beta }}^2}{T}^{1-\beta }-\frac{1}{\hat{\lambda }\hat{\beta }}{T}^{1-\hat{\beta }}\ln T\\ =& -\frac{1}{0.4239\cdot {0.6142}^2}{620}^{0.3858}-\frac{1}{0.4239\cdot 0.6142}{620}^{0.3858}\ln 620\\ =& -369.78634\\ \frac{\partial m_i(T)}{\partial \lambda }=& -\frac{1}{{\hat{\lambda }}^2\hat{\beta }}{T}^{1-\hat{\beta }}\\ =& -\frac{1}{{0.4239}^2\cdot 0.6142}\cdot {620}^{0.3858}\\ =& -108.26001\end{array}$

Therefore, the variances become:

$\begin{array}{rl}Var({\hat{m}}_c(T))=& {(-181.23135)}^2\cdot 0.017105343+{(-66.493299)}^2\cdot 0.13519969\\ & -2\cdot (-181.23135)\cdot (-66.493299)\cdot 0.046614609\\ =& 36.113376\end{array}$

$\begin{array}{rl}Var({\hat{m}}_i(T))=& {(-369.78634)}^2\cdot 0.017105343+{(-108.26001)}^2\cdot 0.13519969\\ & -2\cdot (-369.78634)\cdot (-108.26001)\cdot 0.046614609\\ =& 191.33709\end{array}$

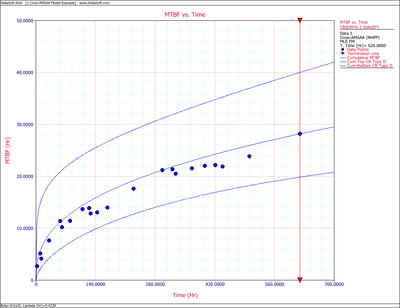
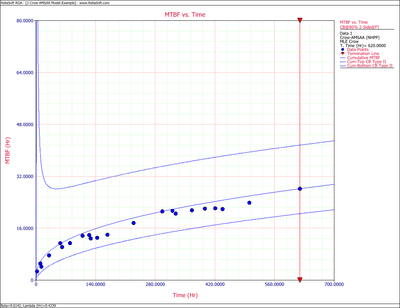
So, at 90% confidence level and $T=620$ hours, the Fisher Matrix confidence bounds are:

$\begin{array}{rl}{[m_c(T)]}_L=& {\hat{m}}_c(t)e^{-z_{\alpha }\sqrt{Var({\hat{m}}_c(t))}/{\hat{m}}_c(t)}\\ =& 19.84581\\ {[m_c(T)]}_U=& {\hat{m}}_c(t)e^{z_{\alpha }\sqrt{Var({\hat{m}}_c(t))}/{\hat{m}}_c(t)}\\ =& 40.01927\end{array}$

$\begin{array}{rl}{[m_i(T)]}_L=& {\hat{m}}_i(t)e^{-z_{\alpha }\sqrt{Var({\hat{m}}_i(t))}/{\hat{m}}_i(t)}\\ =& 27.94261\\ {[m_i(T)]}_U=& {\hat{m}}_i(t)e^{z_{\alpha }\sqrt{Var({\hat{m}}_i(t))}/{\hat{m}}_i(t)}\\ =& 75.34193\end{array}$

The following two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBFs.

Crow Bounds

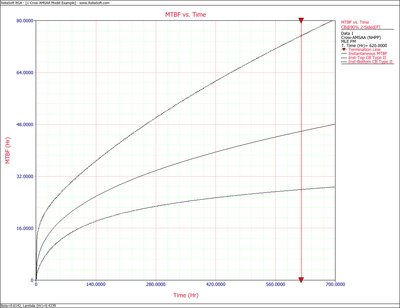
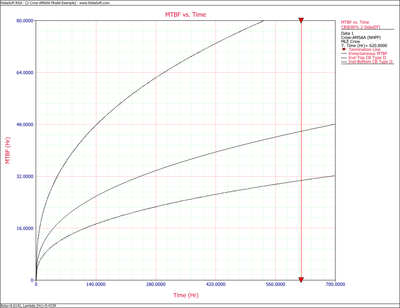
The Crow confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% confidence level and for $T=620$ hours are:

$\begin{array}{rl}{[m_c(T)]}_L=& \frac{1}{{[{\lambda }_c(T)]}_U}\\ =& 20.5023\\ {[m_c(T)]}_U=& \frac{1}{{[{\lambda }_c(T)]}_L}\\ =& 41.6282\end{array}$

$\begin{array}{rl}{[MTB{F}_i]}_L=& MTB{F}_i\cdot {\mathrm{\Pi }}_1\\ =& 30.7445\\ {[MTB{F}_i]}_U=& MTB{F}_i\cdot {\mathrm{\Pi }}_2\\ =& 84.7972\end{array}$

The figures below show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.

Confidence bounds can also be obtained on the parameters $\hat{\beta }$ and $\hat{\lambda }$. For Fisher Matrix confidence bounds:

$\begin{array}{rl}{\beta }_L=& \hat{\beta }{e}^{z_{\alpha }\sqrt{Var(\hat{\beta })}/\hat{\beta }}\\ =& 0.4325\\ {\beta }_U=& \hat{\beta }{e}^{-z_{\alpha }\sqrt{Var(\hat{\beta })}/\hat{\beta }}\\ =& 0.8722\end{array}$

and:

$\begin{array}{rl}{\lambda }_L=& \hat{\lambda }{e}^{z_{\alpha }\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}\\ =& 0.1016\\ {\lambda }_U=& \hat{\lambda }{e}^{-z_{\alpha }\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}\\ =& 1.7691\end{array}$

For Crow confidence bounds:

$\begin{array}{rl}{\beta }_L=& 0.4527\\ {\beta }_U=& 0.9350\end{array}$

and:

$\begin{array}{rl}{\lambda }_L=& 0.2870\\ {\lambda }_U=& 0.5827\end{array}$