Template:Estimating equation using the cw

Estimating [math]\displaystyle{ P\left[ {{t}_{2}}\ge {{t}_{1}} \right] }[/math] Using the Comparison Wizard

Another methodology, suggested by Gerald G. Brown and Herbert C. Rutemiller, is to estimate the probability of whether the times-to-failure of one population are better or worse than the times-to-failure of the second. The equation used to estimate this probability is given by:

[math]\displaystyle{ P\left[ {{t}_{2}}\ge {{t}_{1}} \right]=\mathop{}_{0}^{\infty }{{f}_{1}}(t)\cdot {{R}_{2}}(t)\cdot dt }[/math]

where [math]\displaystyle{ {{f}_{1}}(t) }[/math] is the [math]\displaystyle{ pdf }[/math] of the first distribution and [math]\displaystyle{ {{R}_{2}}(t) }[/math] is the reliability function of the second distribution. The evaluation of the superior data set is based on whether this probability is smaller or greater than 0.5. If the probability is equal to 0.5, that is equivalent to saying the two distributions are identical.

If given two alternate designs with life test data, where X and Y represent the life test data from two different populations, and if we simply wanted to choose the component at time [math]\displaystyle{ t }[/math] with the higher reliability, one choice would be to select the component with the higher reliability at time [math]\displaystyle{ t }[/math] . However, if we wanted to design a product as long-lived as possible, we would want to calculate the probability that the entire distribution of one product is better than the other and choose X or Y when this probability is above or below 0.50 respectively.

The statement that the probability that X is greater or equal to Y can be interpreted as follows:

• If [math]\displaystyle{ P=0.50 }[/math] , then the statement is equivalent to saying that both X and Y are equal.

• If [math]\displaystyle{ P\lt 0.50 }[/math] or, for example, [math]\displaystyle{ P=0.10 }[/math] , then the statement is equivalent to saying that [math]\displaystyle{ P=1-0.10=0.90 }[/math] , or Y is better than X with a 90% probability.

Weibull++'s Comparison Wizard allows you to perform such calculations. The disadvantage of this method is that the sample sizes are not taken into account, thus one should avoid using this method of comparison when the sample sizes are different.

Example 16

Using the data presented in Example 15, use Weibull++'s Comparison Wizard to estimate the probability that units from the new design will outlast units from the old design.

Solution to Example 16

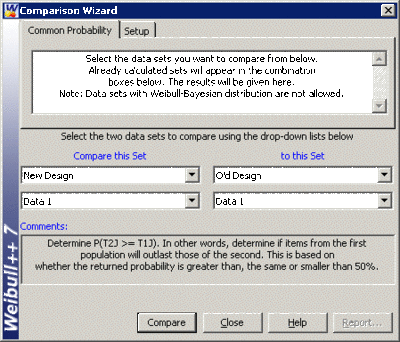
After entering the Example 15's data sets into two different folios (or data sheets within the same folio) and analyzing them (in this case, the two data sets were analyzed using the two-parameter distribution and MLE), select Tests of Comparison from the Tools menu to accessthe Comparison Wizard. Specify the data sets that are being compared:

[math]\displaystyle{ }[/math]

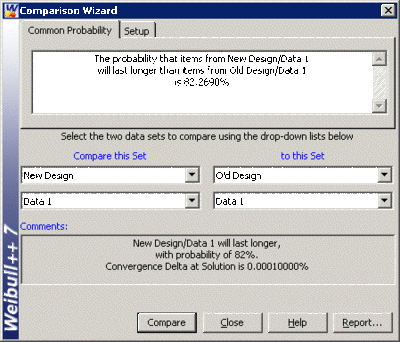
Click Compare. The result of the comparison is displayed in the next window.

[math]\displaystyle{ }[/math]