Recurrent Events Data Non-parameteric MCF Example

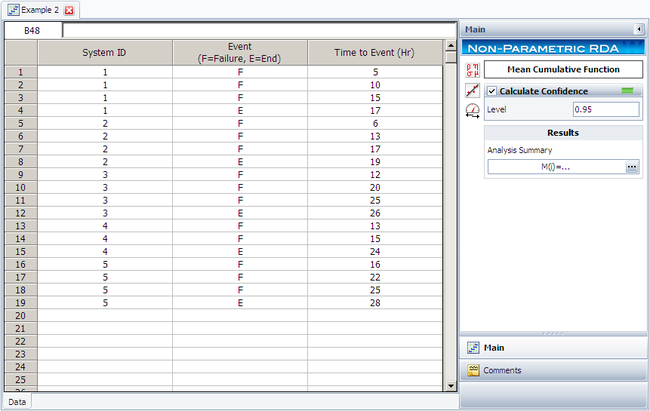
A health care company maintains five identical pieces of equipment used by a hospital. When a piece of equipment fails, the company sends a crew to repair it. The following table gives the failure and censoring ages for each machine, where the + sign indicates a censoring age.

$\begin{array}{cc}EquipmentID& Months\\ \text{1}& \text{5, 10 , 15, 17+}\\ \text{2}& \text{6, 13, 17, 19+}\\ \text{3}& \text{12, 20, 25, 26+}\\ \text{4}& \text{13, 15, 24+}\\ \text{5}& \text{16, 22, 25, 28+}\end{array}$

Estimate the MCF values, with 95% confidence bounds.

Solution

The MCF estimates are obtained as follows:

$\begin{array}{cccccc}ID& Months(t_i)& State& r_i& 1/r_i& M^{\ast }(t_i)\\ \text{1}& \text{5}& \text{F}& \text{5}& \text{0}\text{.20}& \text{0}\text{.20}\\ \text{2}& \text{6}& \text{F}& \text{5}& \text{0}\text{.20}& \text{0}\text{.20 + 0}\text{.20 = 0}\text{.40}\\ \text{1}& \text{10}& \text{F}& \text{5}& \text{0}\text{.20}& \text{0}\text{.40 + 0}\text{.20 = 0}\text{.60}\\ \text{3}& \text{12}& \text{F}& \text{5}& \text{0}\text{.20}& \text{0}\text{.60 + 0}\text{.20 = 0}\text{.80}\\ \text{2}& \text{13}& \text{F}& \text{5}& \text{0}\text{.20}& \text{0}\text{.80 + 0}\text{.20 = 1}\text{.00}\\ \text{4}& \text{13}& \text{F}& \text{5}& \text{0}\text{.20}& \text{1}\text{.00 + 0}\text{.20 = 1}\text{.20}\\ \text{1}& \text{15}& \text{F}& \text{5}& \text{0}\text{.20}& \text{1}\text{.20 + 0}\text{.20 = 1}\text{.40}\\ \text{4}& \text{15}& \text{F}& \text{5}& \text{0}\text{.20}& \text{1}\text{.40 + 0}\text{.20 = 1}\text{.60}\\ \text{5}& \text{16}& \text{F}& \text{5}& \text{0}\text{.20}& \text{1}\text{.60 + 0}\text{.20 = 1}\text{.80}\\ \text{2}& \text{17}& \text{F}& \text{5}& \text{0}\text{.20}& \text{1}\text{.80 + 0}\text{.20 = 2}\text{.00}\\ \text{1}& \text{17}& \text{S}& \text{4}& & \\ \text{2}& \text{19}& \text{S}& \text{3}& & \\ \text{3}& \text{20}& \text{F}& \text{3}& \text{0}\text{.33}& \text{2}\text{.00 + 0}\text{.33 = 2}\text{.33}\\ \text{5}& \text{22}& \text{F}& \text{3}& \text{0}\text{.33}& \text{2}\text{.33 + 0}\text{.33 = 2}\text{.66}\\ \text{4}& \text{24}& \text{S}& \text{2}& & \\ \text{3}& \text{25}& \text{F}& \text{2}& \text{0}\text{.50}& \text{2}\text{.66 + 0}\text{.50 = 3}\text{.16}\\ \text{5}& \text{25}& \text{F}& \text{2}& \text{0}\text{.50}& \text{3}\text{.16 + 0}\text{.50 = 3}\text{.66}\\ \text{3}& \text{26}& \text{S}& \text{1}& & \\ \text{5}& \text{28}& \text{S}& \text{0}& & \end{array}$

Using the MCF variance equation, the following table of variance values can be obtained:

ID	Months	State	$r_i$	$Va{r}_i$
1	5	F	5	$(\frac{1}{5}{)}^2[(1-\frac{1}{5}{)}^2+4(0-\frac{1}{5}{)}^2]=0.032$
2	6	F	5	$0.032+(\frac{1}{5}{)}^2[(1-\frac{1}{5}{)}^2+4(0-\frac{1}{5}{)}^2]=0.064$
1	10	F	5	$0.064+(\frac{1}{5}{)}^2[(1-\frac{1}{5}{)}^2+4(0-\frac{1}{5}{)}^2]=0.096$
3	12	F	5	$0.096+(\frac{1}{5}{)}^2[(1-\frac{1}{5}{)}^2+4(0-\frac{1}{5}{)}^2]=0.128$
2	13	F	5	$0.128+(\frac{1}{5}{)}^2[(1-\frac{1}{5}{)}^2+4(0-\frac{1}{5}{)}^2]=0.160$
4	13	F	5	$0.160+(\frac{1}{5}{)}^2[(1-\frac{1}{5}{)}^2+4(0-\frac{1}{5}{)}^2]=0.192$
1	15	F	5	$0.192+(\frac{1}{5}{)}^2[(1-\frac{1}{5}{)}^2+4(0-\frac{1}{5}{)}^2]=0.224$
4	15	F	5	$0.224+(\frac{1}{5}{)}^2[(1-\frac{1}{5}{)}^2+4(0-\frac{1}{5}{)}^2]=0.256$
5	16	F	5	$0.256+(\frac{1}{5}{)}^2[(1-\frac{1}{5}{)}^2+4(0-\frac{1}{5}{)}^2]=0.288$
2	17	F	5	$0.288+(\frac{1}{5}{)}^2[(1-\frac{1}{5}{)}^2+4(0-\frac{1}{5}{)}^2]=0.320$
1	17	S	4
2	19	S	3
3	20	F	3	$0.320+(\frac{1}{3}{)}^2[(1-\frac{1}{3}{)}^2+2(0-\frac{1}{3}{)}^2]=0.394$
5	22	F	3	$0.394+(\frac{1}{3}{)}^2[(1-\frac{1}{3}{)}^2+2(0-\frac{1}{3}{)}^2]=0.468$
4	24	S	2
3	25	F	2	$0.468+(\frac{1}{2}{)}^2[(1-\frac{1}{2}{)}^2+(0-\frac{1}{2}{)}^2]=0.593$
5	25	F	2	$0.593+(\frac{1}{2}{)}^2[(1-\frac{1}{2}{)}^2+(0-\frac{1}{2}{)}^2]=0.718$
3	26	S	1
5	28	S	0

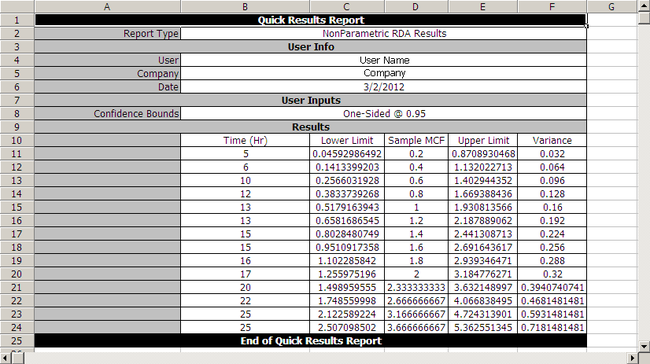
Using the equation for the MCF bounds and $K_5=1.644$ for a 95% confidence level, the confidence bounds can be obtained as follows:

$\begin{array}{ccccccc}ID& Months& State& MC{F}_i& Va{r}_i& MC{F}_{L_i}& MC{F}_{U_i}\\ \text{1}& \text{5}& \text{F}& \text{0}\text{.20}& \text{0}\text{.032}& 0.0459& 0.8709\\ \text{2}& \text{6}& \text{F}& \text{0}\text{.40}& \text{0}\text{.064}& 0.1413& 1.1320\\ \text{1}& \text{10}& \text{F}& \text{0}\text{.60}& \text{0}\text{.096}& 0.2566& 1.4029\\ \text{3}& \text{12}& \text{F}& \text{0}\text{.80}& \text{0}\text{.128}& 0.3834& 1.6694\\ \text{2}& \text{13}& \text{F}& \text{1}\text{.00}& \text{0}\text{.160}& 0.5179& 1.9308\\ \text{4}& \text{13}& \text{F}& \text{1}\text{.20}& \text{0}\text{.192}& 0.6582& 2.1879\\ \text{1}& \text{15}& \text{F}& \text{1}\text{.40}& \text{0}\text{.224}& 0.8028& 2.4413\\ \text{4}& \text{15}& \text{F}& \text{1}\text{.60}& \text{0}\text{.256}& 0.9511& 2.6916\\ \text{5}& \text{16}& \text{F}& \text{1}\text{.80}& \text{0}\text{.288}& 1.1023& 2.9393\\ \text{2}& \text{17}& \text{F}& \text{2}\text{.00}& \text{0}\text{.320}& 1.2560& 3.1848\\ \text{1}& \text{17}& \text{S}& & & & \\ \text{2}& \text{19}& \text{S}& & & & \\ \text{3}& \text{20}& \text{F}& \text{2}\text{.33}& \text{0}\text{.394}& 1.4990& 3.6321\\ \text{5}& \text{22}& \text{F}& \text{2}\text{.66}& \text{0}\text{.468}& 1.7486& 4.0668\\ \text{4}& \text{24}& \text{S}& & & & \\ \text{3}& \text{25}& \text{F}& \text{3}\text{.16}& \text{0}\text{.593}& 2.1226& 4.7243\\ \text{5}& \text{25}& \text{F}& \text{3}\text{.66}& \text{0}\text{.718}& 2.5071& 5.3626\\ \text{3}& \text{26}& \text{S}& & & & \\ \text{5}& \text{28}& \text{S}& & & & \end{array}$

The analysis presented in this example can be performed automatically in Weibull++'s non-parametric RDA folio, as shown next.

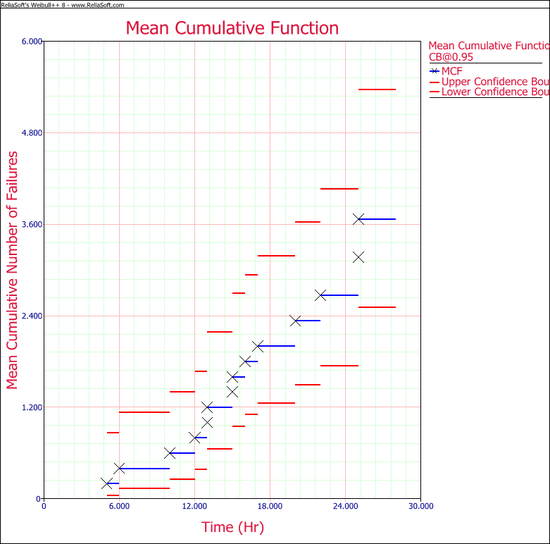
Note: In the folio above, the $F$ refers to failures and $E$ refers to suspensions (or censoring ages). The results, with calculated MCF values and upper and lower 95% confidence limits, are shown next along with the graphical plot.