Non-Parametric Binomial Test Design Example
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example appears in the Life Data Analysis Reference book.
Example: Non-Parametric Binomial Test Design
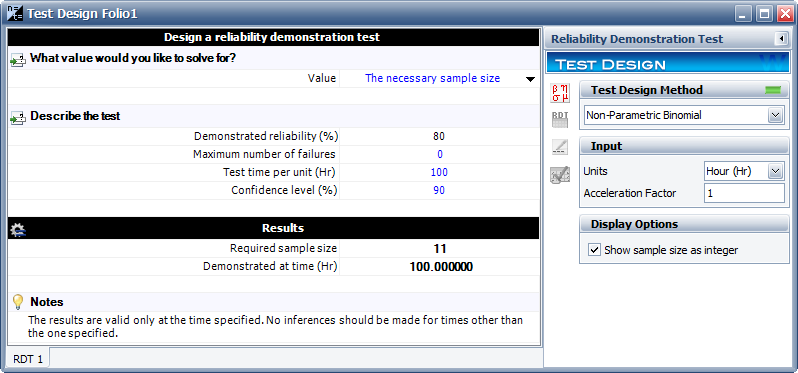
A reliability engineer wants to design a zero-failure demonstration test in order to demonstrate a reliability of 80% at a 90% confidence level. What is the required sample size?
Solution
By substituting [math]\displaystyle{ f=0 }[/math] (since it a zero-failure test) the non-parametric binomial equation becomes:
- [math]\displaystyle{ \begin{align} 1-CL=R^{n} \end{align} }[/math]
So now the required sample size can be easily solved for any required reliability and confidence level. The result of this test design was obtained using Weibull++ and is:
The result shows that 11 samples are needed. Note that the time value shown in the above figure is chance indicative and not part of the test design (the "Test time per unit" that was input will be the same as the "Demonstrated at time" value for the results). If those 11 samples are run for the required demonstration time and no failures are observed, then a reliability of 80% with a 90% confidence level has been demonstrated. If the reliability of the system is less than or equal to 80%, the chance of passing this test is 1-CL = 0.1, which is the Type II error. Therefore, the non-parametric binomial equation determines the sample size by controlling for the Type II error.
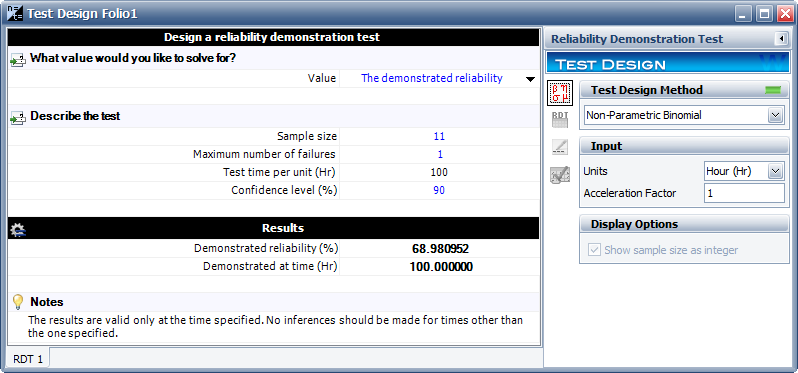
If 11 samples are used and one failure is observed by the end of the test, then the demonstrated reliability will be less than required. The demonstrated reliability is 68.98% as shown below.