Template:Weibull Parametric Recurrent Events Data Analysis

Parametric Recurrent Event Data Analysis

Weibull++'s parametric RDA folio is a tool for modeling recurrent event data. It can capture the trend, estimate the rate and predict the total number of recurrences. The failure and repair data of a repairable system can be treated as one type of recurrence data. Past and current repairs may affect the future failure process. For most recurrent events, time (distance, cycles, etc.) is a key factor. With time, the recurrence rate may remain constant, increase or decrease. For other recurrent events, not only the time, but also the number of events can affect the recurrence process (e.g., the debugging process in software development). The parametric analysis approach utilizes the General Renewal Process (GRP) model [28]. In this model, the repair time is assumed to be negligible so that the processes can be viewed as point processes. This model provides a way to describe the rate of occurrence of events over time, such as in the case of data obtained from a repairable system. This model is particularly useful in modeling the failure behavior of a specific system and understanding the effects of the repairs on the age of that system. For example, consider a system that is repaired after a failure, where the repair does not bring the system to an as-good-as-new or an as-bad-as-old condition. In other words, the system is partially rejuvenated after the repair. Traditionally, in as-bad-as-old repairs, also known as minimal repairs, the failure data from such a system would have been modeled using a homogeneous or non-homogeneous Poisson process (NHPP). On rare occasions, a Weibull distribution has been used as well in cases where the system is almost as-good-as-new after the repair, also known as a perfect renewal process (PRP). However, for the intermediate states after the repair, there has not been a commercially available model, even though many models have been proposed in literature. In Weibull++, the GRP model provides the capability to model systems with partial renewal (general repair or imperfect repair/maintenance) and allows for a variety of predictions such as reliability, expected failures, etc.

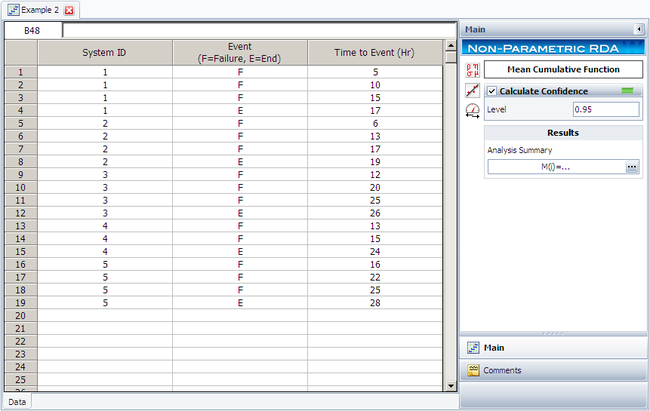
Recurrent Event Data Analysis (RDA) is used in various applied fields such as reliability, medicine, social sciences, economics, business and criminology. Whereas in life data analysis (LDA) it was assumed that events (failures) were independent and identically distributed (iid), there are many cases where events are dependent and not identically distributed (such as repairable system data) or where the analyst is interested in modeling the number of occurrences of events over time rather than the length of time prior to the first event, as in LDA.

Weibull++ provides both parametric and non-parametric approaches to analyze such data.

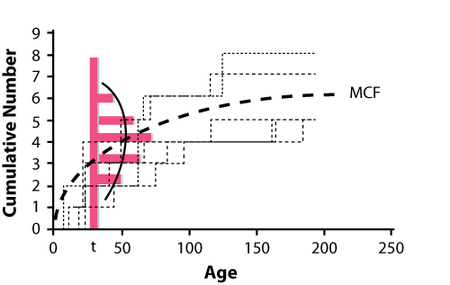
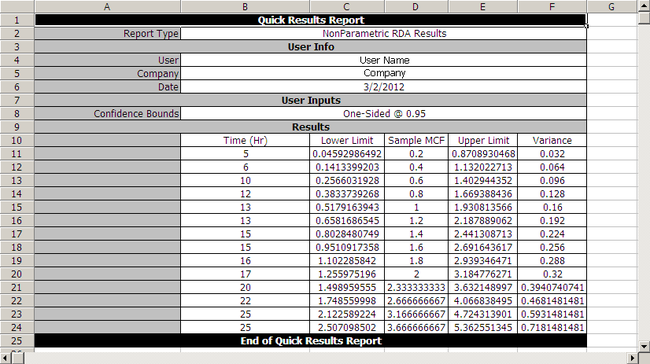
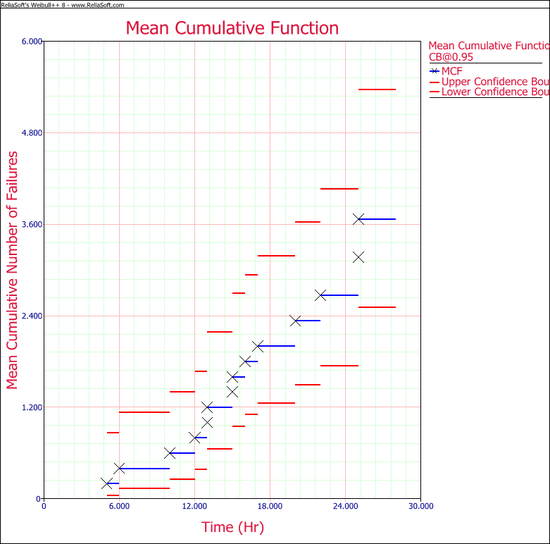
• The non-parametric approach is based on the well-known Mean Cumulative Function (MCF). The Weibull++ module for this type of analysis builds upon the work of Dr. Wayne Nelson, who has written extensively on the calculation and applications of MCF [31].

• The parametric approach is based on the General Renewal Process (GRP) model, which is particularly useful in understanding the effects of the repairs on the age of a system. Traditionally, the commonly used models for analyzing repairable systems data are the perfect renewal processes (PRP), which corresponds to perfect repairs, and the nonhomogeneous Poisson processes (NHPP), which corresponds to minimal repairs. However, most repair activities may realistically not result in such extreme situations but in a complicated intermediate one (general repair or imperfect repair/maintenance), which are well treated with the GRP model.

Parametric Recurrent Event Data Analysis

Weibull++'s parametric RDA folio is a tool for modeling recurrent event data. It can capture the trend, estimate the rate and predict the total number of recurrences. The failure and repair data of a repairable system can be treated as one type of recurrence data. Past and current repairs may affect the future failure process. For most recurrent events, time (distance, cycles, etc.) is a key factor. With time, the recurrence rate may remain constant, increase or decrease. For other recurrent events, not only the time, but also the number of events can affect the recurrence process (e.g., the debugging process in software development).

The parametric analysis approach utilizes the General Renewal Process (GRP) model, as discussed in Mettas and Zhao [28]. In this model, the repair time is assumed to be negligible so that the processes can be viewed as point processes. This model provides a way to describe the rate of occurrence of events over time, such as in the case of data obtained from a repairable system. This model is particularly useful in modeling the failure behavior of a specific system and understanding the effects of the repairs on the age of that system. For example, consider a system that is repaired after a failure, where the repair does not bring the system to an as-good-as-new or an as-bad-as-old condition. In other words, the system is partially rejuvenated after the repair. Traditionally, in as-bad-as-old repairs, also known as minimal repairs, the failure data from such a system would have been modeled using a homogeneous or non-homogeneous Poisson process (NHPP). On rare occasions, a Weibull distribution has been used as well in cases where the system is almost as-good-as-new after the repair, also known as a perfect renewal process (PRP). However, for the intermediate states after the repair, there has not been a commercially available model, even though many models have been proposed in literature. In Weibull++, the GRP model provides the capability to model systems with partial renewal (general repair or imperfect repair/maintenance) and allows for a variety of predictions such as reliability, expected failures, etc.

The GRP Model

In this model, the concept of virtual age is introduced. Let $t_1,t_2,\cdots ,t_n$ represent the successive failure times and let $x_1,x_2,\cdots ,x_n$ represent the time between failures ( $t_i=\sum _{j=1}^i{x}_j)$. Assume that after each event, actions are taken to improve the system performance. Let $q$ be the action effectiveness factor. There are two GRP models:

Type I:

$\begin{array}{r}{v}_i=v_{i-1}+q{x}_i=q{t}_i\end{array}$

Type II:

$v_i=q(v_{i-1}+x_i)=q^i{x}_1+q^{i-1}{x}_2+\cdots +q{x}_i$

where $v_i$ is the virtual age of the system right after $i$th repair. The Type I model assumes that the $i$th repair cannot remove the damage incurred before the $(i-1)$ th repair. It can only reduce the additional age $x_i$ to ${qx}_i$. The Type II model assumes that at the $i$th repair, the virtual age has been accumulated to $v_{i-1}+x_i$. The $i$th repair will remove the cumulative damage from both current and previous failures by reducing the virtual age to $q(v_{i-1}+x_i)$.

The power law function is used to model the rate of recurrence, which is:

$\begin{array}{r}\lambda (t)=\lambda \beta t^{\beta -1}\end{array}$

The conditional pdf is:

$f(t_i|t_{i-1})=\lambda \beta {(x_i+v_{i-1})}^{\beta -1}{e}^{-\lambda [{(x_i+v_{i-1})}^{\beta }-v_{i-1}^{\beta }]}$

MLE method is used to estimate the model parameters. The log likelihood function is discussed in Mettas and Zhao [28]:

$\begin{array}{rl}& \ln (L)=n(\ln \lambda +\ln \beta )-\lambda [{(T-t_n+v_n)}^{\beta }-v_n^{\beta }]\\ & -\lambda \underset{i=1}{\sum ^n}[{(x_i+v_{i-1})}^{\beta }-v_{i-1}^{\beta }]+(\beta -1)\underset{i=1}{\sum ^n}\ln (x_i+v_{i-1})\end{array}$

where $n$ is the total number of events during the entire observation period. $T$ is the stop time of the observation. $T=t_n$ if the observation stops right after the last event.

Confidence Bounds

In general, in order to obtain the virtual age, the exact occurrence time of each event (failure) should be available (see equations for Type I and Type II models). However, the times are unknown until the corresponding events occur. For this reason, there are no closed-form expressions for total failure number and failure intensity, which are functions of failure times and virtual age. Therefore, in Weibull++, a Monte Carlo simulation is used to predict values of virtual time, failure number, MTBF and failure rate. The approximate confidence bounds obtained from simulation are provided. The uncertainty of model parameters is also considered in the bounds.

Bounds on Cumulative Failure (Event) Numbers

The variance of the cumulative failure number $N(t)$ is:

$Var[N(t)]=Var[E(N(t)|\lambda ,\beta ,q)]+E[Var(N(t)|\lambda ,\beta ,q)]$

The first term accounts for the uncertainty of the parameter estimation. The second term considers the uncertainty caused by the renewal process even when model parameters are fixed. However, unless $q=1$ , $Var[E(N(t)|\lambda ,\beta ,q)]$ cannot be calculated because $E(N(t))$ cannot be expressed as a closed-form function of $\lambda ,\beta$, and $q$. In order to consider the uncertainty of the parameter estimation, $Var[E(N(t)|\lambda ,\beta ,q)]$ is approximated by:

$Var[E(N(t)|\lambda ,\beta ,q)]=Var[E(N(v_t)|\lambda ,\beta )]=Var[\lambda v_t^{\beta }]$

where $v_t$ is the expected virtual age at time $t$ and $Var[\lambda v_t^{\beta }]$ is:

$\begin{array}{rlr}& Var[\lambda v_t^{\beta }]=& {\left(\frac{\partial (\lambda v_t^{\beta })}{\partial \beta }\right)}^{2}Var(\hat{\beta })+{\left(\frac{\partial (\lambda v_t^{\beta })}{\partial \lambda }\right)}^{2}Var(\hat{\lambda })\\ & +2\frac{\partial (\lambda v_t^{\beta })}{\partial \beta }\frac{\partial (\lambda v_t^{\beta })}{\partial \lambda }Cov(\hat{\beta },\hat{\lambda })\end{array}$

By conducting this approximation, the uncertainty of $\lambda$ and $\beta$ are considered. The value of $v_t$ and the value of the second term in the equation for the variance of number of failures are obtained through the Monte Carlo simulation using parameters $\hat{\lambda },\hat{\beta },\hat{q},$ which are the ML estimators. The same simulation is used to estimate the cumulative number of failures $\hat{N}(t)=E(N(t)|\hat{\lambda },\hat{\beta },\hat{q})$.

Once the variance and the expected value of $N(t)$ have been obtained, the bounds can be calculated by assuming that $N(t)$ is lognormally distributed as:

$\frac{\ln N(t)-\ln \hat{N}(t)}{\sqrt{Var(\ln N(t))}}\stackrel{~}{}N(0,1)$

The upper and lower bounds for a given confidence level $\alpha$ can be calculated by:

$N{(t)}_{U,L}=\hat{N}(t)e^{\pm z_a\sqrt{Var(N(t))}/\hat{N}(t)}$

where $z_a$ is the standard normal distribution.

If $N(t)$ is assumed to be normally distributed, the bounds can be calculated by:

$N{(t)}_U=\hat{N}(t)+z_a\sqrt{Var(N(t))}$

$N{(t)}_L=\hat{N}(t)-z_a\sqrt{Var(N(t))}$

In Weibull++, the $N(t{)}_U$ is the smaller of the upper bounds obtained from lognormal and normal distribution appoximation. The $N(t{)}_L$ is set to the largest of the lower bounds obtained from lognormal and normal distribution appoximation. This combined method can prevent the out-of-range values of bounds for some small $t$ values.

Bounds of Cumulative Failure Intensity and MTBF

For a given time $t$ , the expected value of cumulative MTBF $m_c(t)$ and cumulative failure intensity ${\lambda }_c(t)$ can be calculated using the following equations:

${\hat{\lambda }}_c(t)=\frac{\hat{N}(t)}{t};{\hat{m}}_c(t)=\frac{t}{\hat{N}(t)}$

The bounds can be easily obtained from the corresponding bounds of $N(t)$.

$\begin{array}{rlr}& {\hat{\lambda }}_c{(t)}_L=& \frac{\hat{N}{(t)}_L}{t};{\hat{\lambda }}_c{(t)}_L=\frac{\hat{N}{(t)}_L}{t};\\ & {\hat{m}}_c{(t)}_L=& \frac{t}{\hat{N}{(t)}_U};{\hat{m}}_c{(t)}_U=\frac{t}{\hat{N}{(t)}_L}\end{array}$

Bounds on Instantaneous Failure Intensity and MTBF

The instantaneous failure intensity is given by:

${\lambda }_i(t)=\lambda \beta v_t^{\beta -1}$

where $v_t$ is the virtual age at time $t$. When $q\ne 1,$ it is obtained from simulation. When $q=1$, $v_t=t$ from model Type I and Type II.

The variance of instantaneous failure intensity can be calculated by:

$\begin{array}{rl}& Var({\lambda }_i(t))={\left(\frac{\partial {\lambda }_i(t)}{\partial \beta }\right)}^{2}Var(\hat{\beta })+{\left(\frac{\partial {\lambda }_i(t)}{\partial \lambda }\right)}^{2}Var(\hat{\lambda })\\ & +2\frac{\partial {\lambda }_i(t)}{\partial \beta }\frac{\partial {\lambda }_i(t)}{\partial \lambda }Cov(\hat{\beta },\hat{\lambda })+{\left(\frac{\partial {\lambda }_i(t)}{\partial v(t)}\right)}^{2}Var({\hat{v}}_t)\end{array}$

The expected value and variance of $v_t$ are obtained from the Monte Carlo simulation with parameters $\hat{\lambda },\hat{\beta },\hat{q}.$ Because of the simulation accuracy and the convergence problem in calculation of $Var(\hat{\beta }),Var(\hat{\lambda })$ and $Cov(\hat{\beta },\hat{\lambda }),$ $Var({\lambda }_i(t))$ can be a negative value at some time points. When this case happens, the bounds of instantaneous failure intensity are not provided.

Once the variance and the expected value of ${\lambda }_i(t)$ are obtained, the bounds can be calculated by assuming that  ${\lambda }_i(t)$ is lognormally distributed as:

$\frac{\ln {\lambda }_i(t)-\ln {\hat{\lambda }}_i(t)}{\sqrt{Var(\ln {\lambda }_i(t))}}\stackrel{~}{}N(0,1)$

The upper and lower bounds for a given confidence level $\alpha$ can be calculated by:

${\lambda }_i(t)={\hat{\lambda }}_i(t)e^{\pm z_a\sqrt{Var({\lambda }_i(t))}/{\hat{\lambda }}_i(t)}$

where $z_a$ is the standard normal distribution.

If ${\lambda }_i(t)$ is assumed to be normally distributed, the bounds can be calculated by:

${\lambda }_i{(t)}_U={\hat{\lambda }}_i(t)+z_a\sqrt{Var(N(t))}$

${\lambda }_i{(t)}_L={\hat{\lambda }}_i(t)-z_a\sqrt{Var(N(t))}$

In Weibull++, ${\lambda }_i(t{)}_U$ is set to the smaller of the two upper bounds obtained from the above lognormal and normal distribution appoximation. ${\lambda }_i(t{)}_L$ is set to the largest of the two lower bounds obtained from the above lognormal and normal distribution appoximation. This combination method can prevent the out of range values of bounds when $t$ values are small.

For a given time $t$, the expected value of cumulative MTBF $m_i(t)$ is:

${\hat{m}}_i(t)=\frac{1}{{\hat{\lambda }}_i(t)}$

The upper and lower bounds can be easily obtained from the corresponding bounds of ${\lambda }_i(t)$:

${\hat{m}}_i{(t)}_U=\frac{1}{{\hat{\lambda }}_i{(t)}_L}$

${\hat{m}}_i{(t)}_L=\frac{1}{{\hat{\lambda }}_i{(t)}_U}$

Bounds on Conditional Reliability

Given mission start time $t_0$ and mission time $T$, the conditional reliability can be calculated by:

$R(T|t_0)=\frac{R(T+v_0)}{R(v_0)}=e^{-\lambda [{(v_0+T)}^{\beta }-v_0]}$

$v_0$ is the virtual age corresponding to time $t_0$. The expected value and the variance of $v_0$ are obtained from Monte Carlo simulation. The variance of the conditional reliability $R(T|t_0)$ is:

$\begin{array}{rl}& Var(R)={\left(\frac{\partial R}{\partial \beta }\right)}^{2}Var(\hat{\beta })+{\left(\frac{\partial R}{\partial \lambda }\right)}^{2}Var(\hat{\lambda })\\ & +2\frac{\partial R}{\partial \beta }\frac{\partial R}{\partial \lambda }Cov(\hat{\beta },\hat{\lambda })+{\left(\frac{\partial R}{\partial v_0}\right)}^{2}Var({\hat{v}}_0)\end{array}$

Because of the simulation accuracy and the convergence problem in calculation of $Var(\hat{\beta }),Var(\hat{\lambda })$ and $Cov(\hat{\beta },\hat{\lambda }),$ $Var(R)$ can be a negative value at some time points. When this case happens, the bounds are not provided.

The bounds are based on:

$\log \text{it}(\hat{R}(T))\stackrel{~}{}N(0,1)$

$\log \text{it}(\hat{R}(T))=\ln \left\{\frac{\hat{R}(T)}{1-\hat{R}(T)}\right\}$

The confidence bounds on reliability are given by:

$R=\frac{\hat{R}}{\hat{R}+(1-\hat{R})e^{\pm \sqrt{Var(R)}/[\hat{R}(1-\hat{R})]}}$

It will be compared with the bounds obtained from:

$R=\hat{R}{e}^{\pm z_a\sqrt{Var(R)}/\hat{R}}$

The smaller of the two upper bounds will be the final upper bound and the larger of the two lower bounds will be the final lower bound.

Example: Air Condition Unit

The following table gives the failure times for the air conditioning unit of an aircraft. The observation ended by the time the last failure occurred, as discussed in Cox [3].

$\begin{array}{ccccc}\text{50}& \text{329}& \text{811}& \text{991}& \text{1489}\\ \text{94}& \text{332}& \text{899}& \text{1013}& \text{1512}\\ \text{196}& \text{347}& \text{945}& \text{1152}& \text{1525}\\ \text{268}& \text{544}& \text{950}& \text{1362}& \text{1539}\\ \text{290}& \text{732}& \text{955}& \text{1459}& \end{array}$

1. Estimate the GRP model parameters using the Type I virtual age option.

2. Plot the failure number and instantaneous failure intensity vs. time with 90% two-sided confidence bounds.

3. Plot the conditional reliability vs. time with 90% two-sided confidence bounds. The mission start time is 40 and mission time is varying.

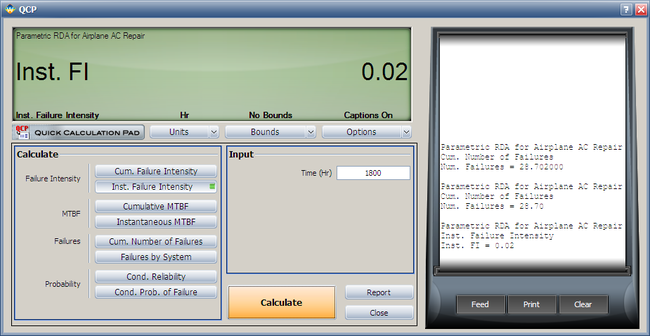
4. Using the QCP, calculate the expected failure number and expected instantaneous failure intensity by time 1800.

Solution

Enter the data into a parametric RDA folio in Weibull++. On the control panel, select the 3 parameters option and the Type I setting. Keep the default simulation settings. Click Calculate.

1. The estimated parameters are $\hat{\beta }=1.1976$, $\hat{\lambda }=4.94E-03$, $\hat{q}=0.1344$.

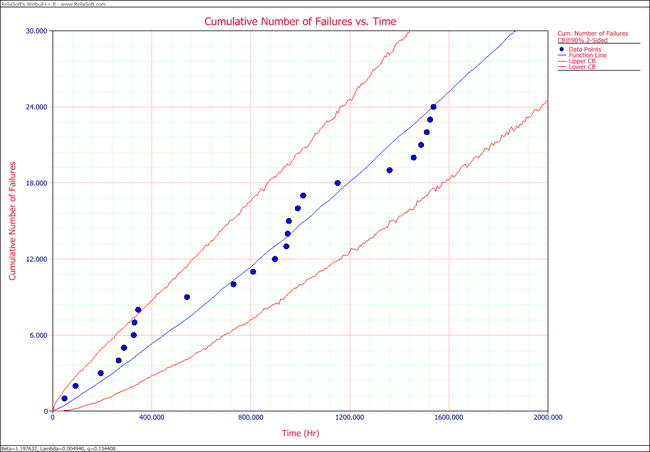
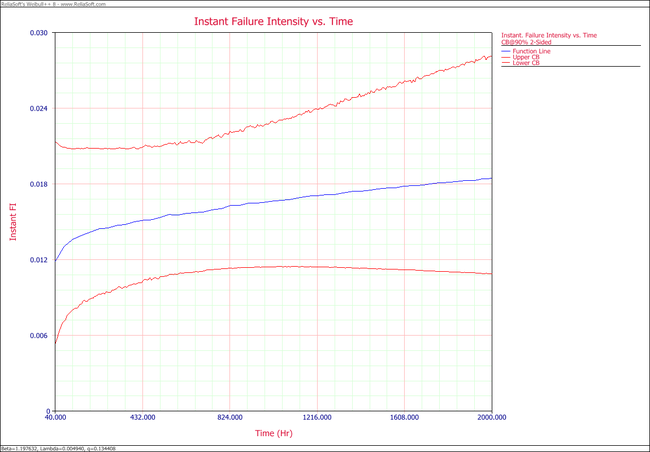
2. The following plots show the cumulative number of failures and instantaneous failure intensity, respectively.

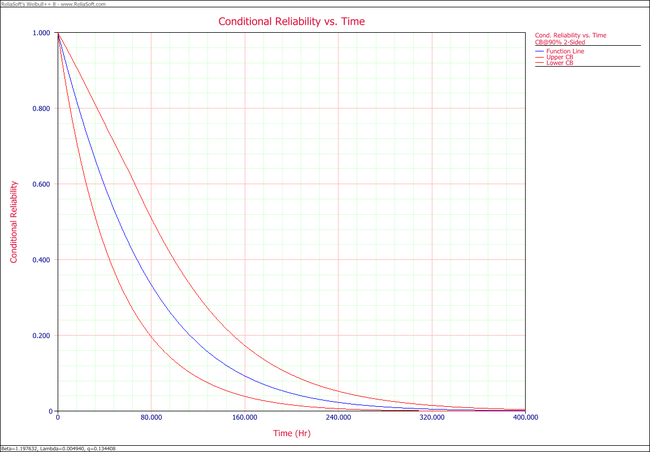
3. The following plot shows the conditional reliability.

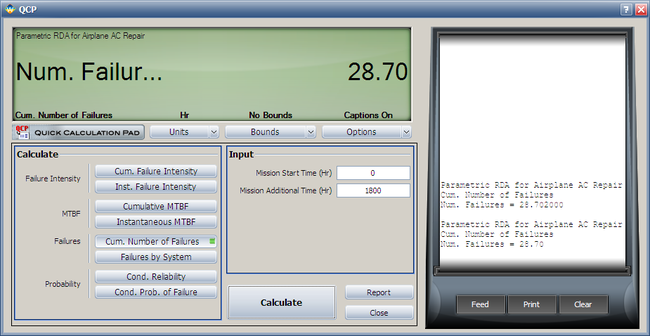
4. Using the QCP, the failure number and instantaneous failure intensity are:

Recurrent Event Data Analysis (RDA) is used in various applied fields such as reliability, medicine, social sciences, economics, business and criminology. Whereas in life data analysis (LDA) it was assumed that events (failures) were independent and identically distributed (iid), there are many cases where events are dependent and not identically distributed (such as repairable system data) or where the analyst is interested in modeling the number of occurrences of events over time rather than the length of time prior to the first event, as in LDA.

Weibull++ provides both parametric and non-parametric approaches to analyze such data.

• The non-parametric approach is based on the well-known Mean Cumulative Function (MCF). The Weibull++ module for this type of analysis builds upon the work of Dr. Wayne Nelson, who has written extensively on the calculation and applications of MCF [31].

• The parametric approach is based on the General Renewal Process (GRP) model, which is particularly useful in understanding the effects of the repairs on the age of a system. Traditionally, the commonly used models for analyzing repairable systems data are the perfect renewal processes (PRP), which corresponds to perfect repairs, and the nonhomogeneous Poisson processes (NHPP), which corresponds to minimal repairs. However, most repair activities may realistically not result in such extreme situations but in a complicated intermediate one (general repair or imperfect repair/maintenance), which are well treated with the GRP model.

Parametric Recurrent Event Data Analysis

Weibull++'s parametric RDA folio is a tool for modeling recurrent event data. It can capture the trend, estimate the rate and predict the total number of recurrences. The failure and repair data of a repairable system can be treated as one type of recurrence data. Past and current repairs may affect the future failure process. For most recurrent events, time (distance, cycles, etc.) is a key factor. With time, the recurrence rate may remain constant, increase or decrease. For other recurrent events, not only the time, but also the number of events can affect the recurrence process (e.g., the debugging process in software development).

The parametric analysis approach utilizes the General Renewal Process (GRP) model, as discussed in Mettas and Zhao [28]. In this model, the repair time is assumed to be negligible so that the processes can be viewed as point processes. This model provides a way to describe the rate of occurrence of events over time, such as in the case of data obtained from a repairable system. This model is particularly useful in modeling the failure behavior of a specific system and understanding the effects of the repairs on the age of that system. For example, consider a system that is repaired after a failure, where the repair does not bring the system to an as-good-as-new or an as-bad-as-old condition. In other words, the system is partially rejuvenated after the repair. Traditionally, in as-bad-as-old repairs, also known as minimal repairs, the failure data from such a system would have been modeled using a homogeneous or non-homogeneous Poisson process (NHPP). On rare occasions, a Weibull distribution has been used as well in cases where the system is almost as-good-as-new after the repair, also known as a perfect renewal process (PRP). However, for the intermediate states after the repair, there has not been a commercially available model, even though many models have been proposed in literature. In Weibull++, the GRP model provides the capability to model systems with partial renewal (general repair or imperfect repair/maintenance) and allows for a variety of predictions such as reliability, expected failures, etc.

The GRP Model

In this model, the concept of virtual age is introduced. Let $t_1,t_2,\cdots ,t_n$ represent the successive failure times and let $x_1,x_2,\cdots ,x_n$ represent the time between failures ( $t_i=\sum _{j=1}^i{x}_j)$. Assume that after each event, actions are taken to improve the system performance. Let $q$ be the action effectiveness factor. There are two GRP models:

Type I:

$\begin{array}{r}{v}_i=v_{i-1}+q{x}_i=q{t}_i\end{array}$

Type II:

$v_i=q(v_{i-1}+x_i)=q^i{x}_1+q^{i-1}{x}_2+\cdots +q{x}_i$

where $v_i$ is the virtual age of the system right after $i$th repair. The Type I model assumes that the $i$th repair cannot remove the damage incurred before the $(i-1)$ th repair. It can only reduce the additional age $x_i$ to ${qx}_i$. The Type II model assumes that at the $i$th repair, the virtual age has been accumulated to $v_{i-1}+x_i$. The $i$th repair will remove the cumulative damage from both current and previous failures by reducing the virtual age to $q(v_{i-1}+x_i)$.

The power law function is used to model the rate of recurrence, which is:

$\begin{array}{r}\lambda (t)=\lambda \beta t^{\beta -1}\end{array}$

The conditional pdf is:

$f(t_i|t_{i-1})=\lambda \beta {(x_i+v_{i-1})}^{\beta -1}{e}^{-\lambda [{(x_i+v_{i-1})}^{\beta }-v_{i-1}^{\beta }]}$

MLE method is used to estimate the model parameters. The log likelihood function is discussed in Mettas and Zhao [28]:

$\begin{array}{rl}& \ln (L)=n(\ln \lambda +\ln \beta )-\lambda [{(T-t_n+v_n)}^{\beta }-v_n^{\beta }]\\ & -\lambda \underset{i=1}{\sum ^n}[{(x_i+v_{i-1})}^{\beta }-v_{i-1}^{\beta }]+(\beta -1)\underset{i=1}{\sum ^n}\ln (x_i+v_{i-1})\end{array}$

where $n$ is the total number of events during the entire observation period. $T$ is the stop time of the observation. $T=t_n$ if the observation stops right after the last event.

Confidence Bounds

In general, in order to obtain the virtual age, the exact occurrence time of each event (failure) should be available (see equations for Type I and Type II models). However, the times are unknown until the corresponding events occur. For this reason, there are no closed-form expressions for total failure number and failure intensity, which are functions of failure times and virtual age. Therefore, in Weibull++, a Monte Carlo simulation is used to predict values of virtual time, failure number, MTBF and failure rate. The approximate confidence bounds obtained from simulation are provided. The uncertainty of model parameters is also considered in the bounds.

Bounds on Cumulative Failure (Event) Numbers

The variance of the cumulative failure number $N(t)$ is:

$Var[N(t)]=Var[E(N(t)|\lambda ,\beta ,q)]+E[Var(N(t)|\lambda ,\beta ,q)]$

The first term accounts for the uncertainty of the parameter estimation. The second term considers the uncertainty caused by the renewal process even when model parameters are fixed. However, unless $q=1$ , $Var[E(N(t)|\lambda ,\beta ,q)]$ cannot be calculated because $E(N(t))$ cannot be expressed as a closed-form function of $\lambda ,\beta$, and $q$. In order to consider the uncertainty of the parameter estimation, $Var[E(N(t)|\lambda ,\beta ,q)]$ is approximated by:

$Var[E(N(t)|\lambda ,\beta ,q)]=Var[E(N(v_t)|\lambda ,\beta )]=Var[\lambda v_t^{\beta }]$

where $v_t$ is the expected virtual age at time $t$ and $Var[\lambda v_t^{\beta }]$ is:

$\begin{array}{rlr}& Var[\lambda v_t^{\beta }]=& {\left(\frac{\partial (\lambda v_t^{\beta })}{\partial \beta }\right)}^{2}Var(\hat{\beta })+{\left(\frac{\partial (\lambda v_t^{\beta })}{\partial \lambda }\right)}^{2}Var(\hat{\lambda })\\ & +2\frac{\partial (\lambda v_t^{\beta })}{\partial \beta }\frac{\partial (\lambda v_t^{\beta })}{\partial \lambda }Cov(\hat{\beta },\hat{\lambda })\end{array}$

By conducting this approximation, the uncertainty of $\lambda$ and $\beta$ are considered. The value of $v_t$ and the value of the second term in the equation for the variance of number of failures are obtained through the Monte Carlo simulation using parameters $\hat{\lambda },\hat{\beta },\hat{q},$ which are the ML estimators. The same simulation is used to estimate the cumulative number of failures $\hat{N}(t)=E(N(t)|\hat{\lambda },\hat{\beta },\hat{q})$.

Once the variance and the expected value of $N(t)$ have been obtained, the bounds can be calculated by assuming that $N(t)$ is lognormally distributed as:

$\frac{\ln N(t)-\ln \hat{N}(t)}{\sqrt{Var(\ln N(t))}}\stackrel{~}{}N(0,1)$

The upper and lower bounds for a given confidence level $\alpha$ can be calculated by:

$N{(t)}_{U,L}=\hat{N}(t)e^{\pm z_a\sqrt{Var(N(t))}/\hat{N}(t)}$

where $z_a$ is the standard normal distribution.

If $N(t)$ is assumed to be normally distributed, the bounds can be calculated by:

$N{(t)}_U=\hat{N}(t)+z_a\sqrt{Var(N(t))}$

$N{(t)}_L=\hat{N}(t)-z_a\sqrt{Var(N(t))}$

In Weibull++, the $N(t{)}_U$ is the smaller of the upper bounds obtained from lognormal and normal distribution appoximation. The $N(t{)}_L$ is set to the largest of the lower bounds obtained from lognormal and normal distribution appoximation. This combined method can prevent the out-of-range values of bounds for some small $t$ values.

Bounds of Cumulative Failure Intensity and MTBF

For a given time $t$ , the expected value of cumulative MTBF $m_c(t)$ and cumulative failure intensity ${\lambda }_c(t)$ can be calculated using the following equations:

${\hat{\lambda }}_c(t)=\frac{\hat{N}(t)}{t};{\hat{m}}_c(t)=\frac{t}{\hat{N}(t)}$

The bounds can be easily obtained from the corresponding bounds of $N(t)$.

$\begin{array}{rlr}& {\hat{\lambda }}_c{(t)}_L=& \frac{\hat{N}{(t)}_L}{t};{\hat{\lambda }}_c{(t)}_L=\frac{\hat{N}{(t)}_L}{t};\\ & {\hat{m}}_c{(t)}_L=& \frac{t}{\hat{N}{(t)}_U};{\hat{m}}_c{(t)}_U=\frac{t}{\hat{N}{(t)}_L}\end{array}$

Bounds on Instantaneous Failure Intensity and MTBF

The instantaneous failure intensity is given by:

${\lambda }_i(t)=\lambda \beta v_t^{\beta -1}$

where $v_t$ is the virtual age at time $t$. When $q\ne 1,$ it is obtained from simulation. When $q=1$, $v_t=t$ from model Type I and Type II.

The variance of instantaneous failure intensity can be calculated by:

$\begin{array}{rl}& Var({\lambda }_i(t))={\left(\frac{\partial {\lambda }_i(t)}{\partial \beta }\right)}^{2}Var(\hat{\beta })+{\left(\frac{\partial {\lambda }_i(t)}{\partial \lambda }\right)}^{2}Var(\hat{\lambda })\\ & +2\frac{\partial {\lambda }_i(t)}{\partial \beta }\frac{\partial {\lambda }_i(t)}{\partial \lambda }Cov(\hat{\beta },\hat{\lambda })+{\left(\frac{\partial {\lambda }_i(t)}{\partial v(t)}\right)}^{2}Var({\hat{v}}_t)\end{array}$

The expected value and variance of $v_t$ are obtained from the Monte Carlo simulation with parameters $\hat{\lambda },\hat{\beta },\hat{q}.$ Because of the simulation accuracy and the convergence problem in calculation of $Var(\hat{\beta }),Var(\hat{\lambda })$ and $Cov(\hat{\beta },\hat{\lambda }),$ $Var({\lambda }_i(t))$ can be a negative value at some time points. When this case happens, the bounds of instantaneous failure intensity are not provided.

Once the variance and the expected value of ${\lambda }_i(t)$ are obtained, the bounds can be calculated by assuming that  ${\lambda }_i(t)$ is lognormally distributed as:

$\frac{\ln {\lambda }_i(t)-\ln {\hat{\lambda }}_i(t)}{\sqrt{Var(\ln {\lambda }_i(t))}}\stackrel{~}{}N(0,1)$

The upper and lower bounds for a given confidence level $\alpha$ can be calculated by:

${\lambda }_i(t)={\hat{\lambda }}_i(t)e^{\pm z_a\sqrt{Var({\lambda }_i(t))}/{\hat{\lambda }}_i(t)}$

where $z_a$ is the standard normal distribution.

If ${\lambda }_i(t)$ is assumed to be normally distributed, the bounds can be calculated by:

${\lambda }_i{(t)}_U={\hat{\lambda }}_i(t)+z_a\sqrt{Var(N(t))}$

${\lambda }_i{(t)}_L={\hat{\lambda }}_i(t)-z_a\sqrt{Var(N(t))}$

In Weibull++, ${\lambda }_i(t{)}_U$ is set to the smaller of the two upper bounds obtained from the above lognormal and normal distribution appoximation. ${\lambda }_i(t{)}_L$ is set to the largest of the two lower bounds obtained from the above lognormal and normal distribution appoximation. This combination method can prevent the out of range values of bounds when $t$ values are small.

For a given time $t$, the expected value of cumulative MTBF $m_i(t)$ is:

${\hat{m}}_i(t)=\frac{1}{{\hat{\lambda }}_i(t)}$

The upper and lower bounds can be easily obtained from the corresponding bounds of ${\lambda }_i(t)$:

${\hat{m}}_i{(t)}_U=\frac{1}{{\hat{\lambda }}_i{(t)}_L}$

${\hat{m}}_i{(t)}_L=\frac{1}{{\hat{\lambda }}_i{(t)}_U}$

Bounds on Conditional Reliability

Given mission start time $t_0$ and mission time $T$, the conditional reliability can be calculated by:

$R(T|t_0)=\frac{R(T+v_0)}{R(v_0)}=e^{-\lambda [{(v_0+T)}^{\beta }-v_0]}$

$v_0$ is the virtual age corresponding to time $t_0$. The expected value and the variance of $v_0$ are obtained from Monte Carlo simulation. The variance of the conditional reliability $R(T|t_0)$ is:

$\begin{array}{rl}& Var(R)={\left(\frac{\partial R}{\partial \beta }\right)}^{2}Var(\hat{\beta })+{\left(\frac{\partial R}{\partial \lambda }\right)}^{2}Var(\hat{\lambda })\\ & +2\frac{\partial R}{\partial \beta }\frac{\partial R}{\partial \lambda }Cov(\hat{\beta },\hat{\lambda })+{\left(\frac{\partial R}{\partial v_0}\right)}^{2}Var({\hat{v}}_0)\end{array}$

Because of the simulation accuracy and the convergence problem in calculation of $Var(\hat{\beta }),Var(\hat{\lambda })$ and $Cov(\hat{\beta },\hat{\lambda }),$ $Var(R)$ can be a negative value at some time points. When this case happens, the bounds are not provided.

The bounds are based on:

$\log \text{it}(\hat{R}(T))\stackrel{~}{}N(0,1)$

$\log \text{it}(\hat{R}(T))=\ln \left\{\frac{\hat{R}(T)}{1-\hat{R}(T)}\right\}$

The confidence bounds on reliability are given by:

$R=\frac{\hat{R}}{\hat{R}+(1-\hat{R})e^{\pm \sqrt{Var(R)}/[\hat{R}(1-\hat{R})]}}$

It will be compared with the bounds obtained from:

$R=\hat{R}{e}^{\pm z_a\sqrt{Var(R)}/\hat{R}}$

The smaller of the two upper bounds will be the final upper bound and the larger of the two lower bounds will be the final lower bound.

Example: Air Condition Unit

The following table gives the failure times for the air conditioning unit of an aircraft. The observation ended by the time the last failure occurred, as discussed in Cox [3].

$\begin{array}{ccccc}\text{50}& \text{329}& \text{811}& \text{991}& \text{1489}\\ \text{94}& \text{332}& \text{899}& \text{1013}& \text{1512}\\ \text{196}& \text{347}& \text{945}& \text{1152}& \text{1525}\\ \text{268}& \text{544}& \text{950}& \text{1362}& \text{1539}\\ \text{290}& \text{732}& \text{955}& \text{1459}& \end{array}$

1. Estimate the GRP model parameters using the Type I virtual age option.

2. Plot the failure number and instantaneous failure intensity vs. time with 90% two-sided confidence bounds.

3. Plot the conditional reliability vs. time with 90% two-sided confidence bounds. The mission start time is 40 and mission time is varying.

4. Using the QCP, calculate the expected failure number and expected instantaneous failure intensity by time 1800.

Solution

Enter the data into a parametric RDA folio in Weibull++. On the control panel, select the 3 parameters option and the Type I setting. Keep the default simulation settings. Click Calculate.

1. The estimated parameters are $\hat{\beta }=1.1976$, $\hat{\lambda }=4.94E-03$, $\hat{q}=0.1344$.

2. The following plots show the cumulative number of failures and instantaneous failure intensity, respectively.

3. The following plot shows the conditional reliability.

4. Using the QCP, the failure number and instantaneous failure intensity are: