Difference Detection Matrix Example
Test Design Using Life Difference Detection Matrix
Assume there are two design options for a new product. Engineers need to design a test to compare the reliability performance of these two options. Both designs are assumed following Weibull distribution. For Design 1, its shape parameter [math]\displaystyle{ \beta }[/math] = 3; for Design 2, its [math]\displaystyle{ \beta }[/math] = 2. Their B10 lives may range from 500 to 3,000 hours. We want to use the Difference Detection Matrix to choose the suitable sample size and test duration.
Solution
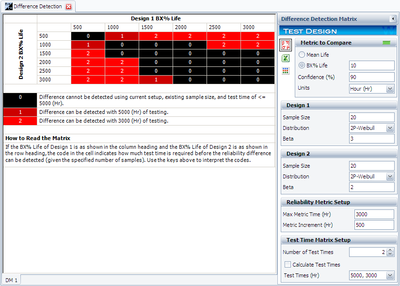
Initially, the sample size for each design is set to 20. Two test durations 3,000 and 5,000 also were chosen. Based on these settings and the assumptions on the failure time distributions, the following Difference Detection Matrix is obtained.
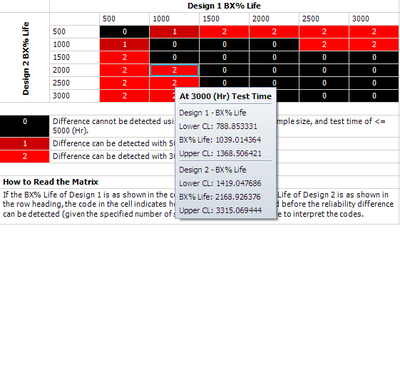
In the above figure, the range of the assumed B10 life for each design is from 500 to 3,000. The pair-wised comparison results are displayed in each cell. 0 means the difference cannot be detected through the test; 1 means the difference can be detected if the test duration is 5,000 hours; 2 means the difference can be detected if the test duration is 3,000 hours. For example for cell (1000, 2000), the number is 2. It means if the B10 life for design 1 is 1,000 hours and the B10 life for design 2 is 2,000 hours. the difference can be detected if the test duration is at least 5,000 hours. By testing 20 samples each for 3,000 hours, the difference of their B10 lives probably can be detected. This is because at a confidence level of 90%, their estimated confidence intervals of the B10 life do not overlap. The estimated intervals can be seen in the figure below.
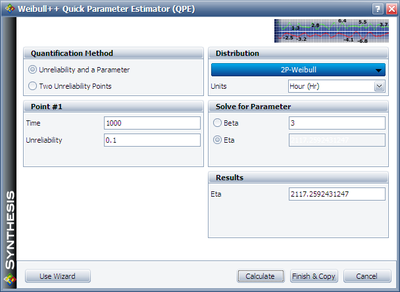
We will use design 1 to illustrate how the interval is calculated. Since for cell (1000, 2000), design 1's B10 life is 1,000 and the assumed [math]\displaystyle{ \beta }[/math] is 3, we can calculate the [math]\displaystyle{ \eta }[/math] for the Weibull distribution using the Quick Parameter Estimator tool. This is given in the next figure.
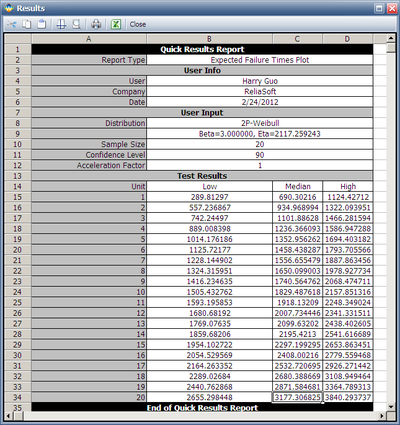
The estimated [math]\displaystyle{ \eta }[/math] is 2117.2592. Then we can use these distribution parameters and sample size of 20 to get the expected failure times using the Expected Failure Times Plot as shown below.
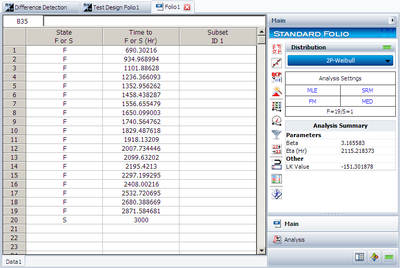
The median failure times are used to estimated the failure distribution. Please notice that since the test duration is set to 3,000 hours, any failures occurred after 3,000 is set to suspensions. In this case, the last failure is a suspension with suspension time of 3,000. Now we can enter these data into a standard Weibull++ folio as given in the next figure.
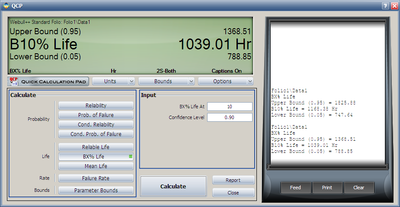
Please make sure the MLE and FM options are selected. Use the estimated results, we can calculate the B10 life and its interval in QCP, as given in below.
From the above result, we can see the estimated B10 life and its interval are the same as the results displayed in the Difference Detection Matrix.
For design 2 and other cells, the above procedure can be repeated to get the results. Therefore, by adjusting the sample size and test duration, a suitable test for detecting a certain amount of difference of two designs/populations can be identified.