Template:Alta ld
The Lognormal Distribution
The lognormal distribution is commonly used for general reliability analysis, cycles-to-failure in fatigue, material strengths and loading variables in probabilistic design. A random variable is lognormally distributed if the logarithm of the random variable is normally distributed. Since the logarithms of a lognormally distributed random variable are normally distributed, the lognormal distribution is given by:
- where:
- •
- •
- •
The lognormal
Taking the derivative yields:
Substitution yields:
- where:
In this chapter, we will briefly present three lifetime distributions commonly used in accelerated life test analysis: the exponential, the Weibull and the lognormal distributions. Note that although all forms are mentioned below, ALTA uses the 1-parameter form of the exponential distribution and the 2-parameter form of the Weibull distribution.
Readers who are interested in a more rigorous overview of these distributions (or for information about other life distributions) can refer to the Life data analysis reference. For information about the parameter estimation methods, see Appendix B.
The Exponential Distribution
The exponential distribution is commonly used for components or systems exhibiting a constant failure rate. Due to its simplicity, it has been widely employed, even in cases where it doesn't apply. In its most general case, the 2-parameter exponential distribution is defined by:
Where
If the location parameter,
For a detailed discussion of this distribution, see The Exponential Distribution.
Exponential Distribution Functions
The Mean or MTTF
The mean,
Note that when
The Median
The median,
The Mode
The mode,
The Standard Deviation
The standard deviation,
The Exponential Reliability Function
The equation for the 2-parameter exponential cumulative density function, or cdf, is given by:
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function of the 2-parameter exponential distribution is given by:
The 1-parameter exponential reliability function is given by:
The Exponential Conditional Reliability Function
The exponential conditional reliability equation gives the reliability for a mission of
which says that the reliability for a mission of
The Exponential Reliable Life Function
The reliable life, or the mission duration for a desired reliability goal,
or:
The Exponential Failure Rate Function
The exponential failure rate function is:
Once again, note that the constant failure rate is a characteristic of the exponential distribution, and special cases of other distributions only. Most other distributions have failure rates that are functions of time.
Characteristics of the Exponential Distribution
The primary trait of the exponential distribution is that it is used for modeling the behavior of items with a constant failure rate. It has a fairly simple mathematical form, which makes it fairly easy to manipulate. Unfortunately, this fact also leads to the use of this model in situations where it is not appropriate. For example, it would not be appropriate to use the exponential distribution to model the reliability of an automobile. The constant failure rate of the exponential distribution would require the assumption that the automobile would be just as likely to experience a breakdown during the first mile as it would during the one-hundred-thousandth mile. Clearly, this is not a valid assumption. However, some inexperienced practitioners of reliability engineering and life data analysis will overlook this fact, lured by the siren-call of the exponential distribution's relatively simple mathematical models.
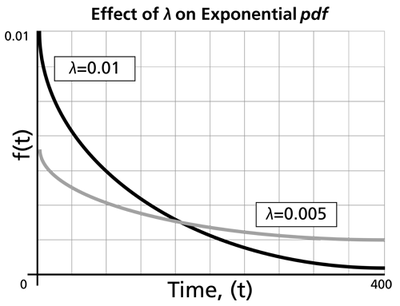
The Effect of lambda and gamma on the Exponential pdf
- The exponential pdf has no shape parameter, as it has only one shape.
- The exponential pdf is always convex and is stretched to the right as
- The value of the pdf function is always equal to the value of
- The location parameter,
- The scale parameter is
- As
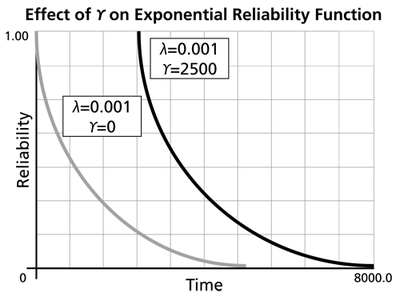
The Effect of lambda and gamma on the Exponential Reliability Function
- The 1-parameter exponential reliability function starts at the value of 100% at
- The 2-parameter exponential reliability function remains at the value of 100% for
- As
- The reliability for a mission duration of
- The 1-parameter exponential reliability function starts at the value of 100% at
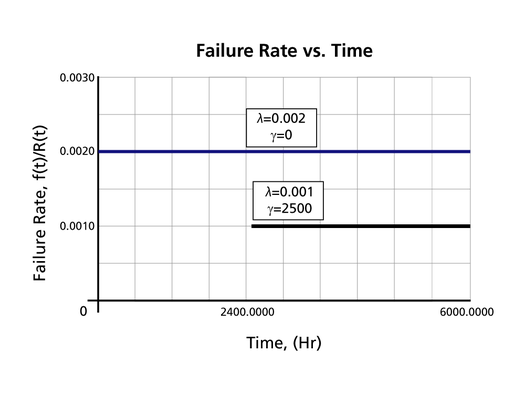
The Effect of lambda and gamma on the Failure Rate Function
- The 1-parameter exponential failure rate function is constant and starts at
- The 2-parameter exponential failure rate function remains at the value of 0 for
- The 1-parameter exponential failure rate function is constant and starts at
The Weibull Distribution
The Weibull distribution is a general purpose reliability distribution used to model material strength, times-to-failure of electronic and mechanical components, equipment or systems. In its most general case, the 3-parameter Weibull pdf is defined by:
where
If the location parameter,
One additional form is the 1-parameter Weibull distribution, which assumes that the location parameter,
For a detailed discussion of this distribution, see The Weibull Distribution.
Weibull Distribution Functions
The Mean or MTTF
The mean,
where
is the gamma function evaluated at the value of:
The gamma function is defined as:
For the 2-parameter case, this can be reduced to:
Note that some practitioners erroneously assume that
The Median
The median,
The Mode
The mode,
The Standard Deviation
The standard deviation,
The Weibull Reliability Function
The equation for the 3-parameter Weibull cumulative density function, cdf, is given by:
This is also referred to as unreliability and designated as
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function for the 3-parameter Weibull distribution is then given by:
The Weibull Conditional Reliability Function
The 3-parameter Weibull conditional reliability function is given by:
or:
These give the reliability for a new mission of
The Weibull Reliable Life
The reliable life,
This is the life for which the unit/item will be functioning successfully with a reliability of
The Weibull Failure Rate Function
The Weibull failure rate function,
Characteristics of the Weibull Distribution
The Weibull distribution is widely used in reliability and life data analysis due to its versatility. Depending on the values of the parameters, the Weibull distribution can be used to model a variety of life behaviors. We will now examine how the values of the shape parameter,
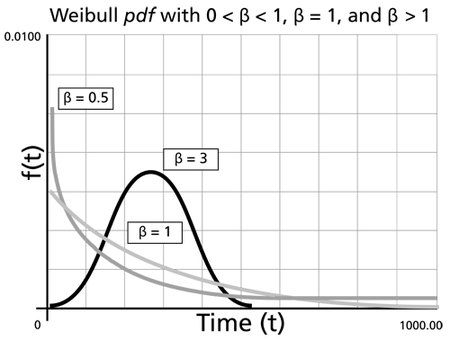
Effects of the Shape Parameter, beta
The Weibull shape parameter,
where
For
- As
- As
- The mode is non-existent.
- As
For
- For
The Effect of beta on the cdf and Reliability Function
The above figure shows the effect of the value of
- For
- For
The Effect of beta on the Weibull Failure Rate
The value of
As indicated by above figure, populations with
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units.
For
For
When
Effects of the Scale Parameter, eta
A change in the scale parameter
- If
- If
- If
Effects of the Location Parameter, gamma
The location parameter,
- When
- If
- If
- The life period 0 to
- The parameter
- When
The Lognormal Distribution
The lognormal distribution is commonly used for general reliability analysis, cycles-to-failure in fatigue, material strengths and loading variables in probabilistic design. When the natural logarithms of the times-to-failure are normally distributed, then we say that the data follow the lognormal distribution.
The pdf of the lognormal distribution is given by:
where
For a detailed discussion of this distribution, see The Lognormal Distribution.
Lognormal Distribution Functions
The Mean or MTTF
The mean of the lognormal distribution,
The mean of the natural logarithms of the times-to-failure,
The Median
The median of the lognormal distribution,
The Mode
The mode of the lognormal distribution,
The Standard Deviation
The standard deviation of the lognormal distribution,
The standard deviation of the natural logarithms of the times-to-failure,
The Lognormal Reliability Function
The reliability for a mission of time
or:
As with the normal distribution, there is no closed-form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables. Since the application automatically solves for the reliability we will not discuss manual solution methods. For interested readers, full explanations can be found in the references.
The Lognormal Conditional Reliability Function
The lognormal conditional reliability function is given by:
Once again, the use of standard normal tables is necessary to solve this equation, as no closed-form solution exists.
The Lognormal Reliable Life Function
As there is no closed-form solution for the lognormal reliability equation, no closed-form solution exists for the lognormal reliable life either. In order to determine this value, one must solve the following equation for
The Lognormal Failure Rate Function
The lognormal failure rate is given by:
As with the reliability equations, standard normal tables will be required to solve for this function.
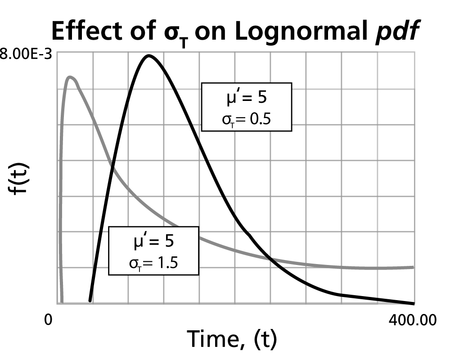
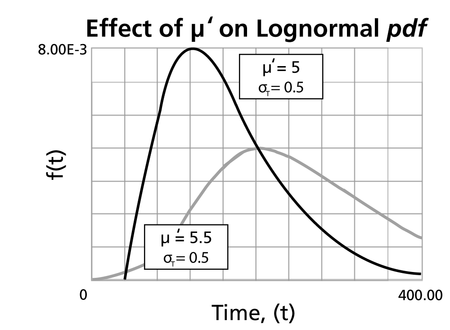
Characteristics of the Lognormal Distribution
- The lognormal distribution is a distribution skewed to the right.
- The pdf starts at zero, increases to its mode, and decreases thereafter.
- The degree of skewness increases as
- For the same
- For
- The parameter,
- The parameter
Lognormal Distribution Parameters in ReliaSoft's Software
In ReliaSoft's software, the parameters returned for the lognormal distribution are always logarithmic. That is: the parameter
In this chapter, we will briefly present three lifetime distributions commonly used in accelerated life test analysis: the exponential, the Weibull and the lognormal distributions. Note that although all forms are mentioned below, ALTA uses the 1-parameter form of the exponential distribution and the 2-parameter form of the Weibull distribution.
Readers who are interested in a more rigorous overview of these distributions (or for information about other life distributions) can refer to the Life data analysis reference. For information about the parameter estimation methods, see Appendix B.
The Exponential Distribution
The exponential distribution is commonly used for components or systems exhibiting a constant failure rate. Due to its simplicity, it has been widely employed, even in cases where it doesn't apply. In its most general case, the 2-parameter exponential distribution is defined by:
Where
If the location parameter,
For a detailed discussion of this distribution, see The Exponential Distribution.
Exponential Distribution Functions
The Mean or MTTF
The mean,
Note that when
The Median
The median,
The Mode
The mode,
The Standard Deviation
The standard deviation,
The Exponential Reliability Function
The equation for the 2-parameter exponential cumulative density function, or cdf, is given by:
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function of the 2-parameter exponential distribution is given by:
The 1-parameter exponential reliability function is given by:
The Exponential Conditional Reliability Function
The exponential conditional reliability equation gives the reliability for a mission of
which says that the reliability for a mission of
The Exponential Reliable Life Function
The reliable life, or the mission duration for a desired reliability goal,
or:
The Exponential Failure Rate Function
The exponential failure rate function is:
Once again, note that the constant failure rate is a characteristic of the exponential distribution, and special cases of other distributions only. Most other distributions have failure rates that are functions of time.
Characteristics of the Exponential Distribution
The primary trait of the exponential distribution is that it is used for modeling the behavior of items with a constant failure rate. It has a fairly simple mathematical form, which makes it fairly easy to manipulate. Unfortunately, this fact also leads to the use of this model in situations where it is not appropriate. For example, it would not be appropriate to use the exponential distribution to model the reliability of an automobile. The constant failure rate of the exponential distribution would require the assumption that the automobile would be just as likely to experience a breakdown during the first mile as it would during the one-hundred-thousandth mile. Clearly, this is not a valid assumption. However, some inexperienced practitioners of reliability engineering and life data analysis will overlook this fact, lured by the siren-call of the exponential distribution's relatively simple mathematical models.
The Effect of lambda and gamma on the Exponential pdf
- The exponential pdf has no shape parameter, as it has only one shape.
- The exponential pdf is always convex and is stretched to the right as
- The value of the pdf function is always equal to the value of
- The location parameter,
- The scale parameter is
- As
The Effect of lambda and gamma on the Exponential Reliability Function
- The 1-parameter exponential reliability function starts at the value of 100% at
- The 2-parameter exponential reliability function remains at the value of 100% for
- As
- The reliability for a mission duration of
- The 1-parameter exponential reliability function starts at the value of 100% at
The Effect of lambda and gamma on the Failure Rate Function
- The 1-parameter exponential failure rate function is constant and starts at
- The 2-parameter exponential failure rate function remains at the value of 0 for
- The 1-parameter exponential failure rate function is constant and starts at
The Weibull Distribution
The Weibull distribution is a general purpose reliability distribution used to model material strength, times-to-failure of electronic and mechanical components, equipment or systems. In its most general case, the 3-parameter Weibull pdf is defined by:
where
If the location parameter,
One additional form is the 1-parameter Weibull distribution, which assumes that the location parameter,
For a detailed discussion of this distribution, see The Weibull Distribution.
Weibull Distribution Functions
The Mean or MTTF
The mean,
where
is the gamma function evaluated at the value of:
The gamma function is defined as:
For the 2-parameter case, this can be reduced to:
Note that some practitioners erroneously assume that
The Median
The median,
The Mode
The mode,
The Standard Deviation
The standard deviation,
The Weibull Reliability Function
The equation for the 3-parameter Weibull cumulative density function, cdf, is given by:
This is also referred to as unreliability and designated as
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function for the 3-parameter Weibull distribution is then given by:
The Weibull Conditional Reliability Function
The 3-parameter Weibull conditional reliability function is given by:
or:
These give the reliability for a new mission of
The Weibull Reliable Life
The reliable life,
This is the life for which the unit/item will be functioning successfully with a reliability of
The Weibull Failure Rate Function
The Weibull failure rate function,
Characteristics of the Weibull Distribution
The Weibull distribution is widely used in reliability and life data analysis due to its versatility. Depending on the values of the parameters, the Weibull distribution can be used to model a variety of life behaviors. We will now examine how the values of the shape parameter,
Effects of the Shape Parameter, beta
The Weibull shape parameter,
where
For
- As
- As
- The mode is non-existent.
- As
For
- For
The Effect of beta on the cdf and Reliability Function
The above figure shows the effect of the value of
- For
- For
The Effect of beta on the Weibull Failure Rate
The value of
As indicated by above figure, populations with
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units.
For
For
When
Effects of the Scale Parameter, eta
A change in the scale parameter
- If
- If
- If
Effects of the Location Parameter, gamma
The location parameter,
- When
- If
- If
- The life period 0 to
- The parameter
- When
The Lognormal Distribution
The lognormal distribution is commonly used for general reliability analysis, cycles-to-failure in fatigue, material strengths and loading variables in probabilistic design. When the natural logarithms of the times-to-failure are normally distributed, then we say that the data follow the lognormal distribution.
The pdf of the lognormal distribution is given by:
where
For a detailed discussion of this distribution, see The Lognormal Distribution.
Lognormal Distribution Functions
The Mean or MTTF
The mean of the lognormal distribution,
The mean of the natural logarithms of the times-to-failure,
The Median
The median of the lognormal distribution,
The Mode
The mode of the lognormal distribution,
The Standard Deviation
The standard deviation of the lognormal distribution,
The standard deviation of the natural logarithms of the times-to-failure,
The Lognormal Reliability Function
The reliability for a mission of time
or:
As with the normal distribution, there is no closed-form solution for the lognormal reliability function. Solutions can be obtained via the use of standard normal tables. Since the application automatically solves for the reliability we will not discuss manual solution methods. For interested readers, full explanations can be found in the references.
The Lognormal Conditional Reliability Function
The lognormal conditional reliability function is given by:
Once again, the use of standard normal tables is necessary to solve this equation, as no closed-form solution exists.
The Lognormal Reliable Life Function
As there is no closed-form solution for the lognormal reliability equation, no closed-form solution exists for the lognormal reliable life either. In order to determine this value, one must solve the following equation for
The Lognormal Failure Rate Function
The lognormal failure rate is given by:
As with the reliability equations, standard normal tables will be required to solve for this function.
Characteristics of the Lognormal Distribution
- The lognormal distribution is a distribution skewed to the right.
- The pdf starts at zero, increases to its mode, and decreases thereafter.
- The degree of skewness increases as
- For the same
- For
- The parameter,
- The parameter
Lognormal Distribution Parameters in ReliaSoft's Software
In ReliaSoft's software, the parameters returned for the lognormal distribution are always logarithmic. That is: the parameter
Parameter Estimation
The estimate of the parameters of the lognormal distribution can be found graphically on probability plotting paper or analytically using either least squares or maximum likelihood. (Parameter estimation methods are presented in detail in Appendix B.)
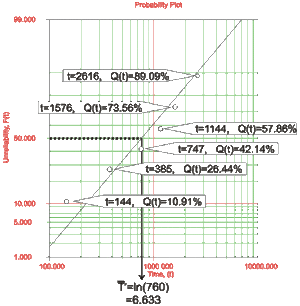
Example 5
Let's assume six identical units are being reliability tested at the same application and operation stress levels. All of these units fail during the test after operating the following times (in hours),
- • Rank the times-to-failure in ascending order as shown next.
- • Obtain their median rank plotting positions. The times-to-failure, with their corresponding median ranks, are shown next:
- • On a lognormal probability paper, plot the times and their corresponding rank value. The next figure displays an example of a lognormal probability paper. The paper is simply a log-log paper.
- • Draw the best possible straight line that goes through the
and
- • At the
- • The standard deviation,
Now any reliability value for any mission time
To obtain the value from the plot, draw a vertical line from the abscissa, at
MLE Parameter Estimation
The parameters of the lognormal distribution can also be estimated using maximum likelihood estimation (MLE). This general log-likelihood function is:
where:
and:
The solution will be found by solving for a pair of parameters
and:
Example 6
Using the same data as in the probability plotting example (Example 5), and assuming a lognormal distribution, estimate the parameters using the MLE method.
Solution
In this example we have non-grouped data without suspensions. Thus, the partials reduce to:
Substituting the values of
The mean and standard deviation of the times-to-failure can be estimated using Eqns. (mean) and (sdv):
- and:
| The material on this page is copyrighted. | ©1992-2012. ReliaSoft Corporation. ALL RIGHTS RESERVED. |
[[Category:Acclerated_Testing_Reference]

![Effect on [math]\displaystyle{ \beta\,\! }[/math] on the cdf on the Weibull probability plot with a fixed value of [math]\displaystyle{ \eta\,\! }[/math]](/images/b/bf/WB.8_effect_of_weibull.png)
![The effect of values of [math]\displaystyle{ \beta\,\! }[/math] on the Weibull reliability plot.](/images/0/0c/WB.8_weibull_reliability.png)
![The effect of [math]\displaystyle{ \beta\,\! }[/math] on the Weibull failure rate function.](/images/9/9c/WB.8_weibull_failure.png)
![The effects of [math]\displaystyle{ \eta\,\! }[/math] on the Weibull pdf for a common [math]\displaystyle{ \beta\,\! }[/math].](/images/thumb/d/da/WB.8_effects_of_n.png/450px-WB.8_effects_of_n.png)
![The effect of a positive location parameter, [math]\displaystyle{ \gamma\,\! }[/math], on the position of the Weibull pdf.](/images/thumb/8/8b/WB.8_location_parameter.png/450px-WB.8_location_parameter.png)