The Logistic Distribution: Difference between revisions
| Line 68: | Line 68: | ||
====Characteristics of the Logistic Distribution==== | ====Characteristics of the Logistic Distribution==== | ||
:• The logistic distribution has no shape parameter. This means that the logistic <math>pdf</math> has only one shape, the bell shape, and this shape does not change. The shape of the logistic distribution is very similar to that of the normal distribution. | |||
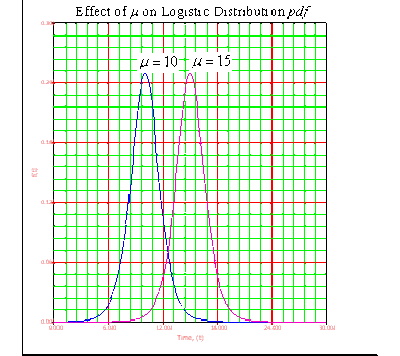
• The logistic distribution has no shape parameter. This means that the logistic <math>pdf</math> has only one shape, the bell shape, and this shape does not change. The shape of the logistic distribution is very similar to that of the normal distribution. | :• The mean, <math>\mu </math> , or the mean life or the <math>MTTF</math> , is also the location parameter of the logistic <math>pdf</math> , as it locates the <math>pdf</math> along the abscissa. It can assume values of <math>-\infty <\bar{T}<\infty </math> . | ||
:• As <math>\mu </math> decreases, the <math>pdf</math> is shifted to the left. | |||
• The mean, <math>\mu </math> , or the mean life or the <math>MTTF</math> , is also the location parameter of the logistic <math>pdf</math> , as it locates the <math>pdf</math> along the abscissa. It can assume values of <math>-\infty <\bar{T}<\infty </math> . | :• As <math>\mu </math> increases, the <math>pdf</math> is shifted to the right. | ||
• As <math>\mu </math> decreases, the <math>pdf</math> is shifted to the left. | |||
• As <math>\mu </math> increases, the <math>pdf</math> is shifted to the right. | |||
[[Image:ldaLD10.2.gif|thumb|center|400px| ]] | [[Image:ldaLD10.2.gif|thumb|center|400px| ]] | ||
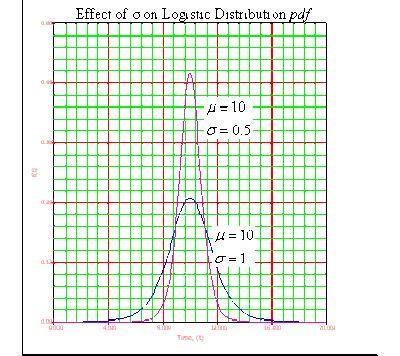
• As <math>\sigma </math> decreases, the <math>pdf</math> gets pushed toward the mean, or it becomes narrower and taller. | :• As <math>\sigma </math> decreases, the <math>pdf</math> gets pushed toward the mean, or it becomes narrower and taller. | ||
:• As <math>\sigma </math> increases, the <math>pdf</math> spreads out away from the mean, or it becomes broader and shallower. | |||
• As <math>\sigma </math> increases, the <math>pdf</math> spreads out away from the mean, or it becomes broader and shallower. | :• The scale parameter can assume values of <math>0<\sigma <\infty </math>. | ||
• The scale parameter can assume values of <math>0<\sigma <\infty </math>. | |||
[[Image:ldaLD10.3.gif|thumb|center|400px| ]] | [[Image:ldaLD10.3.gif|thumb|center|400px| ]] | ||
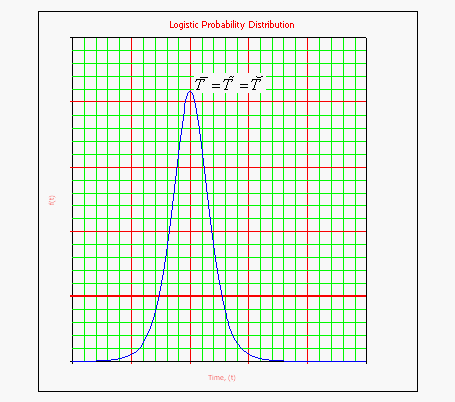
• The logistic <math>pdf</math> starts at <math>T=-\infty </math> with an <math>f(T)=0</math> . As <math>T</math> increases, <math>f(T)</math> also increases, goes through its point of inflection and reaches its maximum value at <math>T=\bar{T}</math> . Thereafter, <math>f(T)</math> decreases, goes through its point of inflection and assumes a value of <math>f(T)=0</math> at <math>T=+\infty </math> . | :• The logistic <math>pdf</math> starts at <math>T=-\infty </math> with an <math>f(T)=0</math> . As <math>T</math> increases, <math>f(T)</math> also increases, goes through its point of inflection and reaches its maximum value at <math>T=\bar{T}</math> . Thereafter, <math>f(T)</math> decreases, goes through its point of inflection and assumes a value of <math>f(T)=0</math> at <math>T=+\infty </math> . | ||
:• For <math>T=\pm \infty ,</math> the <math>pdf</math> equals <math>0.</math> The maximum value of the <math>pdf</math> occurs at <math>T</math> = <math>\mu </math> and equals <math>\tfrac{1}{4\sigma }.</math> | |||
• For <math>T=\pm \infty ,</math> the <math>pdf</math> equals <math>0.</math> The maximum value of the <math>pdf</math> occurs at <math>T</math> = <math>\mu </math> and equals <math>\tfrac{1}{4\sigma }.</math> | :• The point of inflection of the <math>pdf</math> plot is the point where the second derivative of the <math>pdf</math> equals zero. The inflection point occurs at <math>T=\mu +\sigma \ln (2\pm \sqrt{3})</math> or <math>T\approx \mu \pm \sigma 1.31696</math>. | ||
:• If the location parameter <math>\mu </math> decreases, the reliability plot is shifted to the left. If <math>\mu </math> increases, the reliability plot is shifted to the right. | |||
• The point of inflection of the <math>pdf</math> plot is the point where the second derivative of the <math>pdf</math> equals zero. The inflection point occurs at <math>T=\mu +\sigma \ln (2\pm \sqrt{3})</math> or <math>T\approx \mu \pm \sigma 1.31696</math>. | :• If <math>T=\mu </math> then <math>R=0.5</math> . is the inflection point. If <math>T<\mu </math> then <math>R(t)</math> is concave (concave down); if <math>T>\mu </math> then <math>R(t)</math> is convex (concave up). For <math>T<\mu ,</math> <math>\lambda (t)</math> is convex (concave up), for <math>T>\mu ;</math> <math>\lambda (t)</math> is concave (concave down). | ||
:• The main difference between the normal distribution and logistic distribution lies in the tails and in the behavior of the failure rate function. The logistic distribution has slightly longer tails compared to the normal distribution. Also, in the upper tail of the logistic distribution, the failure rate function levels out for large <math>t</math> approaching 1/ <math>\delta .</math> | |||
• If the location parameter <math>\mu </math> decreases, the reliability plot is shifted to the left. If <math>\mu </math> increases, the reliability plot is shifted to the right. | :• If location parameter <math>\mu </math> decreases, the failure rate plot is shifted to the left. Vice versa if <math>\mu </math> increases, the failure rate plot is shifted to the right. | ||
:• <math>\lambda </math> always increases. For <math>T\to -\infty </math> for <math>T\to \infty </math> It is always <math>0\le \lambda (t)\le \tfrac{1}{\sigma }.</math> | |||
• If <math>T=\mu </math> then <math>R=0.5</math> . is the inflection point. If <math>T<\mu </math> then <math>R(t)</math> is concave (concave down); if <math>T>\mu </math> then <math>R(t)</math> is convex (concave up). For <math>T<\mu ,</math> <math>\lambda (t)</math> is convex (concave up), for <math>T>\mu ;</math> <math>\lambda (t)</math> is concave (concave down). | :• If <math>\sigma </math> increases, then <math>\lambda (t)</math> increases more slowly and smoothly. The segment of time where <math>0<\lambda (t)<\tfrac{1}{\sigma }</math> increases, too, whereas the region where <math>\lambda (t)</math> is close to <math>0</math> or <math>\tfrac{1}{\sigma }</math> gets narrower. Conversely, if <math>\sigma </math> decreases, then <math>\lambda (t)</math> increases more quickly and sharply. The segment of time where <math>0<</math> <math>\lambda (t)<\tfrac{1}{\sigma }</math> decreases, too, whereas the region where <math>\lambda (t)</math> is close to <math>0</math> or <math>\tfrac{1}{\sigma }</math> gets broader. | ||
• The main difference between the normal distribution and logistic distribution lies in the tails and in the behavior of the failure rate function. The logistic distribution has slightly longer tails compared to the normal distribution. Also, in the upper tail of the logistic distribution, the failure rate function levels out for large <math>t</math> approaching 1/ <math>\delta .</math> | |||
• If location parameter <math>\mu </math> decreases, the failure rate plot is shifted to the left. Vice versa if <math>\mu </math> increases, the failure rate plot is shifted to the right. | |||
• <math>\lambda </math> always increases. For <math>T\to -\infty </math> for <math>T\to \infty </math> It is always <math>0\le \lambda (t)\le \tfrac{1}{\sigma }.</math> | |||
• If <math>\sigma </math> increases, then <math>\lambda (t)</math> increases more slowly and smoothly. The segment of time where <math>0<\lambda (t)<\tfrac{1}{\sigma }</math> increases, too, whereas the region where <math>\lambda (t)</math> is close to <math>0</math> or <math>\tfrac{1}{\sigma }</math> gets narrower. Conversely, if <math>\sigma </math> decreases, then <math>\lambda (t)</math> increases more quickly and sharply. The segment of time where <math>0<</math> <math>\lambda (t)<\tfrac{1}{\sigma }</math> decreases, too, whereas the region where <math>\lambda (t)</math> is close to <math>0</math> or <math>\tfrac{1}{\sigma }</math> gets broader. | |||
====Weibull++ Notes on Negative Time Values==== | ====Weibull++ Notes on Negative Time Values==== | ||
Revision as of 20:33, 19 August 2011
The Logistic Distribution
The logistic distribution has been used for growth models, and is used in a certain type of regression known as the logistic regression. It has also applications in modeling life data. The shape of the logistic distribution and the normal distribution are very similar [27]. There are some who argue that the logistic distribution is inappropriate for modeling lifetime data because the left-hand limit of the distribution extends to negative infinity. This could conceivably result in modeling negative times-to-failure. However, provided that the distribution in question has a relatively high mean and a relatively small location parameter, the issue of negative failure times should not present itself as a problem.
Logistic Probability Density Function
The logistic
- where:
The Logistic Mean, Median and Mode
The logistic mean or MTTF is actually one of the parameters of the distribution, usually denoted as
The Logistic Standard Deviation
The standard deviation of the logistic distribution,
The Logistic Reliability Function
The reliability for a mission of time
- or:
The unreliability function is:
- where:
The Logistic Conditional Reliability Function
The logistic conditional reliability function is given by:
The Logistic Reliable Life
The logistic reliable life is given by:
The Logistic Failure Rate Function
The logistic failure rate function is given by:
Characteristics of the Logistic Distribution
- • The logistic distribution has no shape parameter. This means that the logistic
- • The mean,
- • As
- • As
- • As
- • As
- • The scale parameter can assume values of
- • The logistic
- • For
- • The point of inflection of the
- • If the location parameter
- • If
- • The main difference between the normal distribution and logistic distribution lies in the tails and in the behavior of the failure rate function. The logistic distribution has slightly longer tails compared to the normal distribution. Also, in the upper tail of the logistic distribution, the failure rate function levels out for large
- • If location parameter
- •
- • If
Weibull++ Notes on Negative Time Values
One of the disadvantages of using the logistic distribution for reliability calculations is the fact that the logistic distribution starts at negative infinity. This can result in negative values for some of the results. Negative values for time are not accepted in most of the components of Weibull++, nor are they implemented. Certain components of the application reserve negative values for suspensions, or will not return negative results. For example, the Quick Calculation Pad will return a null value (zero) if the result is negative. Only the Free-Form (Probit) data sheet can accept negative values for the random variable (x-axis values).
Probability Paper
The form of the Logistic probability paper is based on linearizing the
or using Eqn. (z func of parameters)
Then:
Now let:
and:
which results in the following linear equation:
The logistic probability paper resulting from this linearized
Since the logistic distribution is symmetrical, the area under the
For
Confidence Bounds
In this section, we present the methods used in the application to estimate the different types of confidence bounds for logistically distributed data. The complete derivations were presented in detail (for a general function) in Chapter 5.
Bounds on the Parameters
The lower and upper bounds on the location parameter
The lower and upper bounds on the scale parameter
where
If
The variances and covariances of
Bounds on Reliability
The reliability of the logistic distribution is:
where:
Here
where:
or:
The upper and lower bounds on reliability are:
Bounds on Time
The bounds around time for a given logistic percentile (unreliability) are estimated by first solving the reliability equation with respect to time as follows:
where:
or:
The upper and lower bounds are then found by:
A Logistic Distribution Example
The lifetime of a mechanical valve is known to follow a logistic distribution. Ten units were tested for 28 months and the following months-to-failure data was collected.
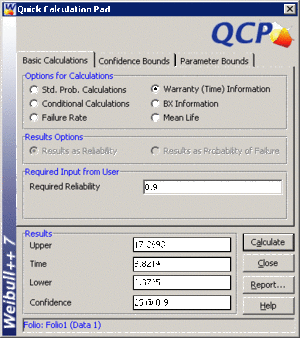
• Determine the valve's design life if specifications call for a reliability goal of 0.90.
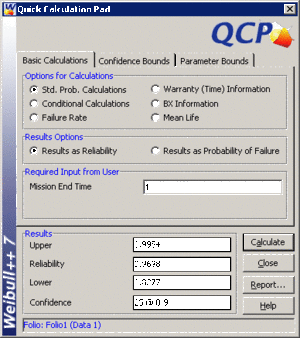
• The valve is to be used in a pumping device that requires 1 month of continuous operation. What is the probability of the pump failing due to the valve?
This data set can be entered into Weibull++ as follows:
The computed parameters for maximum likelihood are:
• The valve's design life, along with 90% two sided confidence bounds, can be obtained using the QCP as follows:
• The probability, along with 90% two sided confidence bounds, that the pump fails due to a valve failure during the first month is obtained as follows: