The Weibull Distribution: Difference between revisions
| Line 319: | Line 319: | ||
<br>for <math>MR</math>, where <math>N</math> is the sample size and <math>i</math> the order number. The times-to-failure, with their corresponding median ranks, are shown next. | <br>for <math>MR</math>, where <math>N</math> is the sample size and <math>i</math> the order number. The times-to-failure, with their corresponding median ranks, are shown next. | ||
{| border="1" cellspacing="1" | {|align="center" border="1" cellspacing="1" | ||
|- | |- | ||
| Time-to-failure, hrs | | Time-to-failure, hrs | ||
Revision as of 22:43, 21 July 2011
The Weibull Distribution
The Weibull distribution is one of the most widely used lifetime distributions in reliability engineering. It is a versatile distribution that can take on the characteristics of other types of distributions, based on the value of the shape parameter, [math]\displaystyle{ \boldsymbol{\beta} }[/math]. This chapter provides a brief background on the Weibull distribution, presents and derives most of the applicable equations and presents examples calculated both manually and by using ReliaSoft's Weibull++.
Weibull Probability Density Function
The Three-Parameter Weibull Distribution
The three-parameter Weibull pdf is given by:
- [math]\displaystyle{ f(T)={ \frac{\beta }{\eta }}\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta -1}e^{-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }} }[/math]
where,
- [math]\displaystyle{ f(T)\geq 0,\text{ }T\geq 0\text{ or }\gamma, }[/math]
- [math]\displaystyle{ \beta\gt 0\ \,\! }[/math],
- [math]\displaystyle{ \eta \gt 0 \,\! }[/math],
- [math]\displaystyle{ -\infty \lt \gamma \lt +\infty \,\! }[/math]
and,
- [math]\displaystyle{ \eta= \,\! }[/math] scale parameter, or characteristic life
- [math]\displaystyle{ \beta= \,\! }[/math] shape parameter (or slope),
- [math]\displaystyle{ \gamma= \,\! }[/math] location parameter (or failure free life).
The Two-Parameter Weibull Distribution
The two-parameter Weibull pdf is obtained by setting [math]\displaystyle{ \gamma=0 \,\! }[/math], and is given by:
- [math]\displaystyle{ f(T)={ \frac{\beta }{\eta }}\left( {\frac{T}{\eta }}\right) ^{\beta -1}e^{-\left( { \frac{T}{\eta }}\right) ^{\beta }} \,\! }[/math]
The One-Parameter Weibull Distribution
The one-parameter Weibull pdf is obtained by again setting [math]\displaystyle{ \gamma=0 \,\! }[/math] and assuming [math]\displaystyle{ \beta=C=Constant \,\! }[/math] assumed value or:
- [math]\displaystyle{ f(T)={ \frac{C}{\eta }}\left( {\frac{T}{\eta }}\right) ^{C-1}e^{-\left( {\frac{T}{ \eta }}\right) ^{C}} \,\! }[/math]
where the only unknown parameter is the scale parameter, [math]\displaystyle{ \eta\,\! }[/math].
Note that in the formulation of the one-parameter Weibull, we assume that the shape parameter [math]\displaystyle{ \beta \,\! }[/math] is known a priori from past experience on identical or similar products. The advantage of doing this is that data sets with few or no failures can be analyzed.
Weibull Statistical Properties
The Mean or MTTF
The mean, [math]\displaystyle{ \overline{T} \,\! }[/math], (also called MTTF of the Weibull pdf is given by:
- [math]\displaystyle{ \overline{T}=\gamma +\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
where
- [math]\displaystyle{ \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
is the gamma function evaluated at the value of
- [math]\displaystyle{ \left( { \frac{1}{\beta }}+1\right) \,\! }[/math].
The gamma function is defined as:
- [math]\displaystyle{ \Gamma (n)=\int_{0}^{\infty }e^{-x}x^{n-1}dx \,\! }[/math]
For the two-parameter case, this can be reduced to:
- [math]\displaystyle{ \overline{T}=\eta \cdot \Gamma \left( {\frac{1}{\beta }}+1\right) \,\! }[/math]
Note that some practitioners erroneously assume that [math]\displaystyle{ \eta \,\! }[/math] is equal to the MTTF, [math]\displaystyle{ \overline{T}\,\! }[/math]. This is only true for the case of [math]\displaystyle{ \beta=1 \,\! }[/math] or
- [math]\displaystyle{ \begin{align} \overline{T} &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\ &= \eta \cdot \Gamma \left( {\frac{1}{1}}+1\right) \\ &= \eta \cdot \Gamma \left( {2}\right) \\ &= \eta \cdot 1\\ &= \eta \end{align} }[/math]
The Median
The median, [math]\displaystyle{ \breve{T}, }[/math] of the Weibull distribution is given by:
- [math]\displaystyle{ \breve{T}=\gamma +\eta \left( \ln 2\right) ^{\frac{1}{\beta }} }[/math]
The Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] is given by:
- [math]\displaystyle{ \tilde{T}=\gamma +\eta \left( 1-\frac{1}{\beta }\right) ^{\frac{1}{\beta }} }[/math]
The Standard Deviation
The standard deviation, σT, is given by:
- [math]\displaystyle{ \sigma _{T}=\eta \cdot \sqrt{\Gamma \left( {\frac{2}{\beta }}+1\right) -\Gamma \left( {\frac{1}{ \beta }}+1\right) ^{2}} }[/math]
The Weibull Reliability Function
The equation for the three-parameter Weibull cumulative density function, cdf, is given by:
- [math]\displaystyle{ F(T)=1-e^{-\left( \frac{T-\gamma }{\eta }\right) ^{\beta }} }[/math].
This is also referred to as Unreliability and deignated as [math]\displaystyle{ Q(T) \,\! }[/math] by some authors.
Recalling that the reliability function of a distribution is simply one minus the cdf, the reliability function for the three-parameter Weibull distribution is then given by:
- [math]\displaystyle{ R(T)=e^{-\left( { \frac{T-\gamma }{\eta }}\right) ^{\beta }} }[/math]
The Weibull Conditional Reliability Function
The three-parameter Weibull conditional reliability function is given by:
- [math]\displaystyle{ R(t|T)={ \frac{R(T+t)}{R(T)}}={\frac{e^{-\left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }}}{e^{-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }}}} }[/math]
or:
- [math]\displaystyle{ R(t|T)=e^{-\left[ \left( {\frac{T+t-\gamma }{\eta }}\right) ^{\beta }-\left( {\frac{T-\gamma }{\eta }}\right) ^{\beta }\right] } }[/math]
These gives the reliability for a new mission of [math]\displaystyle{ t \,\! }[/math] duration, having already accumulated [math]\displaystyle{ T \,\! }[/math] time of operation up to the start of this new mission, and the units are checked out to assure that they will start the next mission successfully. It is called conditional because you can calculate the reliability of a new mission based on the fact that the unit or units already accumulated hours of operation successfully.
The Weibull Reliable Life
The reliable life, [math]\displaystyle{ T_{R} \,\! }[/math], of a unit for a specified reliability,[math]\displaystyle{ R \,\! }[/math], starting the mission at age zero, is given by:
- [math]\displaystyle{ T_{R}=\gamma +\eta \cdot \left\{ -\ln ( R ) \right\} ^{ \frac{1}{\beta }} }[/math]
This is the life for which the unit/item will be functioning successfully with a reliability of [math]\displaystyle{ R \,\! }[/math], . If ,[math]\displaystyle{ R=0.50 \,\! }[/math], then [math]\displaystyle{ T_{R}=\breve{T} }[/math], the median life, or the life by which half of the units will survive.
The Weibull Failure Rate Function
The Weibull failure rate function, [math]\displaystyle{ \lambda(t) \,\! }[/math], is given by:
- [math]\displaystyle{ \lambda \left( T\right) = \frac{f\left( T\right) }{R\left( T\right) }=\frac{\beta }{\eta }\left( \frac{ T-\gamma }{\eta }\right) ^{\beta -1} }[/math]
Characteristics of the Weibull Distribution
As was mentioned previously, the Weibull distribution is widely used in reliability and life data analysis due to its versatility. Depending on the values of the parameters, the Weibull distribution can be used to model a variety of life behaviors. We will now examine how the values of the shape parameter, β, and the scale parameter, η, affect such distribution characteristics as the shape of the curve, the reliability and the failure rate. Note that in the rest of this section we will assume the most general form of the Weibull distribution, i.e. the three-parameter form. The appropriate substitutions to obtain the other forms, such as the two-parameter form where γ = 0, or the one-parameter form where β = C = constant, can easily be made.
Characteristic Effects of the Shape Parameter, β
The Weibull shape parameter, β, is also known as the slope. This is because the value of β is equal to the slope of the regressed line in a probability plot. Different values of the shape parameter can have marked effects on the behavior of the distribution. In fact, some values of the shape parameter will cause the distribution equations to reduce to those of other distributions. For example, when β = 1, the of the three-parameter Weibull reduces to that of the two-parameter exponential distribution or:
- [math]\displaystyle{ f(T)={\frac{1}{\eta }}e^{-{\frac{T-\gamma }{\eta }}} }[/math]
where [math]\displaystyle{ \frac{1}{\eta }=\lambda = }[/math] failure rate. The parameter β is a pure number, i.e. it is dimensionless.
The Effect of β on the [math]\displaystyle{ pdf }[/math]
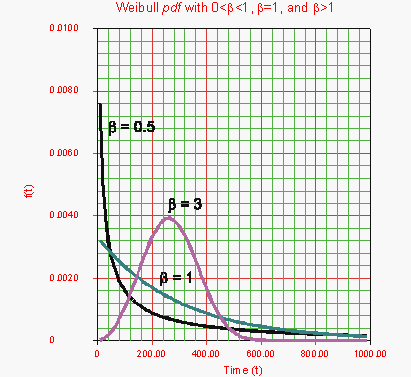
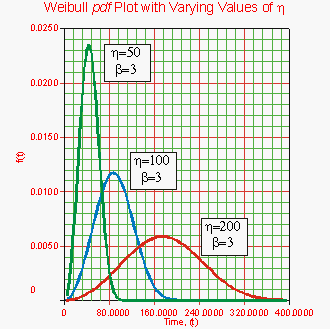
Figure 6-1 shows the effect of different values of the shape parameter, β, on the shape of the [math]\displaystyle{ pdf }[/math]. One can see that the shape of the can take on a variety of forms based on the value of β.
- Figure 6.1: The effect of the Weibull shape parameter on the [math]\displaystyle{ pdf }[/math].
For [math]\displaystyle{ 0\lt \beta \leq 1 }[/math]:
- As T→0 (or γ), f(T)→∞.
- As T→∞, f(T)→0.
- f(T) decreases monotonically and is convex as increases beyond the value of γ.
- The mode is non-existent.
For β > 1:
- f(T) = 0 at (or γ).
- f(T) increases as [math]\displaystyle{ T\rightarrow \tilde{T} }[/math] (the mode) and decreases thereafter.
- For β < 2.6 the Weibull [math]\displaystyle{ pdf }[/math] is positively skewed (has a right tail), for 2.6 < β < 3.7 its coefficient of skewness approaches zero (no tail). Consequently, it may approximate the normal [math]\displaystyle{ pdf }[/math] , and for β > 3.7 it is negatively skewed (left tail). The way the value of β relates to the physical behavior of the items being modeled becomes more apparent when we observe how its different values affect the reliability and failure rate functions. Note that for β = 0.999, f(0) = ∞, but for β = 1.001, f(0) = 0. This abrupt shift is what complicates MLE estimation when β is close to one.
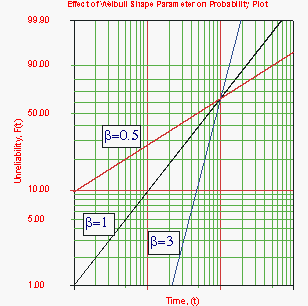
The Effect of β on the [math]\displaystyle{ cdf }[/math] and Reliability Function
- Figure 6.2: Effect on [math]\displaystyle{ \beta }[/math] on the [math]\displaystyle{ cdf }[/math] on the Weibull probability plot with a fixed value of [math]\displaystyle{ \eta }[/math].
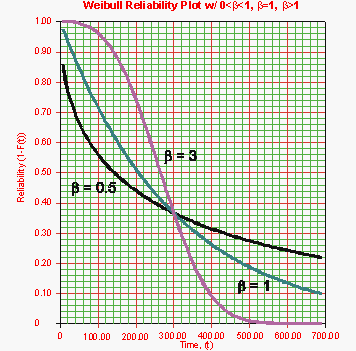
Figure 6-2 shows the effect of the value of β on the [math]\displaystyle{ cdf }[/math], as manifested in the Weibull probability plot. It is easy to see why this parameter is sometimes referred to as the slope. Note that the models represented by the three lines all have the same value of η. Figure 6-3 shows the effects of these varied values of β on the reliability plot, which is a linear analog of the probability plot.
- Figure 6.3: The effect of values of [math]\displaystyle{ \beta }[/math] on the Weibull reliability plot.
- R(T) decreases sharply and monotonically for 0 < β < 1 and is convex.
- For β = 1, R(T) decreases monotonically but less sharply than for 0 < β < 1 and is convex.
- For β > 1, R(T) decreases as increases. As wear-out sets in, the curve goes through an inflection point and decreases sharply.
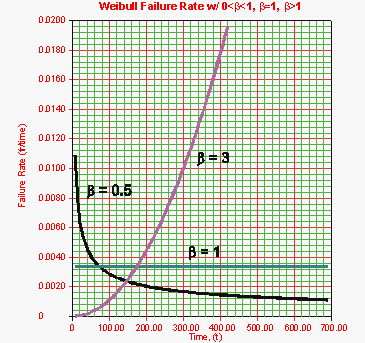
The Effect of β on the Weibull Failure Rate
The value of β has a marked effect on the failure rate of the Weibull distribution and inferences can be drawn about a population's failure characteristics just by considering whether the value of β is less than, equal to, or greater than one.
- Figure 6.4: The effect of [math]\displaystyle{ \beta }[/math] on the Weibull failure rate function.
As indicated by Figure 6-4, populations with β < 1 exhibit a failure rate that decreases with time, populations with β = 1 have a constant failure rate (consistent with the exponential distribution) and populations with β > 1 have a failure rate that increases with time. All three life stages of the bathtub curve can be modeled with the Weibull distribution and varying values of β. The Weibull failure rate for 0 < β < 1 is unbounded at (or γ). The failure rate, λ(T), decreases thereafter monotonically and is convex, approaching the value of zero as T→∞ or λ(∞) = 0. This behavior makes it suitable for representing the failure rate of units exhibiting early-type failures, for which the failure rate decreases with age. When encountering such behavior in a manufactured product, it may be indicative of problems in the production process, inadequate burn-in, substandard parts and components, or problems with packaging and shipping. For β = 1, λ(T) yields a constant value of [math]\displaystyle{ { \frac{1}{\eta }} }[/math] or:
- [math]\displaystyle{ \lambda (T)=\lambda ={\frac{1}{\eta }} }[/math]
This makes it suitable for representing the failure rate of chance-type failures and the useful life period failure rate of units.
For β > 1, λ(T) increases as increases and becomes suitable for representing the failure rate of units exhibiting wear-out type failures. For 1 < β < 2, the λ(T) curve is concave, consequently the failure rate increases at a decreasing rate as increases.
For β = 2 there emerges a straight line relationship between λ(T) and , starting at a value of λ(T) = 0 at T = γ, and increasing thereafter with a slope of [math]\displaystyle{ { \frac{2}{\eta ^{2}}} }[/math]. Consequently, the failure rate increases at a constant rate as increases. Furthermore, if η = 1 the slope becomes equal to 2, and when γ = 0, λ(T) becomes a straight line which passes through the origin with a slope of 2. Note that at β = 2, the Weibull distribution equations reduce to that of the Rayleigh distribution.
When β > 2, the λ(T) curve is convex, with its slope increasing as increases. Consequently, the failure rate increases at an increasing rate as increases indicating wear-out life.
Characteristic Effects of the Scale Parameter, η
- Figure 6.5: The effects of [math]\displaystyle{ \eta }[/math] on the Weibull [math]\displaystyle{ pdf }[/math] for a common [math]\displaystyle{ \beta }[/math].
A change in the scale parameter η has the same effect on the distribution as a change of the abscissa scale. Increasing the value of η while holding β constant has the effect of stretching out the . Since the area under a curve is a constant value of one, the "peak" of the pdf curve will also decrease with the increase of η, as indicated in Figure 6-5.
- If η is increased while β and γ are kept the same, the distribution gets stretched out to the right and its height decreases, while maintaining its shape and location.
- If η is decreased while β and γ are kept the same, the distribution gets pushed in towards the left (i.e. towards its beginning or towards 0 or γ), and its height increases.
- η has the same units as , such as hours, miles, cycles, actuations, etc.
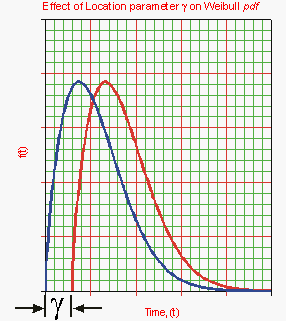
Characteristic Effects of the Location Parameter, γ
The location parameter, γ, as the name implies, locates the distribution along the abscissa. Changing the value of γ has the effect of sliding the distribution and its associated function either to the right (if γ > 0) or to the left (if γ < 0).
- Figure 6.6: The effect of a positive location parameter, [math]\displaystyle{ \gamma }[/math], on the position of the Weibull [math]\displaystyle{ pdf }[/math].
- When γ = 0, the distribution starts at or at the origin.
- If γ > 0, the distribution starts at the location γ to the right of the origin.
- If γ < 0, the distribution starts at the location γ to the left of the origin.
- γ provides an estimate of the earliest time-to-failure of such units.
- The life period 0 to + γ is a failure free operating period of such units.
- The parameter γ may assume all values and provides an estimate of the earliest time a failure may be observed. A negative γ may indicate that failures have occurred prior to the beginning of the test, namely during production, in storage, in transit, during checkout prior to the start of a mission, or prior to actual use.
- γ has the same units as T, such as hours, miles, cycles, actuations, etc.
Estimation of the Weibull Parameters
The estimates of the parameters of the Weibull distribution can be found graphically via probability plotting paper, or analytically, either using least squares or maximum likelihood.
Probability Plotting
One method of calculating the parameters of the Weibull distribution is by using probability plotting. To better illustrate this procedure, consider the following example from Kececioglu [20].
Example
Assume that six identical units are being reliability tested at the same application and operation stress levels. All of these units fail during the test after operating the following number of hours, Ti: 93, 34, 16, 120, 53 and 75. Estimate the values of the parameters for a two-parameter Weibull distribution and determine the reliability of the units at a time of 15 hours.
Solution to Example
The steps for determining the parameters of the Weibull representing the data, using probability plotting, are outlined in the following instructions. First, rank the times-to-failure in ascending order as shown next.
| Time-to-failure, hrs |
Failure Order Number out of Sample Size of 6 |
|---|---|
| 16 | 1 |
| 34 | 2 |
| 53 | 3 |
| 75 | 4 |
| 93 | 5 |
| 120 | 6 |
Obtain their median rank plotting positions. Median rank positions are used instead of other ranking methods because median ranks are at a specific confidence level (50%). Median ranks can be found tabulated in many reliability books. They can also be estimated using the following equation,
- [math]\displaystyle{ MR \sim { \frac{i-0.3}{N+0.4}}\cdot 100, }[/math]
where [math]\displaystyle{ i }[/math] is the failure order number and [math]\displaystyle{ N }[/math] is the total sample size. The exact median ranks are found in Weibull++ by solving,
- [math]\displaystyle{ \sum_{k=i}^N{\binom{N}{k}}{MR^k}{(1-MR)^{N-k}}=0.5=50% }[/math]
for [math]\displaystyle{ MR }[/math], where [math]\displaystyle{ N }[/math] is the sample size and [math]\displaystyle{ i }[/math] the order number. The times-to-failure, with their corresponding median ranks, are shown next.
| Time-to-failure, hrs | Median Rank,% |
| 16 | 10.91 |
| 34 | 26.44 |
| 53 | 42.14 |
| 75 | 57.86 |
| 93 | 73.56 |
| 120 | 89.1 |
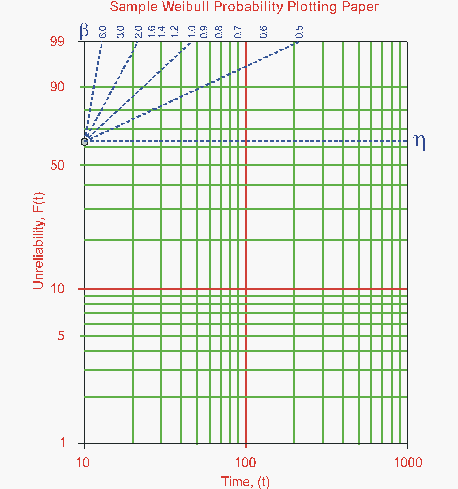
On a Weibull probability paper, plot the times and their corresponding ranks. A sample of a Weibull probability paper is given in Figure 6-7 and the plot of the data in the example in Figure 6-8.
- Figure 6.7: Example of Weibull probability plotting paper.
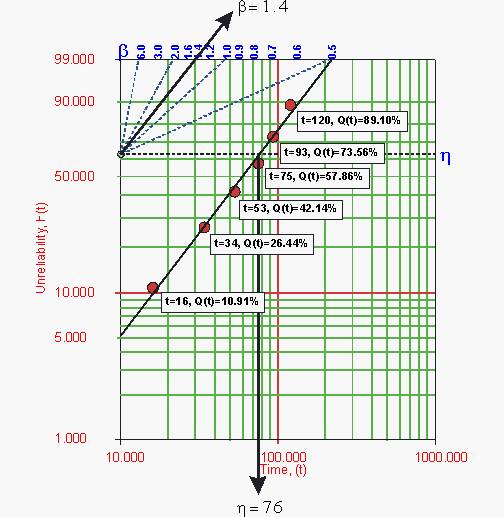
Draw the best possible straight line through these points, as shown below, then obtain the slope of this line by drawing a line, parallel to the one just obtained, through the slope indicator. This value is the estimate of the shape parameter [math]\displaystyle{ \hat{\beta } }[/math], in this case [math]\displaystyle{ \hat{\beta }=1.4 }[/math].
- Figure 6.8: Probability plot of data in Example 1.
At the [math]\displaystyle{ Q(t)=63.2% }[/math] ordinate point, draw a straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of [math]\displaystyle{ \hat{\eta } }[/math]. For this case, [math]\displaystyle{ \hat{\eta }=76 }[/math] hours. (This is always at 63.2% since: [math]\displaystyle{ Q(T)=1-e^{-(\frac{\eta }{\eta })^{\beta }}=1-e^{-1}=0.632=63.2% }[/math].
Now any reliability value for any mission time [math]\displaystyle{ t }[/math] can be obtained. For example, the reliability for a mission of 15 hours, or any other time, can now be obtained either from the plot or analytically. To obtain the value from the plot, draw a vertical line from the abscissa, at hours, to the fitted line. Draw a horizontal line from this intersection to the ordinate and read Q(t), in this case [math]\displaystyle{ Q(t)=9.8% }[/math]. Thus, [math]\displaystyle{ R(t)=1-Q(t)=90.2% }[/math]. This can also be obtained analytically from the Weibull reliability function since the estimates of both of the parameters are known or:
[math]\displaystyle{ R(t=15)=e^{-\left( \frac{15}{\eta }\right) ^{\beta }}=e^{-\left( \frac{15}{76 }\right) ^{1.4}}=90.2% }[/math]
Probability Plotting for the Location Parameter, γ
The third parameter of the Weibull distribution is utilized when the data do not fall on a straight line, but fall on either a concave up or down curve. The following statements can be made regarding the value of γ:
Case 1: If the curve for MR versus Tj is concave down and the curve for MR versus (Tj − T1) is concave up, then there exists a γ such that 0 < γ < T1, or γ has a positive value.
Case 2: If the curves for MR versus Tj and MR versus (Tj − T1) are both concave up, then there exists a negative γ which will straighten out the curve of MR versus Tj.
Case 3: If neither one of the previous two cases prevails, then either reject the Weibull as one capable of representing the data, or proceed with the multiple population (mixed Weibull) analysis. To obtain the location parameter, γ:
- Subtract the same arbitrary value, γ, from all the times to failure and replot the data.
- If the initial curve is concave up, subtract a negative γ from each failure time.
- If the initial curve is concave down, subtract a positive γ from each failure time.
- Repeat until the data plots on an acceptable straight line.
- The value of γ is the subtracted (positive or negative) value that places the points in an acceptable straight line.
The other two parameters are then obtained using the techniques previously described. Also, it is important to note that we used the term subtract a positive or negative gamma, where subtracting a negative gamma is equivalent to adding it. Note that when adjusting for gamma, the x-axis scale for the straight line becomes (T − γ).
SUBSUBSECTION
Example 2
Six identical units are reliability tested under the same stresses and conditions. All units are tested to failure and the following times-to-failure are recorded: 48, 66, 85, 107, 125 and 152 hours. Find the parameters of the three-parameter Weibull distribution using probability plotting.
Solution to Example 2
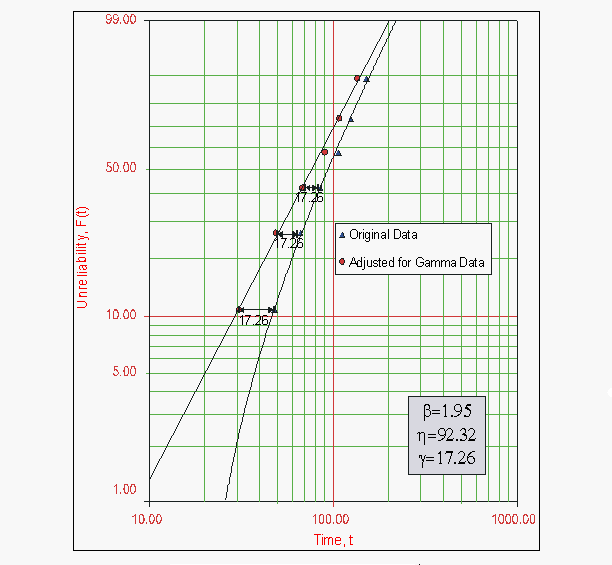
The following figure shows the results. Note that since the original data set was concave down, 17.26 was subtracted from all the times-to-failure and replotted, resulting in a straight line, thus γ = 17.26. (We used Weibull++ to get the results. To perform this by hand, one would attempt different values of γ, using a trial and error methodology, until an acceptable straight line is found. When performed manually, you do not expect decimal accuracy.)
- Figure 6.9: Probability Plot of data in Example 2.
Rank Regression on Y
Performing rank regression on Y requires that a straight line mathematically be fitted to a set of data points such that the sum of the squares of the vertical deviations from the points to the line is minimized. This is in essence the same methodology as the probability plotting method, except that we use the principle of least squares to determine the line through the points, as opposed to just eyeballing it. The first step is to bring our function into a linear form. For the two-parameter Weibull distribution, the (cumulative density function) is:
- [math]\displaystyle{ F(T)=1-e^{-\left( \frac{T}{\eta }\right) ^{\beta }} (Fw) }[/math]
Taking the natural logarithm of both sides of the equation yields:
- [math]\displaystyle{ \ln[ 1-F(T)] =-( \frac{T}{\eta }) ^{\beta } }[/math]
- [math]\displaystyle{ \ln{ -\ln[ 1-F(T)]} =\beta \ln ( \frac{T}{ \eta }) }[/math]
or:
- [math]\displaystyle{ \ln \{ -\ln[ 1-F(T)]\} =-\beta \ln (\eta )+\beta \ln (T) EQNREF logw }[/math]
Now let:
- [math]\displaystyle{ y = \ln \{ -\ln[ 1-F(T)]\} ( yw ) }[/math]
- [math]\displaystyle{ a = − βln(\eta) }[/math] (aw)
and:
- [math]\displaystyle{ b= \beta }[/math] ( bw )
which results in the linear equation of:
- [math]\displaystyle{ y=a+bx }[/math]
The least squares parameter estimation method (also known as regression analysis) was discussed in Chapter 3 and the following equations for regression on Y were derived in Appendix A:
- [math]\displaystyle{ \hat{a}=\frac{\sum\limits_{i=1}^{N}y_{i}}{N}-\hat{b}\frac{ \sum\limits_{i=1}^{N}x_{i}}{N}=\bar{y}-\hat{b}\bar{x} EQNREF aaw }[/math]
and:
- [math]\displaystyle{ \hat{b}={\frac{\sum\limits_{i=1}^{N}x_{i}y_{i}-\frac{\sum \limits_{i=1}^{N}x_{i}\sum\limits_{i=1}^{N}y_{i}}{N}}{\sum \limits_{i=1}^{N}x_{i}^{2}-\frac{\left( \sum\limits_{i=1}^{N}x_{i}\right) ^{2}}{N}}} EQNREF bbw }[/math]
In this case the equations for yi and xi are:
- [math]\displaystyle{ y_{i}=\ln \left\{ -\ln [1-F(T_{i})]\right\} , }[/math]
and:
- xi = ln(Ti).
The [math]\displaystyle{ F(T_{i})^{\prime }s }[/math] are estimated from the median ranks.
Once [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math] are obtained, then [math]\displaystyle{ \hat{\beta } }[/math] and [math]\displaystyle{ \hat{\eta } }[/math] can easily be obtained from Eqns. (EQNREF aw ) and (\ref {bw}).
The Correlation Coefficient
The correlation coefficient is defined as follows:
- [math]\displaystyle{ \rho ={\frac{\sigma _{xy}}{\sigma _{x}\sigma _{y}}} }[/math]
where, σx y = covariance of and , σx = standard deviation of , and σy = standard deviation of . The estimator of ρ is the sample correlation coefficient, [math]\displaystyle{ \hat{\rho} }[/math], given by:
- [math]\displaystyle{ \hat{\rho}=\frac{\sum\limits_{i=1}^{N}(x_{i}-\overline{x})(y_{i}-\overline{y} )}{\sqrt{\sum\limits_{i=1}^{N}(x_{i}-\overline{x})^{2}\cdot \sum\limits_{i=1}^{N}(y_{i}-\overline{y})^{2}}} EQNREF RHOw }[/math]
Example 3
Consider the data in Example 1, where six units were tested to failure and the following failure times were recorded: 16, 34, 53, 75, 93 and 120 hours. Estimate the parameters and the correlation coefficient using rank regression on Y, assuming that the data follow the two-parameter Weibull distribution.
Solution to Example 3
Construct a table as shown below.
| N | [math]\displaystyle{ T_{i} }[/math] | [math]\displaystyle{ ln(T_{i}) }[/math] | [math]\displaystyle{ F(T_i) }[/math] | [math]\displaystyle{ y_{i} }[/math] | [math]\displaystyle{ (ln{T_i})^2 }[/math] | [math]\displaystyle{ {y_i}^2 }[/math] | [math]\displaystyle{ (ln{T_i})y_i }[/math] |
| 1 | 16 | 2.7726 | 0.1091 | -2.1583 | 7.6873 | 4.6582 | -5.9840 |
| 2 | 34 | 3.5264 | 0.2645 | -1.1802 | 12.4352 | 1.393 | -4.1620 |
| 3 | 53 | 3.9703 | 0.4214 | -0.6030 | 15.7632 | 0.3637 | -2.3943 |
| 4 | 75 | 4.3175 | 0.5786 | -0.146 | 18.6407 | 0.0213 | -0.6303 |
| 5 | 93 | 4.5326 | 0.7355 | 0.2851 | 20.5445 | 0.0813 | 1.2923 |
| 6 | 120 | 4.7875 | 0.8909 | 0.7955 | 22.9201 | 0.6328 | 3.8083 |
| [math]\displaystyle{ \sum }[/math] | 23.9068 | -3.007 | 97.9909 | 7.1502 | -8.0699 |
Utilizing the values from Table 6.1, calculate [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math] using Eqns. (EQNREF aaw ) and (EQNREF bbw );
[math]\displaystyle{ \hat{b} =\frac{\sum\limits_{i=1}^{6}(\ln T_{i})y_{i}-(\sum\limits_{i=1}^{6}\ln T_{i})(\sum\limits_{i=1}^{6}y_{i})/6}{ \sum\limits_{i=1}^{6}(\ln T_{i})^{2}-(\sum\limits_{i=1}^{6}\ln T_{i})^{2}/6}
}[/math]
- [math]\displaystyle{ \hat{b}=\frac{-8.0699-(23.9068)(-3.0070)/6}{97.9909-(23.9068)^{2}/6} }[/math]
or
- [math]\displaystyle{ \hat{b}=1.4301 }[/math]
and:
- [math]\displaystyle{ \hat{a}=\overline{y}-\hat{b}\overline{T}=\frac{\sum \limits_{i=1}^{N}y_{i}}{N}-\hat{b}\frac{\sum\limits_{i=1}^{N}\ln T_{i}}{N } }[/math]
or:
- [math]\displaystyle{ \hat{a}=\frac{(-3.0070)}{6}-(1.4301)\frac{23.9068}{6}=-6.19935 }[/math]
Therefore, from Eqn. (EQNREF bw ):
- [math]\displaystyle{ \hat{\beta }=\hat{b}=1.4301 }[/math]
and from Eqn. (EQNREF aw ):
- [math]\displaystyle{ \hat{\eta }=e^{-\frac{\hat{a}}{\hat{b}}}=e^{-\frac{(-6.19935)}{ 1.4301}} }[/math]
or:
- [math]\displaystyle{ \hat{\eta }=76.318\text{ hr} }[/math]
The correlation coefficient can be estimated using Eqn. (EQNREF RHOw ):
- [math]\displaystyle{ \hat{\rho }=0.9956 }[/math]
The above example can be repeated using Weibull++. Start Weibull++ and create a new Data Folio.
Select the Times-to-failure data option.
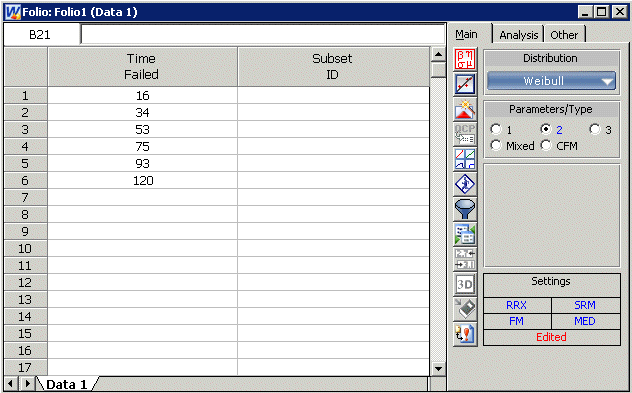
Enter the times-to-failure in the datasheet (ignore the Subset ID column), as shown next. The times-to-failure need not be sorted, Weibull++ will automatically sort the data.
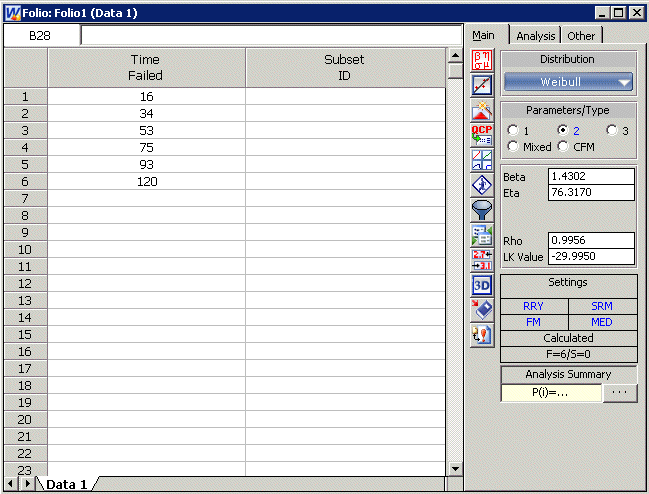
Select the desired method of analysis. Note that we are assuming that the underlying distribution is the Weibull, so make sure that the Weibull distribution is selected. Under Parameters/Type on the Main page, select 2.
Also, so that you get the same results as this example, switch to the Analysis page and make sure you are using the Rank Regression on Y (RRY) calculation method with this example, as shown next.
Note that this can also be done from the Main page by clicking the left bottom box under the Results area. Each time you click that box you will see the method switch between MLE, RRX, and RRY. Click the Calculate icon,
or select Calculate from the Data menu. The results will appear in the Data Folio's Results area. The next figure shows the results for this example.
You can now plot the results by clicking the Plot icon,
or by selecting Plot Probability from the Data menu.
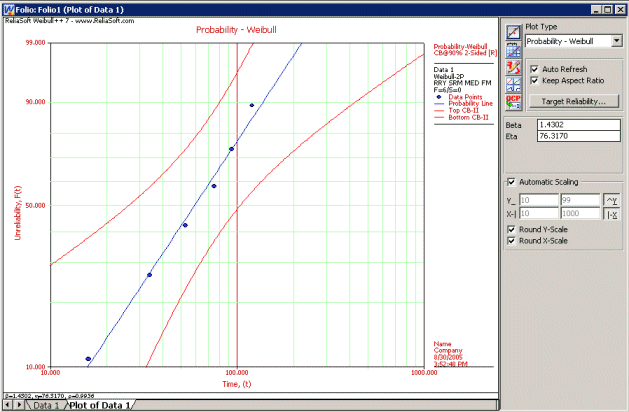
The Weibull probability plot for these data is shown next.
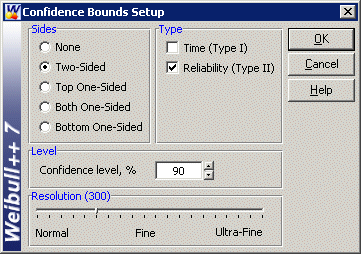
The confidence bounds, as determined from the Fisher matrix, can also be plotted. Select Confidence Bounds from the Plot menu, choose Two-Sided under Sides, Reliability (Type II) under Type and enter 90 for the Confidence level.
The plot will appear as follows,
If desired, the Weibull [math]\displaystyle{ pdf }[/math] representing these data can be written as:
- [math]\displaystyle{ f(T)={\frac{\beta }{\eta }}\left( {\frac{T}{\eta }}\right) ^{\beta -1}e^{-\left( {\frac{T}{\eta }}\right) ^{\beta }} }[/math]
or:
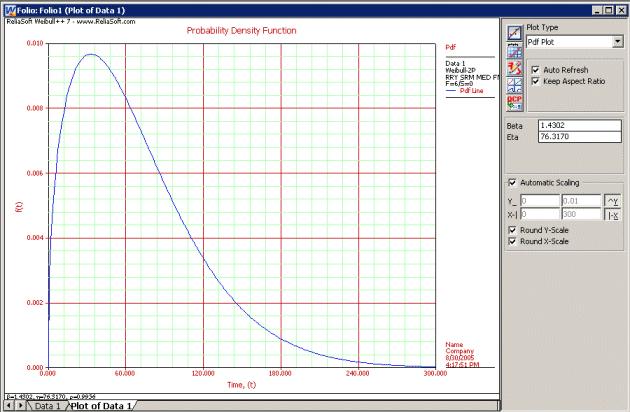
- [math]\displaystyle{ f(T)={\frac{1.4302}{76.317}}\left( {\frac{T}{76.317}}\right) ^{0.4302}e^{-\left( {\frac{T}{76.317}}\right) ^{1.4302}} }[/math] You can also plot the Weibull by selecting Pdf Plot from the Plot Type drop-down menu on the control panel to the right of the plot area.
From this point on, different results, reports and plots can be obtained.
Rank Regression on X
Performing a rank regression on X is similar to the process for rank regression on Y, with the difference being that the horizontal deviations from the points to the line are minimized rather than the vertical. Again, the first task is to bring our function, Eqn. (EQNREF Fw ), into a linear form. This step is exactly the same as in the regression on Y analysis and Eqns. (EQNREF logw ), (EQNREF yw ), (EQNREF aw ) and (EQNREF bw ) apply in this case too. The derivation from the previous analysis begins on the least squares fit part, where in this case we treat as the dependent variable and as the independent variable. The best-fitting straight line to the data, for regression on X (see Chapter 3), is the straight line:
- [math]\displaystyle{ x= \hat{a}+\hat{b}y }[/math] EQNREF xlinew
The corresponding equations for [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math] are:
- [math]\displaystyle{ \hat{a}=\overline{x}-\hat{b}\overline{y}=\frac{\sum\limits_{i=1}^{N}x_{i}}{N} -\hat{b}\frac{\sum\limits_{i=1}^{N}y_{i}}{N} }[/math]
and
- [math]\displaystyle{ \hat{b}={\frac{\sum\limits_{i=1}^{N}x_{i}y_{i}-\frac{\sum \limits_{i=1}^{N}x_{i}\sum\limits_{i=1}^{N}y_{i}}{N}}{\sum \limits_{i=1}^{N}y_{i}^{2}-\frac{\left( \sum\limits_{i=1}^{N}y_{i}\right) ^{2}}{N}}} }[/math]
where:
- [math]\displaystyle{ y_{i}=\ln \left\{ -\ln [1-F(T_{i})]\right\} }[/math] and:
xi = ln(Ti) and the F(Ti) values are again obtained from the median ranks.
Once [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math] are obtained, solve Eqn. (EQNREF xlinew ) for y, which corresponds to:
- [math]\displaystyle{ y=-\frac{\hat{a}}{\hat{b}}+\frac{1}{\hat{b}}x }[/math] Solving for the parameters from Eqns. (EQNREF aw ) and (EQNREF bw ) we get
- [math]\displaystyle{ a=-\frac{\hat{a}}{\hat{b}}=-\beta \ln (\eta ) }[/math] EQNREF awx
and
- [math]\displaystyle{ b=\frac{1}{\hat{b}}=\beta EQNREF bwx }[/math] The correlation coefficient is evaluated as before using Eqn. (EQNREF RHOw ).
Example 4
Repeat Example 1 using rank regression on X.
Solution to Example 4
Solution to Example 4 Table 6.1, constructed in Example 3, can also be applied to this example.
Using the values from this table we get:
- [math]\displaystyle{ \hat{b} ={\frac{\sum\limits_{i=1}^{6}(\ln T_{i})y_{i}-\frac{ \sum\limits_{i=1}^{6}\ln T_{i}\sum\limits_{i=1}^{6}y_{i}}{6}}{ \sum\limits_{i=1}^{6}y_{i}^{2}-\frac{\left( \sum\limits_{i=1}^{6}y_{i}\right) ^{2}}{6}}} }[/math]
- [math]\displaystyle{ \hat{b} =\frac{-8.0699-(23.9068)(-3.0070)/6}{7.1502-(-3.0070)^{2}/6} }[/math]
or:
- [math]\displaystyle{ \hat{b}=0.6931 }[/math]
and:
- [math]\displaystyle{ \hat{a}=\overline{x}-\hat{b}\overline{y}=\frac{\sum\limits_{i=1}^{6}\ln T_{i} }{6}-\hat{b}\frac{\sum\limits_{i=1}^{6}y_{i}}{6} }[/math]
or:
- [math]\displaystyle{ \hat{a}=\frac{23.9068}{6}-(0.6931)\frac{(-3.0070)}{6}=4.3318 }[/math]
Therefore, from Eqn. (EQNREF bwx ):
- [math]\displaystyle{ \hat{\beta }=\frac{1}{\hat{b}}=\frac{1}{0.6931}=1.4428 }[/math]
and from Eqn. (EQNREF awx )
- [math]\displaystyle{ \hat{\eta }=e^{\frac{\hat{a}}{\hat{b}}\cdot \frac{1}{\hat{ \beta }}}=e^{\frac{4.3318}{0.6931}\cdot \frac{1}{1.4428}}=76.0811\text{ hr} }[/math]
The correlation coefficient is found using Eqn. (EQNREF RHOw ):
- [math]\displaystyle{ \hat{\rho }=0.9956 }[/math]
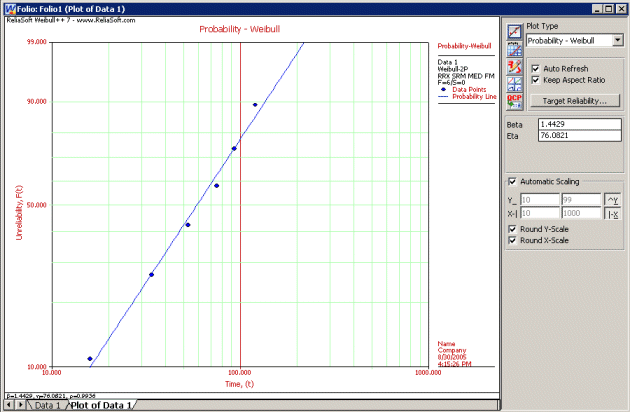
The results and the associated graph using Weibull++ are given next. Note that the slight variation in the results is due to the number of significant figures used in the estimation of the median ranks. Weibull++ by default uses double precision accuracy when computing the median ranks.
Three-Parameter Weibull Regression
When the MR versus Tj points plotted on the Weibull probability paper do not fall on a satisfactory straight line and the points fall on a curve,(Note that other shapes, particularly shapes, might suggest the existence of more than one population. In these cases, the multiple population, mixed Weibull distribution, may be more appropriate. Chapter 10 presents the mixed Weibull distribution.) then a location parameter, γ, might exist which may straighten out these points. The goal in this case is to fit a curve, instead of a line, through the data points using nonlinear regression. The Gauss-Newton method can be used to solve for the parameters, β, η and γ, by performing a Taylor series expansion on F(Ti;β,η,γ). Then the nonlinear model is approximated with linear terms and ordinary least squares are employed to estimate the parameters. This procedure is iterated until a satisfactory solution is reached. Weibull++ 7 calculates the value of γ by utilizing an optimized Nelder-Mead algorithm, and adjusts the points by this value of γ such that they fall on a straight line, and then plots both the adjusted and the original unadjusted points. To draw a curve through the original unadjusted points, if so desired, select Weibull 3P Line Unadjusted for Gamma from the Show Plot Line submenu under the Plot Options menu. The returned estimations of the parameters are the same when selecting RRX or RRY. To display the unadjusted data points and line along with the adjusted data points and line, select Show/Hide Items under the Plot Options menu and include the unadjusted data points and line as follows:
The results and the associated graph for the previous example using the three-parameter Weibull case are shown next:
Maximum Likelihood Estimation
As outlined in Chapter 3, maximum likelihood estimation works by developing a likelihood function based on the available data and finding the values of the parameter estimates that maximize the likelihood function. This can be achieved by using iterative methods to determine the parameter estimate values that maximize the likelihood function, but this can be rather difficult and time-consuming, particularly when dealing with the three-parameter distribution. Another method of finding the parameter estimates involves taking the partial derivatives of the likelihood function with respect to the parameters, setting the resulting equations equal to zero and solving simultaneously to determine the values of the parameter estimates. ( Note that MLE asymptotic properties do not hold when estimating γ using MLE [27].) The log-likelihood functions and associated partial derivatives used to determine maximum likelihood estimates for the Weibull distribution are covered in Appendix C.
SUBSUBSECTION
Example 5
Repeat Example 1 using maximum likelihood estimation.
SUBSUBSECTION
Solution to Example 5
In this case, we have non-grouped data with no suspensions or intervals, i.e. complete data. The equations for the partial derivatives of the log-likelihood function are derived in Appendix C and given next:
[math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{6}{\beta } +\sum_{i=1}^{6}\ln \left( \frac{T_{i}}{\eta }\right) -\sum_{i=1}^{6}\left( \frac{T_{i}}{\eta }\right) ^{\beta }\ln \left( \frac{T_{i}}{\eta }\right) =0 }[/math]
and:
[math]\displaystyle{ \frac{\partial \Lambda }{\partial \eta }=\frac{-\beta }{\eta }\cdot 6+\frac{ \beta }{\eta }\sum\limits_{i=1}^{6}\left( \frac{T_{i}}{\eta }\right) ^{\beta }=0 }[/math]
Solving the above equations simultaneously we get:
[math]\displaystyle{ \hat{\beta }=1.933, }[/math] [math]\displaystyle{ \hat{\eta }=73.526 }[/math]
The variance/covariance matrix is found to be,
[math]\displaystyle{ \left[ \begin{array}{ccc} \hat{Var}\left( \hat{\beta }\right) =0.4211 & \hat{Cov}( \hat{\beta },\hat{\eta })=3.272 \\ \hat{Cov}(\hat{\beta },\hat{\eta })=3.272 & \hat{Var} \left( \hat{\eta }\right) =266.646 \end{array} \right] }[/math]
The results and the associated graph using Weibull++ (MLE) are shown next.
You can view the variance/covariance matrix directly by clicking the Quick Calculation Pad (QCP) icon
FIGURE HERE
and then clicking the Show Fisher Matrix button on the Confidence Bounds tab of the QCP.
Note that the decimal accuracy displayed and used is based on your individual User Setup.
Fisher Matrix Confidence Bounds
One of the methods used by the application in estimating the different types of confidence bounds for Weibull data, the Fisher matrix method, is presented in this section. The complete derivations were presented in detail (for a general function) in Chapter 5.
Bounds on the Parameters
One of the properties of maximum likelihood estimators is that they are asymptotically normal, meaning that for large samples they are normally distributed. Additionally, since both the shape parameter estimate, [math]\displaystyle{ \hat{\beta } }[/math], and the scale parameter estimate, [math]\displaystyle{ \hat{\eta }, }[/math] must be positive, thus lnβ and lnη are treated as being normally distributed as well. The lower and upper bounds on the parameters are estimated from [30]:
[math]\displaystyle{ \beta _{U} =\hat{\beta }\cdot e^{\frac{K_{\alpha }\sqrt{Var(\hat{ \beta })}}{\hat{\beta }}}\text{ (upper bound)} }[/math]
[math]\displaystyle{ \beta _{L} =\frac{\hat{\beta }}{e^{\frac{K_{\alpha }\sqrt{Var(\hat{ \beta })}}{\hat{\beta }}}} \text{ (lower bound)} }[/math]
and:
[math]\displaystyle{ \eta _{U} =\hat{\eta }\cdot e^{\frac{K_{\alpha }\sqrt{Var(\hat{ \eta })}}{\hat{\eta }}}\text{ (upper bound)} }[/math]
[math]\displaystyle{ \eta _{L} =\frac{\hat{\eta }}{e^{\frac{K_{\alpha }\sqrt{Var(\hat{ \eta })}}{\hat{\eta }}}}\text{ (lower bound)} }[/math]
where [math]\displaystyle{ K_{\alpha} }[/math] is defined by:
[math]\displaystyle{ \alpha =\frac{1}{\sqrt{2\pi }}\int_{K_{\alpha }}^{\infty }e^{-\frac{t^{2}}{2} }dt=1-\Phi (K_{\alpha }) }[/math]
If δ is the confidence level, then [math]\displaystyle{ \alpha =\frac{1-\delta }{2} }[/math] for the two-sided bounds and α = 1 − δ for the one-sided bounds. The variances and covariances of [math]\displaystyle{ \hat{\beta } }[/math] and [math]\displaystyle{ \hat{\eta } }[/math] are estimated from the inverse local Fisher matrix, as follows:
[math]\displaystyle{ \left( \begin{array}{cc} \hat{Var}\left( \hat{\beta }\right) & \hat{Cov}\left( \hat{ \beta },\hat{\eta }\right)
\\
\hat{Cov}\left( \hat{\beta },\hat{\eta }\right) & \hat{Var} \left( \hat{\eta }\right) \end{array} \right) =\left( \begin{array}{cc} -\frac{\partial ^{2}\Lambda }{\partial \beta ^{2}} & -\frac{\partial ^{2}\Lambda }{\partial \beta \partial \eta }
\\
-\frac{\partial ^{2}\Lambda }{\partial \beta \partial \eta } & -\frac{ \partial ^{2}\Lambda }{\partial \eta ^{2}} \end{array} \right) _{\beta =\hat{\beta },\text{ }\eta =\hat{\eta }}^{-1} }[/math]
Fisher Matrix Confidence Bounds and Regression Analysis
Note that the variance and covariance of the parameters are obtained from the inverse Fisher information matrix as described in this section. The local Fisher information matrix is obtained from the second partials of the likelihood function, by substituting the solved parameter estimates into the particular functions. This method is based on maximum likelihood theory and is derived from the fact that the parameter estimates were computed using maximum likelihood estimation methods. When one uses least squares or regression analysis for the parameter estimates, this methodology is theoretically then not applicable. However, if one assumes that the variance and covariance of the parameters will be similar ( One also assumes similar properties for both estimators.) regardless of the underlying solution method, then the above methodology can also be used in regression analysis.
The Fisher matrix is one of the methodologies that Weibull++ uses for both MLE and regression analysis. Specifically, Weibull++ uses the likelihood function and computes the local Fisher information matrix based on the estimates of the parameters and the current data. This gives consistent confidence bounds regardless of the underlying method of solution, i.e. MLE or regression. In addition, Weibull++ checks this assumption and proceeds with it if it considers it to be acceptable. In some instances, Weibull++ will prompt you with an "Unable to Compute Confidence Bounds" message when using regression analysis. This is an indication that these assumptions were violated.
Bounds on Reliability
The bounds on reliability can easily be derived by first looking at the general extreme value distribution (EVD). Its reliability function is given by:
[math]\displaystyle{ R(t)=e^{-e^{\left( \frac{t-p_{1}}{p_{2}}\right) }} }[/math]
By transforming t = lnT and converting [math]\displaystyle{ p=\ln{\eta} }[/math], [math]\displaystyle{ p_{2}=\frac{1}{ \beta } }[/math], the above equation becomes the Weibull reliability function:
[math]\displaystyle{ R(T)=e^{-e^{\beta \left( \ln T-\ln \eta \right) }}=e^{-e^{\ln \left( \frac{T }{\eta }\right) ^{\beta }}}=e^{-\left( \frac{T}{\eta }\right) ^{\beta }} }[/math] With:
[math]\displaystyle{ R(T)=e^{-e^{\beta \left( \ln T-\ln \eta \right) }} EQNREF eq27 }[/math]
set [math]\displaystyle{ u=\beta \left( \ln T-\ln \eta \right). }[/math] The reliability function now becomes:
[math]\displaystyle{ R(T)=e^{-e^{u}} }[/math]
The next step is to find the upper and lower bounds on u. Using the equations derived in Chapter 5, the bounds on are then estimated from [30]:
[math]\displaystyle{ u_{U} =\hat{u}+K_{\alpha }\sqrt{Var(\hat{u})} }[/math]
[math]\displaystyle{ u_{L} =\hat{u}-K_{\alpha }\sqrt{Var(\hat{u})} }[/math]
where:
[math]\displaystyle{ Var(\hat{u}) =\left( \frac{\partial u}{\partial \beta }\right) ^{2}Var( \hat{\beta })+\left( \frac{\partial u}{\partial \eta }\right) ^{2}Var( \hat{\eta }) +2\left( \frac{\partial u}{\partial \beta }\right) \left( \frac{\partial u }{\partial \eta }\right) Cov\left( \hat{\beta },\hat{\eta }\right) }[/math]
or:
[math]\displaystyle{ Var(\hat{u}) =\frac{\hat{u}^{2}}{\hat{\beta }^{2}}Var(\hat{ \beta })+\frac{\hat{\beta }^{2}}{\hat{\eta }^{2}}Var(\hat{\eta }) -\left( \frac{2u}{\hat{\eta }}\right) Cov\left( \hat{\beta }, \hat{\eta }\right). EQNREF eq32 }[/math]
The upper and lower bounds on reliability are:
[math]\displaystyle{ R_{U} =e^{-e^{u_{L}}}\text{ (upper bound)} }[/math]
[math]\displaystyle{ R_{L} =e^{-e^{u_{U}}}\text{ (lower bound)} }[/math]
Other Weibull Forms
Weibull++ makes the following assumptions/substitutions in Eqn. (EQNREF eq27 ) to Eqn. (EQNREF eq32 ) when using the three-parameter or one-parameter forms:
- For the three-parameter case, substitute [math]\displaystyle{ t=\ln (T-\hat{\gamma }) }[/math] (and by definition γ < T), instead of lnT. (Note that this is an approximation since it eliminates the third parameter and assumes that [math]\displaystyle{ Var( \hat{\gamma })=0. }[/math])
- For the one-parameter, [math]\displaystyle{ Var(\hat{\beta })=0, }[/math] thus:
[math]\displaystyle{ Var(\hat{u})=\left( \frac{\partial u}{\partial \eta }\right) ^{2}Var( \hat{\eta })=\left( \frac{\hat{\beta }}{\hat{\eta }}\right) ^{2}Var(\hat{\eta }) }[/math]
Also note that the time axis (x-axis) in the three-parameter Weibull plot in Weibull++ 7 is not but T − γ. This means that one must be cautious when obtaining confidence bounds from the plot. If one desires to estimate the confidence bounds on reliability for a given time T0 from the adjusted plotted line, then these bounds should be obtained for a T0 − γ entry on the time axis.
Bounds on Time
The bounds around the time estimate or reliable life estimate, for a given Weibull percentile (unreliability), are estimated by first solving the reliability equation with respect to time, as follows [24, 30]:
[math]\displaystyle{ \ln R =-\left( \frac{T}{\eta }\right) ^{\beta } }[/math]
[math]\displaystyle{ \ln (-\ln R) =\beta \ln \left( \frac{T}{\eta }\right) }[/math]
[math]\displaystyle{ \ln (-\ln R) =\beta (\ln T-\ln \eta ) }[/math]
or:
[math]\displaystyle{ u=\frac{1}{\beta }\ln (-\ln R)+\ln \eta }[/math]
where u = lnT.
The upper and lower bounds on are estimated from:
[math]\displaystyle{ u_{U} =\hat{u}+K_{\alpha }\sqrt{Var(\hat{u})} }[/math]
[math]\displaystyle{ u_{L} =\hat{u}-K_{\alpha }\sqrt{Var(\hat{u})} }[/math]
where:
[math]\displaystyle{ Var(\hat{u})=\left( \frac{\partial u}{\partial \beta }\right) ^{2}Var( \hat{\beta })+\left( \frac{\partial u}{\partial \eta }\right) ^{2}Var( \hat{\eta })+2\left( \frac{\partial u}{\partial \beta }\right) \left( \frac{\partial u}{\partial \eta }\right) Cov\left( \hat{\beta },\hat{ \eta }\right) }[/math]
or: [math]\displaystyle{ Var(\hat{u}) =\frac{1}{\hat{\beta }^{4}}\left[ \ln (-\ln R)\right] ^{2}Var(\hat{\beta })+\frac{1}{\hat{\eta }^{2}}Var(\hat{\eta })+2\left( -\frac{1}{\hat{\beta }^{2}}\right) \left( \frac{\ln (-\ln R)}{ \hat{\eta }}\right) Cov\left( \hat{\beta },\hat{\eta }\right) }[/math]
The upper and lower bounds are then found by:
[math]\displaystyle{ T_{U} =e^{u_{U}}\text{ (upper bound)} }[/math]
[math]\displaystyle{ T_{L} =e^{u_{L}}\text{ (lower bound)} }[/math]
Likelihood Ratio Confidence Bounds
As covered in Chapter 5, the likelihood confidence bounds are calculated by finding values for θ1 and θ2 that satisfy:
[math]\displaystyle{ -2\cdot \text{ln}\left( \frac{L(\theta _{1},\theta _{2})}{L(\hat{\theta }_{1}, \hat{\theta }_{2})}\right) =\chi _{\alpha ;1}^{2} EQNREF lratio2 }[/math]
This equation can be rewritten as:
[math]\displaystyle{ L(\theta _{1},\theta _{2})=L(\hat{\theta }_{1},\hat{\theta } _{2})\cdot e^{\frac{-\chi _{\alpha ;1}^{2}}{2}} EQNREF lratio3 }[/math]
For complete data, the likelihood function for the Weibull distribution is given by:
[math]\displaystyle{ L(\beta ,\eta )=\prod_{i=1}^{N}f(x_{i};\beta ,\eta )=\prod_{i=1}^{N}\frac{ \beta }{\eta }\cdot \left( \frac{x_{i}}{\eta }\right) ^{\beta -1}\cdot e^{-\left( \frac{x_{i}}{\eta }\right) ^{\beta }} }[/math]
For a given value of α, values for β and η can be found which represent the maximum and minimum values that satisfy Eqn. (\ref {lratio3}). These represent the confidence bounds for the parameters at a confidence level δ, where α = δ for two-sided bounds and α = 2δ − 1 for one-sided.
Similarly, the bounds on time and reliability can be found by substituting the Weibull reliability equation into the likelihood function so that it is in terms of β and time or reliability, as discussed in Chapter 5. The likelihood ratio equation used to solve for bounds on time (Type 1) is:
[math]\displaystyle{ L(\beta ,t)=\prod_{i=1}^{N}\frac{\beta }{\left( \frac{t}{(-\text{ln}(R))^{ \frac{1}{\beta }}}\right) }\cdot \left( \frac{x_{i}}{\left( \frac{t}{(-\text{ ln}(R))^{\frac{1}{\beta }}}\right) }\right) ^{\beta -1}\cdot \text{exp}\left[ -\left( \frac{x_{i}}{\left( \frac{t}{(-\text{ln}(R))^{\frac{1}{\beta }}} \right) }\right) ^{\beta }\right] }[/math]
The likelihood ratio equation used to solve for bounds on reliability (Type 2) is:
[math]\displaystyle{ L(\beta ,R)=\prod_{i=1}^{N}\frac{\beta }{\left( \frac{t}{(-\text{ln}(R))^{ \frac{1}{\beta }}}\right) }\cdot \left( \frac{x_{i}}{\left( \frac{t}{(-\text{ ln}(R))^{\frac{1}{\beta }}}\right) }\right) ^{\beta -1}\cdot \text{exp}\left[ -\left( \frac{x_{i}}{\left( \frac{t}{(-\text{ln}(R))^{\frac{1}{\beta }}} \right) }\right) ^{\beta }\right] }[/math]
Bayesian Confidence Bounds
Bounds on Parameters
Bayesian Bounds use non-informative prior distributions for both parameters. From Chapter 5, we know that if the prior distribution of η and β are independent, the posterior joint distribution of η and β can be written as:
[math]\displaystyle{ f(\eta ,\beta |Data)= \dfrac{L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )}{\int_{0}^{\infty }\int_{0}^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
The marginal distribution of η is:
[math]\displaystyle{ f(\eta |Data) =\int_{0}^{\infty }f(\eta ,\beta |Data)d\beta = \dfrac{\int_{0}^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\beta }{\int_{0}^{\infty }\int_{-\infty }^{\infty }L(Data|\eta ,\beta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
where: [math]\displaystyle{ \varphi (\beta )=\frac{1}{\beta } }[/math] is the non-informative prior of β. [math]\displaystyle{ \varphi (\eta )=\frac{1}{\eta } }[/math] is the non-informative prior of η. Using these non-informative prior distributions, [math]\displaystyle{ f(\eta|Data) }[/math] can be rewritten as:
[math]\displaystyle{ f(\eta |Data)=\dfrac{\int_{0}^{\infty }L(Data|\eta ,\beta )\frac{1}{\beta } \frac{1}{\eta }d\beta }{\int_{0}^{\infty }\int_{0}^{\infty }L(Data|\eta ,\beta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } }[/math]
The one-sided upper bounds of η is:
[math]\displaystyle{ CL=P(\eta \leq \eta _{U})=\int_{0}^{\eta _{U}}f(\eta |Data)d\eta }[/math]
The one-sided lower bounds of η is:
[math]\displaystyle{ 1-CL=P(\eta \leq \eta _{L})=\int_{0}^{\eta _{L}}f(\eta |Data)d\eta }[/math] The two-sided bounds of η is:
[math]\displaystyle{ CL=P(\eta _{L}\leq \eta \leq \eta _{U})=\int_{\eta _{L}}^{\eta _{U}}f(\eta |Data)d\eta }[/math] Same method is used to obtain the bounds of β.
Bounds on Time (Type 1)
From Chapter 5, we know that:
[math]\displaystyle{ CL=\Pr (T\leq T_{U})=\Pr (\eta \leq T_{U}\exp (-\frac{\ln (-\ln R)}{\beta })) }[/math] From the posterior distribution of η, we have:
[math]\displaystyle{ CL=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T_{U}\exp (-\dfrac{ \ln (-\ln R)}{\beta })}L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } EQNREF BayesCLT }[/math]
Eqn. (EQNREF BayesCLT ) is solved numerically for TU. The same method can be applied to calculate one sided lower bounds and two-sided bounds on time.
Bounds on Reliability (Type 2)
[math]\displaystyle{ CL=\Pr (R\leq R_{U})=\Pr (\eta \leq T\exp (-\frac{\ln (-\ln R_{U})}{\beta })) }[/math] From the posterior distribution of η, we have:
[math]\displaystyle{ CL=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T\exp (-\dfrac{\ln (-\ln R_{U})}{\beta })}L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\frac{1}{\beta }\frac{1}{\eta }d\eta d\beta } EQNREF BayesCLR }[/math]
Eqn. (EQNREF BayesCLR ) is solved numerically for RU. The same method can be used to calculate the one sided lower bounds and two-sided bounds on reliability.
Weibull-Bayesian Analysis
In this section, the Bayesian methods are presented for the two-parameter Weibull distribution. Bayesian concepts were introduced in Chapter 3. This model considers prior knowledge on the shape (β) parameter of the Weibull distribution when it is chosen to be fitted to a given set of data. There are many practical applications for this model, particularly when dealing with small sample sizes and some prior knowledge for the shape parameter is available. For example, when a test is performed, there is often a good understanding about the behavior of the failure mode under investigation, primarily through historical data. At the same time, most reliability tests are performed on a limited number of samples. Under these conditions, it would be very useful to use this prior knowledge with the goal of making more accurate predictions. A common approach for such scenarios is to use the one-parameter Weibull distribution, but this approach is too deterministic, too absolute you may say (and you would be right). The Weibull-Bayesian model in Weibull++ (which is actually a true "WeiBayes" model, unlike the one-parameter Weibull that is commonly referred to as such) offers an alternative to the one-parameter Weibull, by including the variation and uncertainty that might have been observed in the past on the shape parameter. Applying Bayes's rule on the two-parameter Weibull distribution and assuming the prior distributions of β and η are independent, we obtain the following posterior :
[math]\displaystyle{ f(\beta ,\eta |Data)=\dfrac{L(\beta ,\eta )\varphi (\beta )\varphi (\eta )}{ \int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta } }[/math] EQNREF WeibBayes
In this model, η is assumed to follow a noninformative prior distribution with the density function [math]\displaystyle{ \varphi (\eta )=\dfrac{1}{\eta } }[/math]. This is called Jeffrey's prior, and is obtained by performing a logarithmic transformation on η. Specifically, since η is always positive, we can assume that ln(η) follows a uniform distribution, U( − ∞, + ∞). Applying Jeffrey's rule [9] which says "in general, an approximate non-informative prior is taken proportional to the square root of Fisher's information", yields [math]\displaystyle{ \varphi (\eta )=\dfrac{1}{\eta }. }[/math]
The prior distribution of β, denoted as [math]\displaystyle{ \varphi (\beta ) }[/math], can be selected from the following distributions: normal, lognormal, exponential and uniform. The procedure of performing a Weibull-Bayesian analysis is as follows:
- Collect the times-to-failure data.
- Specify a prior distribution for β (the prior for η is assumed to be 1/η).
- Obtain the posterior from Eqn. (EQNREF WeibBayes ).
In other words, a distribution (the posterior ) is obtained, rather than a point estimate as in classical statistics (i.e., as in the parameter estimation methods described previously in this chapter). Therefore, if a point estimate needs to be reported, a point of the posterior needs to be calculated. Typical points of the posterior distribution used are the mean (expected value) or median. In Weibull++, both options are available and can be chosen from the Analysis page, under the Results As area, as shown next.
The expected value of β is obtained by:
[math]\displaystyle{ E(\beta )=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\beta \cdot f(\beta ,\eta |Data)d\beta d\eta }[/math]
Similarly, the expected value of η is obtained by:
[math]\displaystyle{ E(\eta )=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\eta \cdot f(\beta ,\eta |Data)d\beta d\eta }[/math]
The median points are obtained by solving the following equations for [math]\displaystyle{ \breve{\beta} }[/math] and [math]\displaystyle{ \breve{\eta} }[/math] respectively:
[math]\displaystyle{ \int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\breve{\beta}}f(\beta ,\eta |Data)d\beta d\eta =0.5 }[/math]
and
[math]\displaystyle{ \int\nolimits_{0}^{\breve{\eta}}\int\nolimits_{0}^{\infty }f(\beta ,\eta |Data)d\beta d\eta =0.5 }[/math]
Of course, other points of the posterior distribution can be calculated as well. For example, one may want to calculate the 10th percentile of the joint posterior distribution (w.r.t. one of the parameters). The procedure for obtaining other points of the posterior distribution is similar to the one for obtaining the median values, where instead of 0.5 the percentage of interest is given. This procedure actually provides the confidence bounds on the parameters, which in the Bayesian framework are called ‘‘Credible Bounds‘‘. However, since the engineering interpretation is the same, and to avoid confusion, we refer to them as confidence bounds in this reference and in Weibull++.
Posterior Distributions for Functions of Parameters
As explained in Chapter 3, in Bayesian analysis, all the functions of the parameters are distributed. In other words, a posterior distribution is obtained for functions such as reliability and failure rate, instead of point estimate as in classical statistics. Therefore, in order to obtain a point estimate for these functions, a point on the posterior distributions needs to be calculated. Again, the expected value (mean) or median value are used.
[math]\displaystyle{ pdf }[/math] of the Times-to-Failure
The posterior distribution of the failure time is given by:
[math]\displaystyle{ f(T|Data)=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }f(T,\beta ,\eta )f(\beta ,\eta |Data)d\eta d\beta }[/math] EQNREF WeibBayesPDF
where:
[math]\displaystyle{ f(T,\beta ,\eta )=\dfrac{\beta }{\eta }\left( \dfrac{T}{\eta }\right) ^{\beta -1}e^{-\left( \dfrac{T}{\eta }\right) ^{\beta }} }[/math]
For the [math]\displaystyle{ pdf }[/math] of the times-to-failure, only the expected value is calculated and reported in Weibull++.
Reliability
In order to calculate the median value of the reliability function, we first need to obtain posterior of the reliability. Since R(T) is a function of β, the density functions of β and R(T) have the following relationship:
[math]\displaystyle{ \begin{align} f(R|Data,T)dR = & f(\beta |Data)d\beta)\\ = & (\int\nolimits_{0}^{\infty }f(\beta ,\eta |Data)d{\eta}) d{\beta} \\ =& \dfrac{\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }d\beta \end{align} }[/math] EQNREF Rpdf
The median value of the reliability is obtained by solving the following equation w.r.t. [math]\displaystyle{ \breve{R}: }[/math]
[math]\displaystyle{ \int\nolimits_{0}^{\breve{R}}f(R|Data,T)dR=0.5 }[/math] EQNREF MedRel
The expected value of the reliability at time is given by:
[math]\displaystyle{ R(T|Data)=\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }R(T,\beta ,\eta )f(\beta ,\eta |Data)d\eta d\beta }[/math] where:
[math]\displaystyle{ R(T,\beta ,\eta )=e^{-\left( \dfrac{T}{\eta }\right) ^{^{\beta }}} }[/math]
Failure Rate
The failure rate at time is given by:
[math]\displaystyle{ \lambda (T|Data)=\dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }\lambda (T,\beta ,\eta )L(\beta ,\eta )\varphi (\eta )\varphi (\beta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\eta )\varphi (\beta )d\eta d\beta } }[/math]
where:
[math]\displaystyle{ \lambda (T,\beta ,\eta )=\dfrac{\beta }{\eta }\left( \dfrac{T}{\eta }\right) ^{\beta -1} }[/math]
Note on Calculated Results
As mentioned above, in order to obtain point estimates for the parameters of functions of the parameters in Bayesian analysis, the Median or Mean values of the different posterior [math]\displaystyle{ pdf }[/math]s are calculated. It is important to note that the Median value is preferable and is the default in Weibull++. This is because the Median value always corresponds to the 50th percentile of the distribution. On the other hand, the Mean is not a fixed point on the distribution, which could cause issues, especially when comparing results across different data sets.
Confidence Bounds on R(T)
The confidence bounds calculation under the Weibull-Bayesian analysis is very similar to the Bayesian Confidence Bounds method described in the previous section, with the exception that in the case of the Weibull-Bayesian Analysis the specified prior of β is considered instead of an non-informative prior. The Bayesian one-sided upper bound estimate for R(T) is given by:
[math]\displaystyle{ \int\nolimits_{0}^{R_{U}(T)}f(R|Data,T)dR=CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and (EQNREF Rpdf ) the following is obtained:
[math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{T\exp (-\dfrac{\ln (-\ln R_{U})}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLRU
Eqn. (EQNREF 1CLRU ) can be solved for RU(T). The Bayesian one-sided lower bound estimate for [math]\displaystyle{ \ R(T) }[/math] is given by:
[math]\displaystyle{ \int\nolimits_{0}^{R_{L}(T)}f(R|Data,T)dR=1-CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and (EQNREF Rpdf ) the following is obtained:
[math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T\exp (-\dfrac{\ln (-\ln R_{L})}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=1-CL }[/math] EQNREF 1CLRL
Eqn. (EQNREF 1CLRL ) can be solved for RL(T). The Bayesian two-sided bounds estimate for R(T) is given by:
[math]\displaystyle{ \int\nolimits_{R_{L}(T)}^{R_{U}(T)}f(R|Data,T)dR=CL }[/math] which is equivalent to:
[math]\displaystyle{ \int\nolimits_{0}^{R_{U}(T)}f(R|Data,T)dR=(1+CL)/2 }[/math]
and
[math]\displaystyle{ \int\nolimits_{0}^{R_{L}(T)}f(R|Data,T)dR=(1-CL)/2 }[/math]
Using the same method for one-sided bounds, RU(T)and RL(T) can be computed.
Confidence Bounds on Time
Following the same procedure described for bounds on Reliability, the bounds of time can be calculated, given . The Bayesian one-sided upper bound estimate for T(R) is given by:
[math]\displaystyle{ \int\nolimits_{0}^{T_{U}(R)}f(T|Data,R)dT=CL }[/math]
Using Eqns. (EQNREF WeibBayes ) and. (EQNREF WeibBayesPDF ), we obtain:
[math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{T_{U}\exp (-\dfrac{\ln (-\ln R)}{\beta })}L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLTU
Eqn. (EQNREF 1CLTU ) can be solved for TU(R). The Bayesian one-sided lower bound estimate for T(R) is given by:
[math]\displaystyle{ \int\nolimits_{0}^{T_{L}(R)}f(T|Data,R)dT=1-CL }[/math]
or:
[math]\displaystyle{ \dfrac{\int\nolimits_{0}^{\infty }\int\nolimits_{T_{L}\exp (\dfrac{-\ln (-\ln R)}{\beta })}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }{\int\nolimits_{0}^{\infty }\int\nolimits_{0}^{\infty }L(\beta ,\eta )\varphi (\beta )\varphi (\eta )d\eta d\beta }=CL }[/math] EQNREF 1CLTL
Eqn. (EQNREF 1CLTL ) can be solved for TL(R). The Bayesian two-sided lower bounds estimate for T(R) is:
[math]\displaystyle{ \int\nolimits_{T_{L}(R)}^{T_{U}(R)}f(T|Data,R)dT=CL }[/math]
which is equivalent to:
[math]\displaystyle{ \int\nolimits_{0}^{T_{U}(R)}f(T|Data,R)dT=(1+CL)/2 }[/math]
and:
[math]\displaystyle{ \int\nolimits_{0}^{T_{L}(R)}f(T|Data,R)dT=(1-CL)/2 }[/math]
Example 6
A manufacturer has tested prototypes of a modified product. The test was terminated at 2000 hours, with only two failures observed from a sample size of eighteen.
| Number of State | State of F or S | State End Time |
| 1 | F | 1180 |
| 1 | F | 1842 |
| 16 | S | 2000 |
Because of the lack of failure data in the prototype testing, the manufacturer decided to use information gathered from prior tests on this product to increase the confidence in the results of the prototype testing. This decision was made because failure analysis indicated that the failure mode of these two failures is the same as the one observed in previous tests. In other words, it is expected that the shape of the distribution hasn't changed, but hopefully the scale has, indicating longer life. The two-parameter Weibull distribution have been used to model all prior tests results. The list of the estimated β parameter is as follows:
| Betas Obtained for Similar Mode |
| 1.7 |
| 2.1 |
| 2.4 |
| 3.1 |
| 3.5 |
First, in order to fit the data to a Weibull-Bayesian model, a prior distribution for β needs to be determined. Based on the prior tests' β values, the prior distribution for β was found to be a lognormal distribution with μ = 0.9064, σ = 0.3325 (obtained by entering the β values into a Weibull++ Standard Folio and analyzing it based on the RRX analysis method.)
the test data is entered into a Standard Folio, the Weibull-Bayesian is selected under Distribution and the β prior distribution is entered after clicking the Calculate button.
Suppose that the reliability at 3000hr is the metric of interest in this example. This reliability can be obtained using Eqn. (EQNREF MedRel ), resulting in the median value of the posterior of the reliability at 3000hr. Using the QCP, this value is calculated to be 76.97. ( By default Weibull++ returns the median values of the posterior distribution. )
The posterior [math]\displaystyle{ pdf }[/math] of the reliability function at 3000hrs can be obtained using Eqn. (EQNREF Rpdf ). In Figure 6-10 the posterior [math]\displaystyle{ pdf }[/math] of the reliability at 3000hrs is plotted, with the corresponding median value as well as the 10th percentile value shown. The 10th percentile constitutes the 90 Lower 1-Sided bound on the reliability at 3000hrs, which is calculated to be 50.77.
FIGURE HERE
Notice that the [math]\displaystyle{ pdf }[/math] plotted in Fig. 6-10 is of the reliability at 3000hrs, and not the [math]\displaystyle{ pdf }[/math] of the times-to-failure data. The [math]\displaystyle{ pdf }[/math] of the times-to-failure data can be obtained using Eqn. (EQNREF WeibBayesPDF ) and plotted using Weibull++, as shown next:
FIGURE HERE
| The material on this page is copyrighted. | ©1992-2012. ReliaSoft Corporation. ALL RIGHTS RESERVED. |